波浪滑翔机椭圆形后缘水翼动力特性研究

王兵振，周茜子，刘 政,2，王 鑫，马 勇

（1. 国家海洋技术中心，天津 300112；2. 天津大学，天津 300072；3. 南方海洋科学与工程广东省实验室（珠海）， 广东 珠海 519080）

波浪滑翔机是一种新型的无人海上移动观测平台。通过水翼，波浪滑翔机将波浪能量直接转换为向前推进的机械能，实现海上移动，极大节省电力能源[1]。基于水面母船上100～150 W太阳能电池板的发电单元，及锂电池组构成的蓄能单元，波浪滑翔机设置了小型光伏供电模块，为控制系统、通讯系统、传感器和其他海洋观测设备提供电能[2]。在充分利用可再生能源的基础上，波浪滑翔机可实现长达数月的海上连续工作，具有成本相对较低、续航能力长、对环境友好、隐蔽能力高等特点，在海洋水文观测[3]、生物学研究[4]、海洋环境监测[5-6]等许多海洋研究领域被广泛应用。

水翼是波浪滑翔机中将波浪能转化为前进动力的关键部件，直接决定波浪滑翔机的动力特性。目前，国内外已开展了大量的波浪滑翔机水翼动力特性相关研究。KRAUS N D[7]研究提出了波浪滑翔机六个自由度非线性动力学分析模型，分析对象的水翼翼型为NACA0009，水翼的弦长为0.17 m，展弦比为3.36。刘鹏等[8-9]采用二维串联异步扑翼的理论模型，研究了基于NACA0012翼型、弦长为160 mm、展弦比为3.375的波浪滑翔翼的水动力性能。周春林等[10]对波浪滑翔机的动力特性进行了仿真研究，研究对象的水翼为平板翼，厚度为1 mm，展弦比为2.14。基于NACA0012翼型，YANG F等[11]研究了波浪滑翔机的动态性能数值预测模型，其分析对象的水翼长度为160 mm，展弦比为3.75，水翼的平面形状为矩形。基于NACA0012翼型， 卢旭[12]开发了一种波浪滑翔机，建立了波浪滑翔机动力学分析模型，分析了海上的风、浪等各种因素对于波浪滑翔机运动的干扰以及滑翔机的控制性能，其研究对象的水翼展弦比为5。对于不同翼型对水翼动力特性的影响，DING N P[13]采用CFD方法对比分析了平板翼和基于NACA0012翼型的两种水翼的动力特性，研究对象的展弦比为5。吴世其等[14]通过FLUENT软件进行仿真模拟，研究了在不同海况下水翼的翼板间距以及转轴位置的变化对产生的推力的影响，为水翼的设计提供了参考。胡峰等[15]通过Star-CCM+软件中的平面运动机构模块，对水翼的耦合运动进行模拟仿真，分析了波浪要素和水翼的结构参数等对水翼的推进性能的影响。 周润婕等[16]制作了波浪滑翔机的水下牵引机缩尺模型，分析了不同情况下的水翼性能。

对于波浪滑翔机水翼，断面形状、平面形状和展弦比是决定水翼动力特性的最为关键的3个因素。目前，国内外波浪滑翔机水翼的相关研究中，对水翼的断面形状（即翼型）的研究较多，且主要集中在NACA0012和平板翼2种翼型。对于水翼的平面形状来说，研制的波浪滑翔机的水翼主要采用矩形平面外形，水翼长度在600～700 mm之间，展弦比在3.36～5之间；有少数对水翼的前缘或后缘稍微采用圆弧处理，但系统性的理论研究还未开展。针对水翼设计问题，本文提出了一种具有椭圆后缘的水翼设计方案，对比分析了椭圆后缘水翼与平直水翼的动力特性，并根据动力学仿真分析结果，给出了一些关于水翼优化设计的建议。

1 计算模型及验证

利用计算流体力学(Computational Fluid Dynamics，CFD)方法，对波浪滑翔机水翼的动力特性进行了仿真分析。为了验证计算模型的合理性，建立了NACA0012翼型升力系数分析模型，并与文献的测试结果进行了对比[17-18]。由于波浪滑翔机的运动速度相对较低，在实际工作过程中水翼运动的雷诺数较低，因此在升力系数的对比分析过程中，选择了小雷诺数的工作条件。计算模型中翼型的弦长为1 m，工作介质为空气，入口流速分别为1.8 m/s和0.45 m/s，相应的雷诺数分别为0.5×106和2×106。在流体数值计算中，边界层区域的网格划分质量对于提高计算精度至关重要[19]；对翼型附近区域的网格采用层状网格进行加密处理，第1层的厚度为0.1 mm。翼型区域的网格划分情况如图1所示。

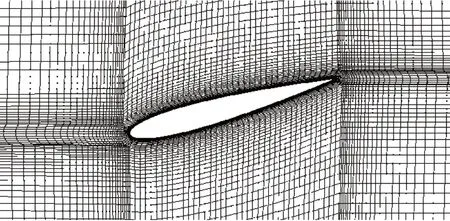
图1 NACA0012模型网格

NACA0012翼型升力系数的计算结果如图2所示。图中，横轴为翼型的运动攻角，纵轴为翼型的升力系数。由图2可知，当攻角小于12°时，计算出的升力系数与试验结果吻合情况较好，但当攻角大于12°时，计算的升力系数与文献的试验结果出现了一定的偏差；另外，雷诺数对模型的计算精度存在一定的影响，对比攻角为6°、12°两个位置的升力系数，雷诺数为2.0×106条件下的CL计算误差明显小于雷诺数为0.5×106的情况，说明雷诺数的增大对于提高模型的计算精度有利。

图2 NACA0012翼型升力系数

1.1 展弦比对水翼动力特性的影响

基于CFD方法，考察了两种不同展弦比的平板翼的升力特性。2种平板翼的截面形状为矩形，厚度均为6.0 mm。为便于对比，两种水翼的平面投影面积相同，弦长分别为156.0 mm和134.0 mm，长度分别为600.0 mm和700.0 mm。两种平板翼的展弦比分别为3.85和5.22。计算对象为有限长平板水翼，动力特性计算中需要考虑边部效应的影响，计算模型的网格划分情况如图3所示。

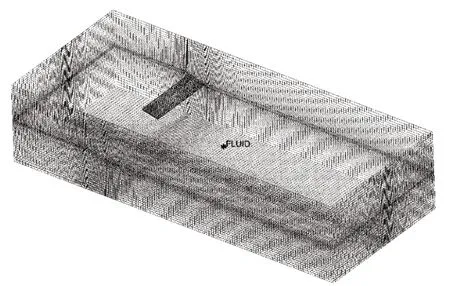
图3 有限长水翼模型网格图

在运动过程中，波浪滑翔机水面母船在波浪作用下产生升降运动，带动水翼在水下作上下浮沉运动，同时由于波浪的推力，波浪滑翔机会做水平向前运动。因此，水翼的绝对速度是水平方向和垂直方向的矢量和。波浪滑翔机在3级海况（有效波高0.5～1.25 m）条件下的速度约为0.5 m/s[20]，这个海况下波浪的平均周期约为3 s；波浪滑翔机在波浪作用下的升降频率与波周期接近，因此升降的平均速度约为0.4 m/s，考虑到升降过程中速度有变化的因素，因此假定升降的速度为0.5 m/s。而母船和水翼的升降速度与水平运动速度接近。因此，假定水翼相对海水的运动速度为0.7 m/s，水翼运动的雷诺数约为

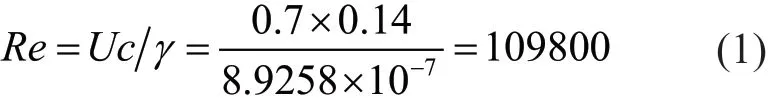
式中：Re为雷诺数；U为来流速度，m/s；c为弦长，m；γ为水的运动粘度，取8.925 8×10-7，m/s2；弦长取前述弦长圆整后的中间值，m。

根据平板翼的CFD升力计算结果，可得有限长平板水翼的升力系数：

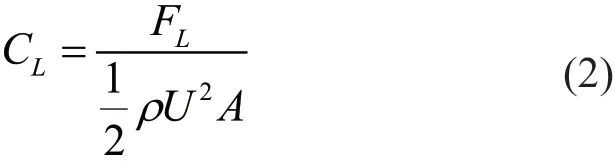
式中：CL为升力系数；FL为有限长水翼的升力，N；ρ为水的密度，kg/m3；U为来流速度，m/s；A为水翼的横截面积，m2。

两种不同展弦比平板水翼的升力系数的计算结果如图4所示。图中，横轴为水翼的运动攻角，纵轴为平板水翼的升力系数。由图4可知，两种平板水翼的升力系数非常接近；当攻角小于8°时，大展弦比水翼的升力系数略大于小展弦比水翼；而当攻角大于8°时，两种不同的展弦比的水翼的升力系数几乎相同。目前，国内外研制的波浪滑翔机的水翼的展弦比均在3.85～5.22范围内，属于中等展弦比机翼。在这个范围内，展弦比的变化对水翼的升力特性影响很小。

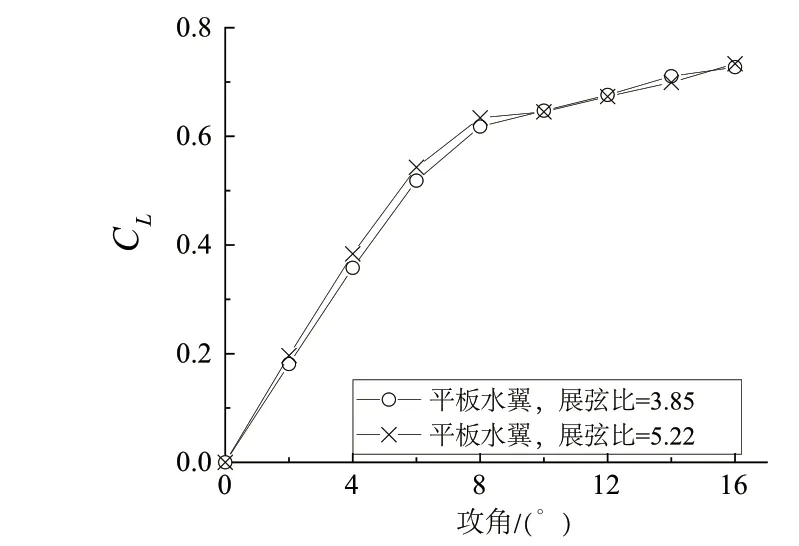
图4 不同展弦比的扁平水翼升力系数

1.2 翼型对水翼动力特性的影响

在波浪滑翔机水翼设计中，NACA0012和平板翼是应用最为广泛的两种翼型。基于NACA0012构建的水翼的断面形状为NACA0012翼型，而平板翼的断面形状为矩形。利用CFD分析方法，考察了两种翼型对波浪滑翔机水翼动力特性的影响。计算过程中水翼的雷诺数取1×105，计算模型中两种水翼除截面形状不同，其余物理性质均保持一致，长度为700 mm，弦长为134 mm，展弦比为5.22；水翼相对海水的运动速度为0.7 m/s。计算模型的网格划分情况与图3相近，在此不再重复。

两种不同截面水翼的升力系数计算结果如图5所示。由图可知，在小攻角的情况下，两种水翼的升力系数非常接近，且平板翼的升力系数略高于NACA0012水翼的升力系数；当攻角在8°～15°时，NACA0012型水翼的升力系数明显高于平板翼的升力系数；两种水翼的升力系数在10°攻角时相差最大，对应的NACA0012型水翼的升力系数达到最大值0.793 9，而平板翼对应的升力系数仅为0.645 2；当攻角接近16°时，两个水翼的升力系数再次变得接近。总体上来说，基于NACA0012构建的水翼的升力特性优于平板翼，在水翼设计中应优先选用NACA0012翼型。

图5 不同截面水翼的升力系数

1.3 平面形状对水翼动力特性的影响

1.3.1 平面形状控制方程 波浪滑翔机水翼的平面形状对水翼的动力特性有一定的影响。根据机翼理论，椭圆形机翼具有最佳的升力分布，可以大大减少诱导阻力，提高机翼的工作性能[21-22]。但由于制造的复杂性，单纯的椭圆形机翼很少使用，而是采用梯形机翼来代替椭圆机翼，以在降低制造难度的同时提高机翼动力性能。对于波浪滑翔机的水翼，拟同样对其平面形状进行椭圆化处理，提升其动力性能。水翼平面外形椭圆化处理的外形如图6所示。图中，水翼每一个纵剖面最大内切圆的中心在同一条直线上，用椭圆曲线代替平直水翼的部分后缘。水翼后缘的椭圆曲线方程如下:

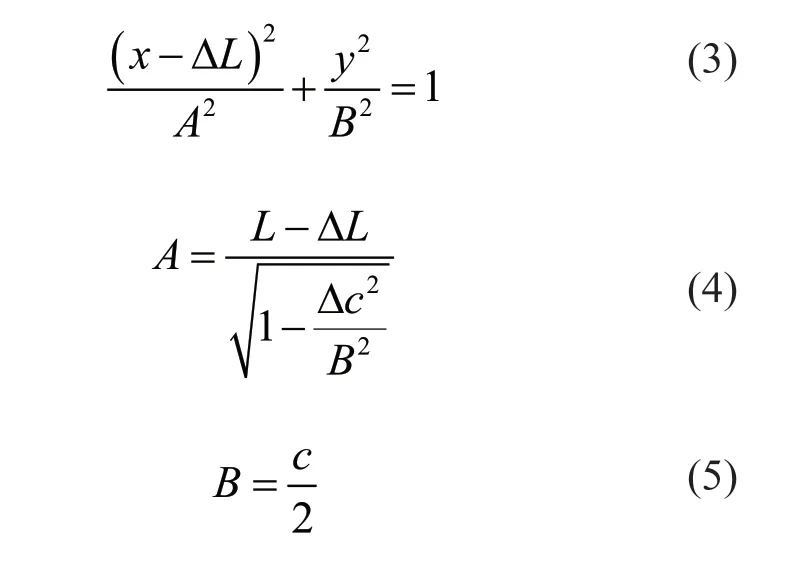
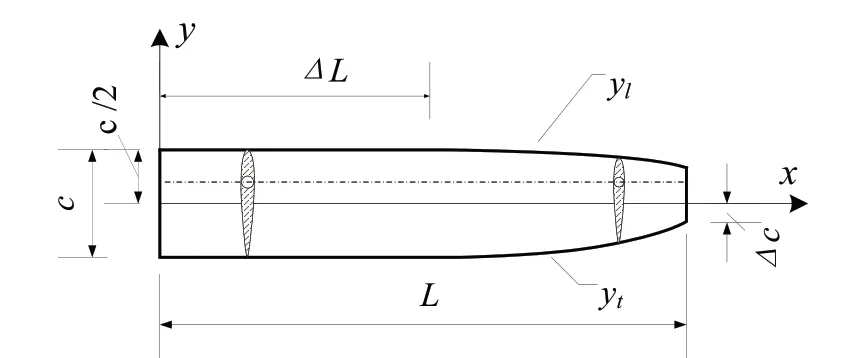
图6 椭圆尾缘水翼的平面形状

式中：ΔL为水翼后缘的直段长度，m；L为水翼后缘长度，m；c为水翼根弦长度，m；Δc是水翼尾缘最外点与x轴之间的距离，m。

为了确保水翼的所有断面保持完整的NACA0012外形，水翼的前缘也需要相应地进行修改。水翼椭圆前缘和椭圆后缘曲线部分的计算方法如下

式中：yt为水翼前缘曲线段各点的纵向坐标，m；yl为水翼后缘曲线段各点的纵向坐标，m。

1.3.2 不同平面形状水翼的动力特性 基于水翼平面形状控制方程，提出了一种具有椭圆后缘的水翼，其技术参数如表1所示。为便于与具有矩形平面外形的平直水翼相比较，将具有相同平面投影面积的平直水翼的参数也列在表1中，两种水翼的截面形状均为NACA0012。

表1 叶片参数

利用CFD计算方法，计算了具有不同平面外形的两种水翼的升力系数，计算结果如图7所示。由图可知，椭圆后缘水翼的升力性能略优于平直水翼。当水翼的攻角小于8°时，两种方案的升力系数几乎相同；而当攻角超过8°时，椭圆后缘水翼的升力优于平直水翼；在攻角为12°时，椭圆后缘水翼的升力系数最大值为0.835，比平直水翼的升力系数高7.5%。

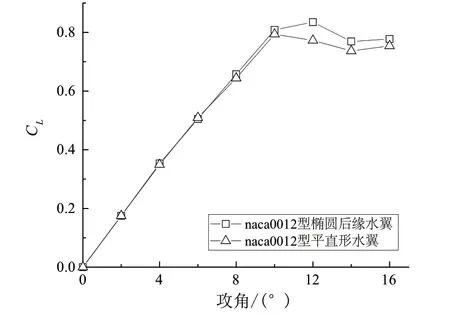
图7 不同平面形状水翼的升力系数

两种水翼的阻力特性的计算结果如图8所示。由图可知，在所研究的攻角范围内，两种水翼的阻力非常接近。当攻角小于10°时，椭圆后缘水翼的阻力略大于平直水翼；而当攻角大于10°时，椭圆后缘水翼的阻力略小于平直水翼。

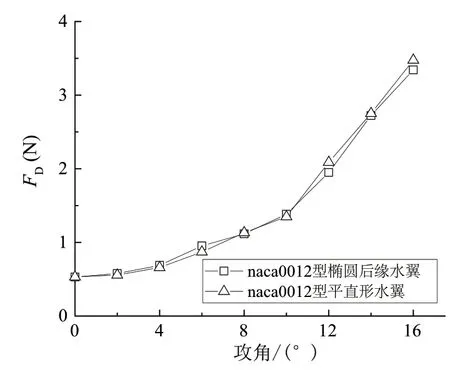
图8 不同平面形状水翼的阻力

2 阵列条件下椭圆后缘水翼特性

2.1 2D水翼阵列动力特性分析

波浪滑翔机通常有6对水翼，前后水翼边缘的距离相对较近。水翼的阵列化对水翼的动力特性有较大的影响。波浪滑翔机的母船在波浪的作用下上下起伏，波浪滑翔机的水下牵引机在母船拉力或自身重力作用下上升或下降。在上升运动的同时，水下牵引机的水翼产生水平推力，使波浪滑翔机向前移动。水翼阵列结构如图9所示。

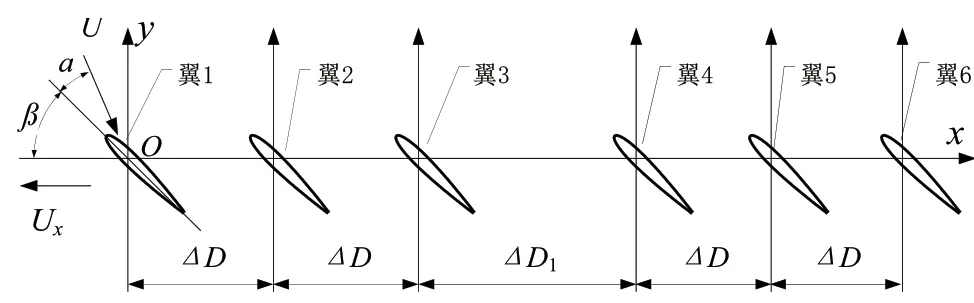
图9 水下牵引机上升时水翼阵列运动情况

水下牵引机的水翼分为两组。每组水翼有3对水翼，弦长为134 mm。同一组水翼中相邻两个水翼之间的距离为ΔD= 190 mm，前后两组水翼之间的距离为ΔD1= 440 mm。水下牵引机水翼的运动位置限位角为±30°。图9滑翔机的前进速度为Ux，水翼相对于水流的攻角为a。

基于水翼阵列的二维CFD计算模型，研究了阵列化对水翼动力特性的影响。为了简化计算，在CFD模型中将水翼阵列绕O点以逆时针方向旋转a+β的角度，使水翼相对海水的运动方向为水平方向。当水流速度U= 0.7 m/s，水翼的运动攻角a分别为4°、8°和12°时，阵列中各水翼的升力系数的计算结果如图10所示。为了便于对比分析，NACA0012 2D 翼型在相同雷诺数和攻角下的升力系数也绘制在图10中。

由图10可知，阵列化对水翼的动力特性有很大影响；水翼的运动攻角越大，阵列化的影响也越大。在攻角分别为4°和8°的情况下，翼1、翼2和翼4的升力系数均大于相同攻角的NACA0012翼形的升力系数；最后的水翼的升力系数则小于NACA0012翼形的升力系数；翼3和翼5的升力系数几乎等同于NACA0012翼形的升力系数。当攻角增加到12°时，只有最后面的水翼的升力系数接近NACA0012翼形的升力系数，其余五个水翼的升力系数明显高于NACA0012翼形。

图10 水翼的升力系数

对于同一组的三个水翼，前翼的升力系数大于后翼的升力系数。在研究的攻角范围内，前一组水翼中翼3的升力系数约为翼1的30%～50%，后面一组水翼中翼6的升力系数仅为翼4的40%～60%。

此外，前一组水翼的升力系数通常高于后面一组的升力系数。在攻角为4°、8°、12°时，后一组水翼的平均升力系数分别为前一组的73.2%、75.7%和89.7%。

对于水翼阵列，相邻的水翼会影响水翼周围的水粒子的运动，水流相对于水翼的方向将改变。这种变化增加了水翼相对于水流的攻角，从而增加了升力系数。当攻角等于12°时，水翼阵列的流场的流线如图11所示。由图11可知，水翼前面的流线不再保持水平，而是明显向下倾斜。特别是对于翼1和翼4，流线的下倾角相对较大，说明水翼前部的流动方向发生了较大的变化，从而对水翼的升力特性产生了较大的影响。

图11 水翼阵流场的流线图

2.2 阵列化条件下椭圆后缘水翼特性分析

阵列化对水翼的动力特性有较大的影响。本文建立了CFD分析模型，对比分析了阵列化条件下椭圆形后缘水翼和平直水翼间动力特性的差异。对比的对象为表1中给出的两种水翼，水翼的数量、布局和间距等阵列化参数与上述2D模型相同。当波浪滑翔机的水下牵引机向上运动且水翼位于30°极限位置时，椭圆形后缘水翼阵列计算模型如图12所示。

图12 椭圆形后缘水翼阵列计算模型

计算过程中，水翼的运动速度设定为0.7 m/s。在不同攻角下，水翼升力系数特性的计算结果如图13所示。为便于比较说明，将相同雷诺数和攻角条件下的单个椭圆形后缘水翼的升力系数也标示在图中。

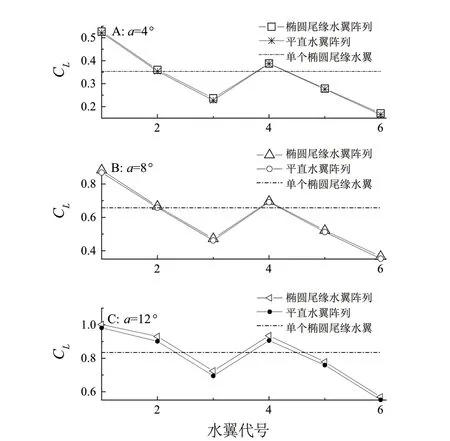
图13 不同攻角下水翼的升力系数

与二维分析结果相似，水翼阵列化对水翼的升力系数有很大影响。在攻角α= 4°和8°时，翼1和翼4的升力系数大于相同攻角的单个水翼的升力系数；翼3、翼5和翼6的升力系数小于单翼的升力系数；翼2的升力系数与单水翼的升力系数较为接近。但当攻角增加到12°时，翼1、翼2和翼4的升力系数明显大于单个水翼的升力系数，而其他三个水翼的升力系数小于单个水翼的升力系数。

对比分析两种不同平面形状的水翼的升力系数，在攻角a= 4°、8°时，两种水翼的升力系数基本相同。当攻角增加到12°时，具有椭圆尾缘的水翼的升力系数明显高于平直水翼，椭圆尾缘水翼的升力系数比平直水翼大约高2%～4% 。

利用CFD模型，计算了阵列化条件下两种水翼的阻力特性。计算过程中，流速仍为0.7 m/s。攻角分别为4°、8°和12°时，各水翼的阻力的计算结果如图14所示。对于翼1位置的水翼，带有椭圆后缘的水翼所受的阻力明显小于直翼的阻力。在其他位置，两种水翼所受的阻力几乎相同。

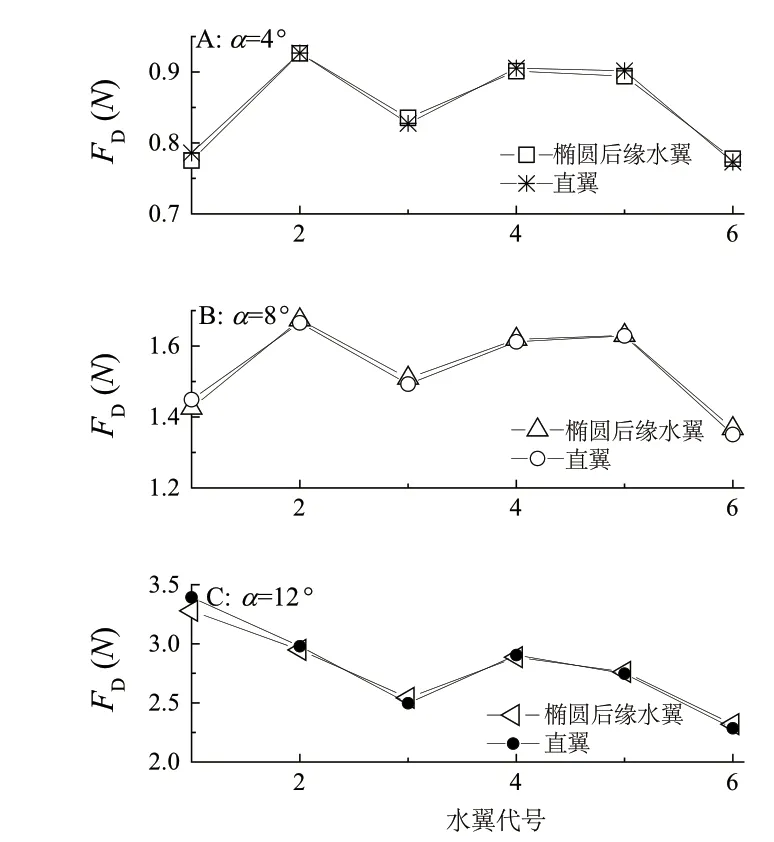
图14 各水翼在不同攻角下的阻力

3 结 论

水翼是波浪滑翔机的关键动力部件，平面形状对水翼的动力特性有很大影响。根据工作条件，研究了翼型、展弦比等因素对水翼动力特性的影响；在此基础上研究提出了基于椭圆形后缘外形的水翼平面外形的技术方案，对比分析了目前常用的平直水翼与椭圆后缘水翼的动力特性，研究结论如下。

（1）波浪滑翔机水翼的展弦比的范围约为3.85～5.22；在波浪滑翔机低雷诺数运动条件下，展弦比在此小范围内的变化对水翼升力系数的影响相对较小；波浪滑翔机水翼设计中常用翼型为NACA0012翼型和平板翼，当攻角较小时两者的升力特性无明显差异，当攻角较大时基于NACA0012翼型的水翼的性能优于平板翼。

（2）平面形状对水翼的动力特性有一定的影响。对于相同面积的水翼，当攻角较小时，椭圆尾缘水翼的升力系数和阻力几乎与平直水翼相同。当攻角较大时，椭圆尾缘水翼的升力系数优于平直水翼，而阻力小于平直水翼。

（3）水翼阵列可以有效地改善波浪滑翔机水翼的升力特性，在大攻角情况下，升力特性的改善效果更加明显。对于阵列化水翼，具有椭圆后缘的水翼的动力特性优于平直水翼，尤其在运动攻角较大时，前者的升力系数明显高于后者。

除后缘外形外，波浪滑翔机水翼的前缘外形同样对水翼的动力特性有一定的影响，且对防止水下悬浮物的缠绕起到较好的作用，对水翼外形及布局形式的进一步优化将会成为改善波浪滑翔机机动性能的研究重点之一。