重叠网格技术下振荡水翼的水动力特性

何广华，莫惟杰，王 威，刘朝纲

(1.哈尔滨工业大学(威海) 海洋工程学院，山东 威海 264209；2.哈尔滨工业大学 机电工程学院，哈尔滨 150001；3.山东船舶技术研究院，山东 威海 264209)

天然化石能源依然是当今世界能源消耗的主要来源；这些不可再生能源的大量消耗，在为全球经济高速发展带来动力的同时，也给人类的生活环境质量带来了极大的挑战[1]。为此，世界各国都在积极地开发和利用可再生的环保能源，其中潮流能依靠太阳和月球的引力产生动能，这种可再生的清洁能源具有周期性特点，能量密度是太阳能的30倍、风能的4倍[2]，且资源分布丰富。因海水的密度约为空气的1 000倍，发电机输出相同功率时，水轮机的半径只需风机的1/2[3]，所以在近海处潮流密集地区，尤其流速高于2 m/s时，非常适宜布置潮流能发电装置。

潮流能发电的装置按工作原理的不同主要分为水平轴水轮机、垂直轴水轮机、振荡水翼式发电装置。其中水平轴水轮机的开发和利用最为完备和成熟；垂直轴水轮机具有对于来流方向不敏感的特点，但是能量利用率偏低。振荡水翼式发电装置的能量捕获效率较高，浅海领域的应用优势明显[4]，并且加工工艺简单，应用前景较好。

1981年，Mckinney等[5]进行了利用振荡翼捕获来流能量的实验，并就实验值和理论解进行了对比，并对理论公式进行了修正。Zhu[6]设计了被动式单翼的获能机构，依靠弹簧提供的回复力实现水翼在线性剪切流作用下的升沉、俯仰运动，发现在小剪切率下水翼仍能保持周期性振荡。王俊芳[7]研究了二维水翼在不同攻角、雷诺数、摆动频率和幅值条件下的水动力性能。

专家学者针对双水翼获能效率的研究取得了一定的成果。王勇等[8]对NACA0015型双水翼的获能效率进行了研究，指出双水翼耦合振荡捕获潮流能装置在一定条件下获能效率可达40%. 刘海宾等[9]研究了二维双水翼的俯仰振幅存在90°的相位关系时的获能效率，并指出了NACA0018翼型的获能效率相对较好。黄凤跃[10]基于Theodoersen理论分析了大攻角NACA0018振荡薄翼非定常绕流的水动力特性。马鹏磊等[11]研究了垂直轴振荡水翼的水动力特性，指出水翼在不同的俯仰振幅下均存在“最优频率”使水翼的能量提取效果达到最佳。谢玉东等[12]研究了振荡水翼在非均匀流条件下的能量提取性能，指出水翼的攻角在30°附近时，流速在垂直方向的非均匀分布会提高水翼的时均功率系数。

近些年，研究改进翼型水翼的水动力的特性也逐渐受到关注。马鹏磊等[13]研究了改进翼型做俯仰运动时的水动力特性，通过改变水翼振荡的运动方式使其在潮流中获取更多的能量。郭春雨等[14]分别通过试验和数值模拟比较了普通前缘水翼和波浪形前缘水翼的水动力性能，发现波浪形前缘水翼结构可有效减弱表面涡流分离对水翼的扰动，提高水翼的水动力性能。

已发表的数值研究结果多是针对前后串联式双水翼、翼间距较大的并行双水翼，而关于地翼效应的双翼研究并不多见。为了实现小间距双水翼的模拟，本文采用重叠网格技术对振荡水翼的水动力性能进行研究，并分析翼地效应在振荡双翼接近时的影响。

1 数值模拟方法及验证

1.1 数学模型

本文所用数学模型的相关控制方程如下：

1)连续性方程。

(1)

式中：ρ为流体密度；t为时间；ui为流体介质在笛卡尔坐标轴i方向上的速度分量；xi为i轴方向的坐标，i=1,2,3。

2)动量方程。

(2)

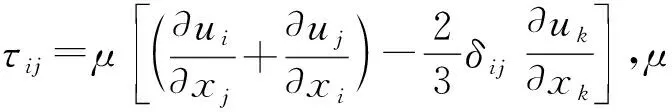
3)湍流方程。

SSTk-ω模型由Menter[15]提出，它综合了标准k-ω模型近壁区计算和标准k-ε模型远场计算的优点，适用于翼型计算：

(3)

(4)

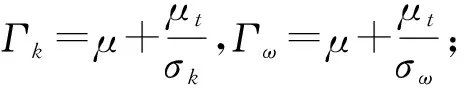
1.2 水翼的流域边界条件及获能效率

本文采用重叠网格技术处理水翼的运动问题，计算域的边界条件如图1所示，水翼的边界为壁面条件。水翼周围的网格属于组分网格，它重叠在流域背景网格内部[16]，组分网格在背景网格平面内运动。两部分网格之间通过挖洞和嵌入实现耦合[17]，即数值计算时先将背景网格中与组分网格对应的区域删除，然后通过相邻网格单元的插值实现组分网格和背景网格的数据传递。

图1 计算流域边界条件及重叠网格结构

通过自定义函数(user define function,UDF)的方式实现组分网格的运动，如图1所示，水翼的运动方程为:

h=h0cos(2πft)

(5)

θ=θ0sin(2πft)

(6)

式中：h为水翼的垂向位移，h0为升沉振幅；f为水翼的振荡频率；θ为水翼绕转轴的摆角(俯仰角)，θ0为摆角幅值。

水翼的阻力系数CD、升力系数CL、力矩系数CM分别为:

(7)

(8)

(9)

式中:FD、FL、M分别为水翼的阻力、升力、力矩；U∞为来流速度；S为水翼的弦长c与展长l的乘积，l在二维计算中取单位长度。

水翼获能的瞬时功率P为升力FL与俯仰力矩M做功之和，即

(10)

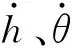
(11)

式中T为水翼的振荡周期。

水翼的瞬时功率系数CP为

(12)

(13)

振荡水翼的总功率P0定义为

(14)

式中H为水翼的扫掠高度，它与展长l的乘积为水翼的扫掠面积。

振荡水翼在潮流中的获能效率η为

(15)

1.3 模型验证

运用上述数学模型对振荡水翼做数值模拟分析，按照Kinsey等[18]给出的运动参数，选取NACA0015翼型，取弦长c=0.25 m，折算频率[19]f*=fc/U∞=0.14，θ0=60°，h0=0.25 m，水翼转轴位置L1取为c/3弦长位置处，来流速度U∞=2 m/s，分析流域边界尺度、网格密度对计算收敛性的影响，使得水动力计算结果对以上两者不再敏感。

1.3.1 网格无关性验证

本文使用了重叠网格技术，网格密度调整时应当按照一定比例，同时协调组分网格和背景网格的密度，改变翼型表面节点个数的同时，背景网格的密度以及其各个加密区的网格密度也都要一起做相应调整。本文根据相同的比例设置不同的网格数量(见表1)，网格A和B的获能效率分别和较密的网格C比较，网格B的误差为1%以内，选择网格B的划分密度作为本文的网格密度。

表1 网格密度无关性验证

采用重叠网格技术中，水翼所在的组分流域网格需在背景流域网格内周期运动，在过小的计算域中，湍流难以得到充分发展，容易出现边壁反射、出口回流等影响计算精度的问题，因此对流域的尺寸做无关性验证。选取网格B中的密度标准，对不同流域尺度验证结果见表2。可以发现当流域尺度大于70c×70c后，水翼的效率趋于稳定，本文选取的流域尺度为70c×70c.

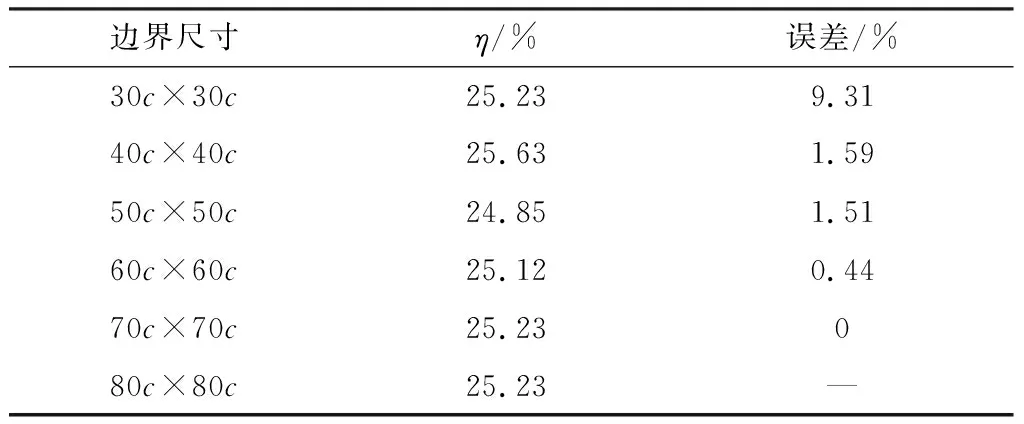
表2 计算域收敛性验证数据表

1.3.2 模型有效性验证

选取流域边界尺寸为：70c×70c，网格数目为8.2万，θ0=60°和θ0=75°，水翼的水动力计算结果与文献中的翼型研究结果对比见表3、4。从表3、4可以看出，计算结果和文献[18]的结果相差5%以内，充分验证了本文数值计算方法的有效性。

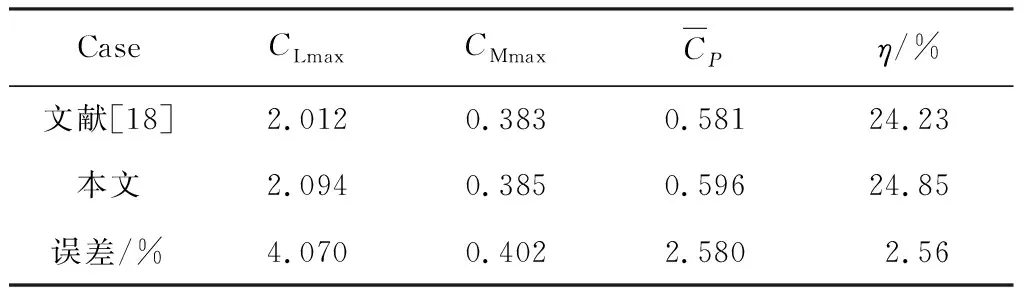
表3 振荡水翼的计算结果验证(θ0=60°)

表4 振荡水翼的计算结果验证(θ0=75°)

2 振荡水翼数值模拟结果与分析

2.1 水翼运动及结构参数的影响

首先研究单翼在水流中振荡运动时的水动力特性，本文针对NACA0016型水翼进行分析，来流速度U∞=2 m/s，弦长c=0.25 m。

2.1.1 折算频率

图2给出了振荡水翼在不同折算频率条件下的获能效率变化曲线，水翼的摆角幅值θ0=60°，升沉振幅h0=1c。

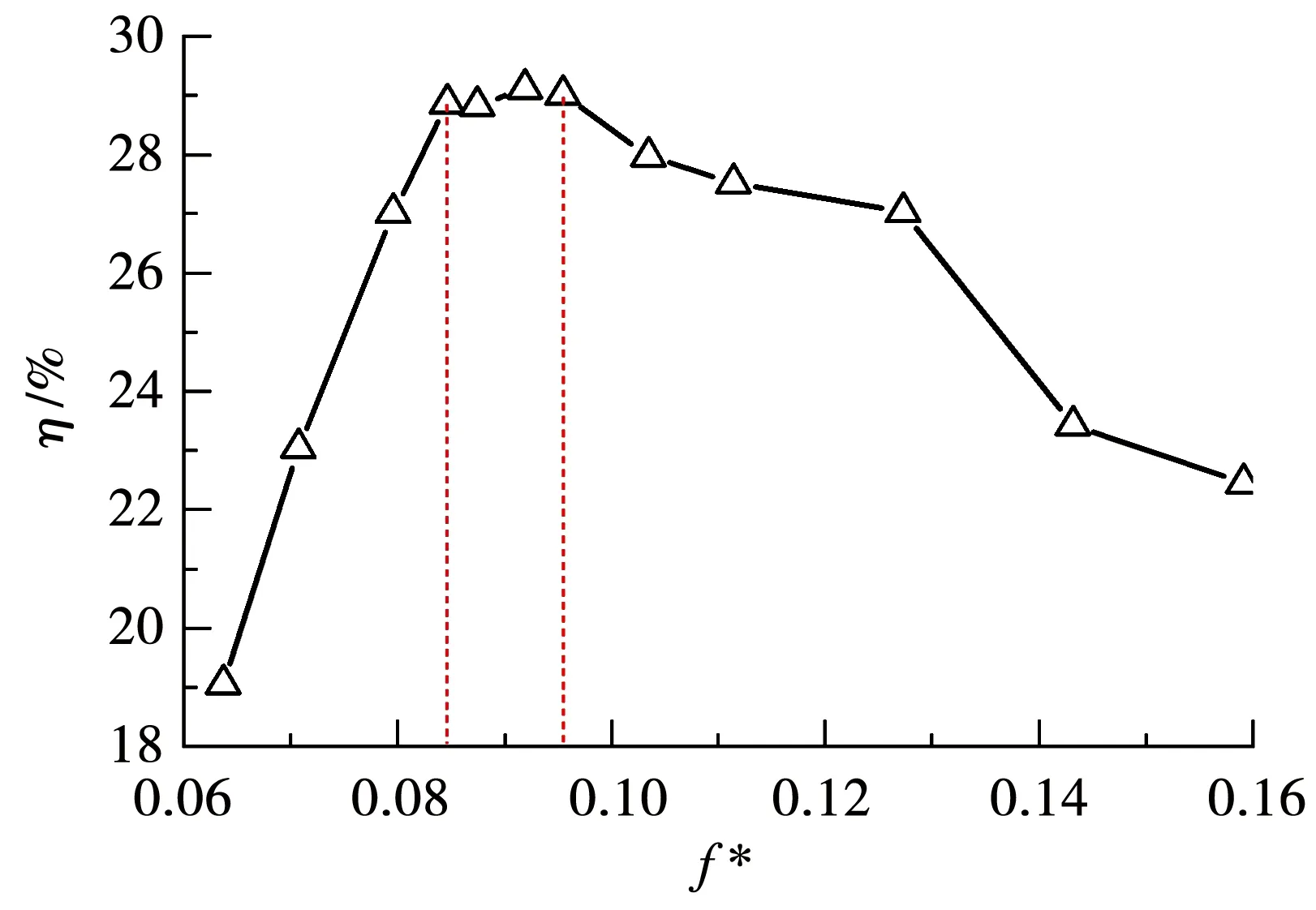
图2 折算频率对获能效率的影响

从图2可以看出：水翼获能效率η随着折算频率f*的增加呈现先增大后减小的趋势。f*在0.085～0.095之间的获能效率较高，最高可达29%左右；f*<0.085时，因水翼折算频率的增加，水翼的垂向运动速度和摆动角速度逐渐增大，水翼的获能效率逐步增加；f*>0.095以后，水翼的获能效率下降。为分析获能效率下降的原因，f*分别取0.095和0.143时，水翼的3自由度水动力时历曲线如图3所示。

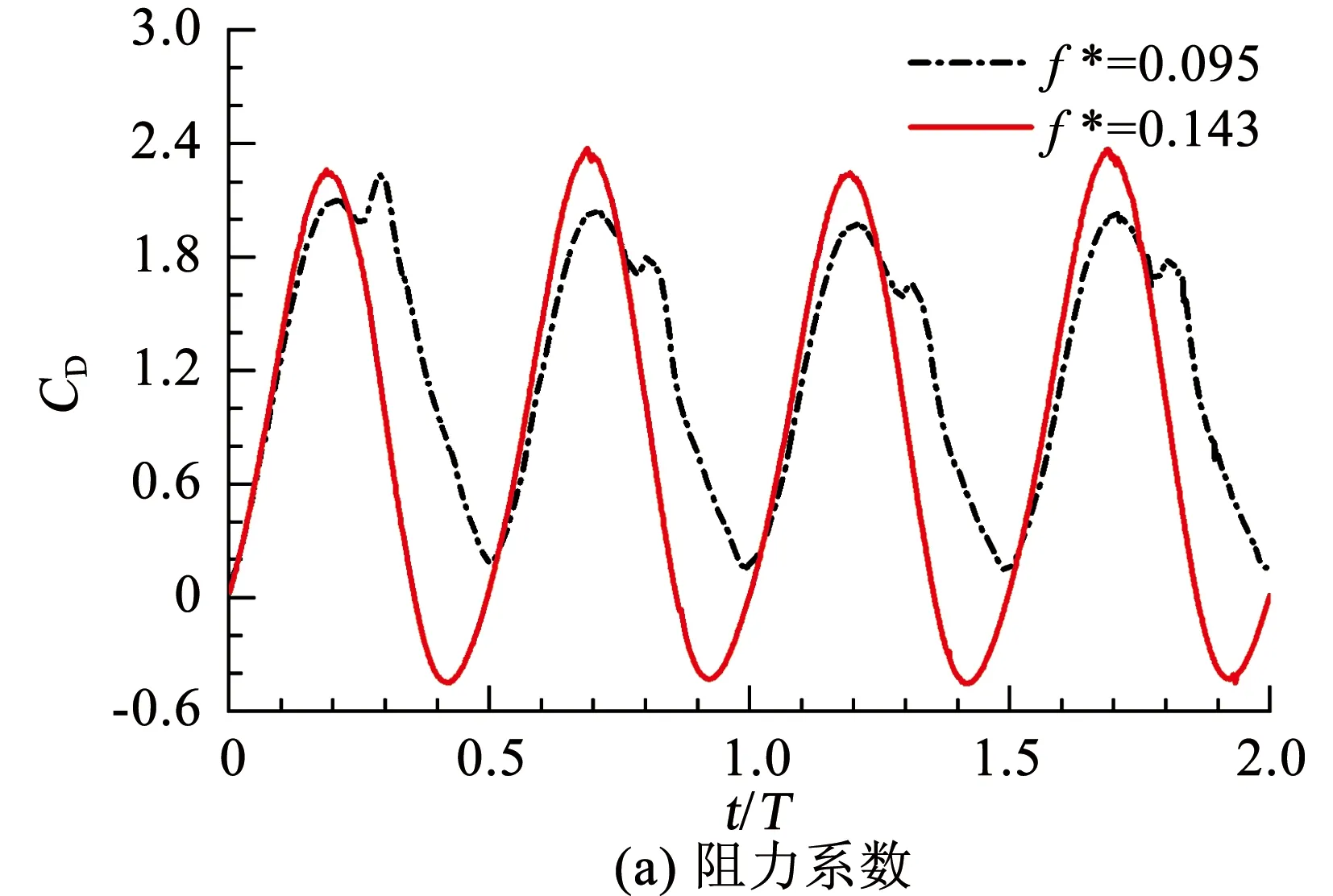
图3 振荡水翼两个周期内的受力时历曲线

从图3可以看出，随着摆动频率的增大，水翼的阻力幅值略有提高，但文中水翼并无水平方向的运动，所以阻力对获能效率的影响较小；升力幅值对应的时间点向前移动，但幅值变化不大，对获能效率的影响不大；而力矩系数因水翼振荡频率的减小发生了较大变化，频率较小的时候，力矩系数的峰值处会出现反方向的“塌陷”，这种力矩变化造成了水翼获能效率的差异。因力矩的做功和角速度有关，文中定义量纲一的角速度Θ为

(16)

力矩和角速度为同一方向时，水翼是捕获能量的，取力矩和角速度的时历曲线如图4所示。图4中以量纲一的时间t/T=1.5左右的范围为例，折算频率为0.095条件下，力矩系数的峰值处的“塌陷”使得力矩和水翼的转动同向，力矩对水翼做正功，水翼处于获能状态；而折算频率为0.143条件下，力矩系数和水翼的转动反向，力矩对水翼做负功，水翼的获能效率下降。

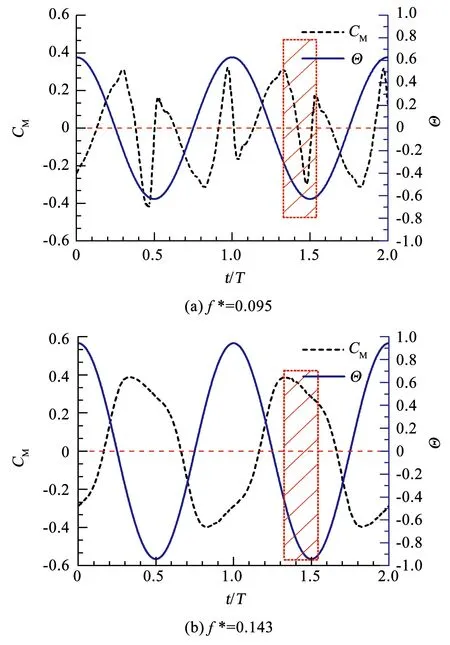
图4 振荡水翼的力矩系数和量纲一的角速度的时历曲线

分析小频率条件下水翼力矩系数峰值“塌陷”的原因，流场漩涡结构的变化是影响水动力的直接因素[13]，取t/T=1.35～1.50的范围为例，水翼的漩涡结构如图5所示。该时刻水翼逐渐摆动到最下方的水平位置，因迎/背流面的压差作用，水翼前缘表面因流动分离而产生漩涡，漩涡附近的压力较低，漩涡沿水翼表面向下游运动时，会影响水翼所受的力矩方向，从而出现了图3(c)中的力矩系数曲线的“塌陷”变化。

图5 振荡水翼运动过程中的涡脱落

2.1.2 摆角幅值

由式(15)知，水翼的扫掠高度H对水翼的获能效率η有重要影响。从图1可知水翼转轴距离前缘长度为L1，距离后缘长度为L2，那么前缘和后缘的扫掠高度H1和H2分别为:

H1=2(h-L1sinθ0)

(17)

H2=2(h+L2sinθ0)

(18)

那么振荡水翼的实际扫掠高度H为

H=max(H1,H2)

(19)

可见振荡水翼的摆角幅值θ0对获能效率η存在影响。设定水翼的转轴位置L1=c/3，研究不同的摆角幅值对水翼获能效率的影响，如图6所示。

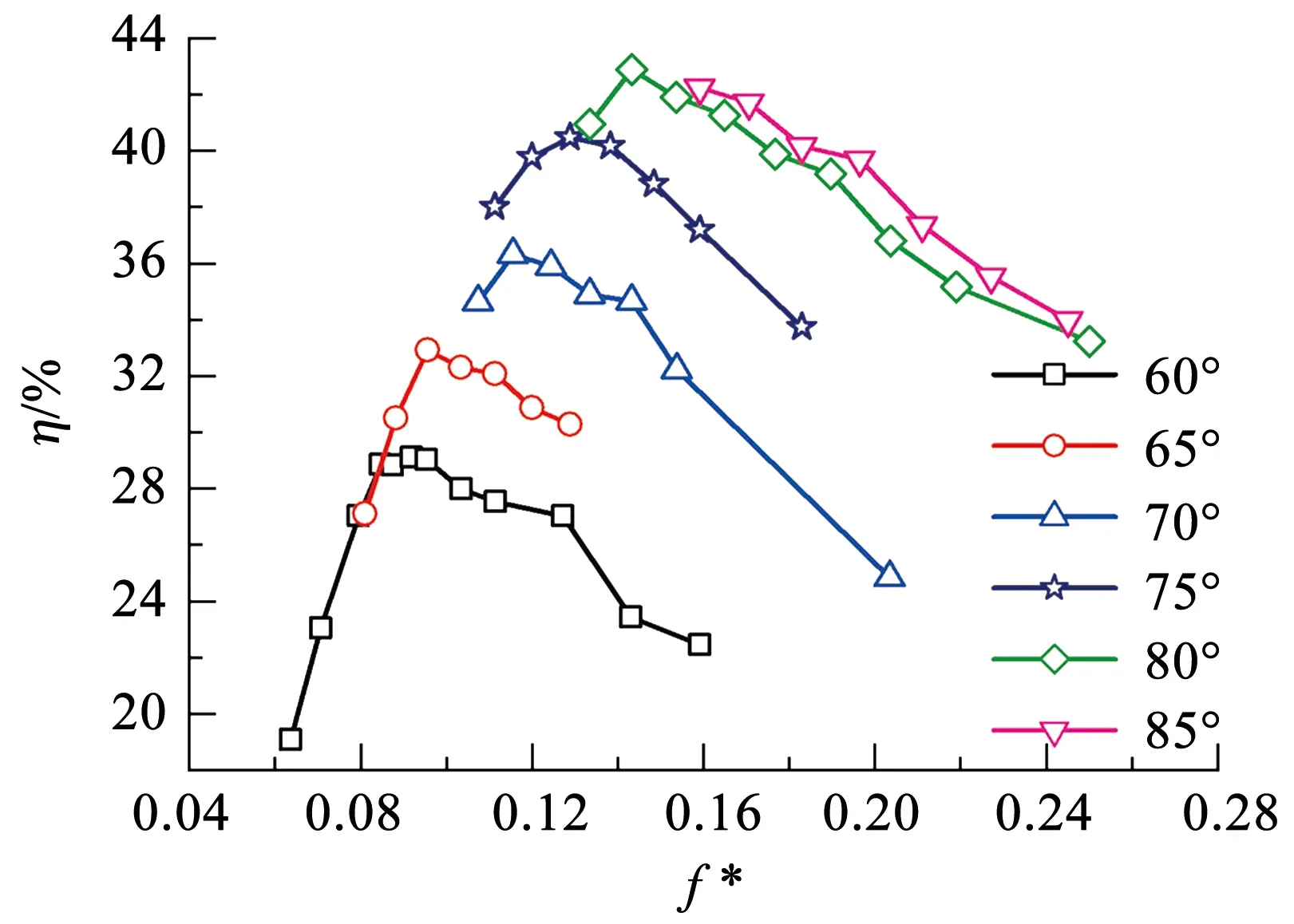
图6 摆角幅值对水翼获能效率的影响

从图6可以看出：随着摆角幅值的增大，总体上水翼获能效率会得到提高；因为小幅度地增加摆角幅值会提高水翼的有效攻角，会提高获能效率。但是过大的摆角幅值会使振荡水翼的有效攻角接近失速角，降低振荡翼的水动力性能，并且扩大了水翼对来流的扫掠高度H，由式(15)知水翼的获能效率η也会减小。

从图6可以发现：每个摆角幅值曲线中最大获能效率所对应的折算频率f*也会随摆角幅值的增大而增大；摆角幅值在80°附近时，振荡水翼最大获能效率η达到42.89%，说明振荡水翼的摆角幅值处于75°～80°时，水翼的获能性能较好，这与文献[9]的结论一致。虽然较大摆角幅值的水翼在高频条件下的获能效率要比较小摆角幅值的水翼在低频条件下的获能效率高，但是较高的摆动频率对潮流的流动环境及振荡水翼发电装置的稳定性也提出了较高的要求，所以追求提升振荡水翼获能效率的时候，要兼顾最优获能频率和摆角幅值的综合影响。

2.1.3 升沉振幅

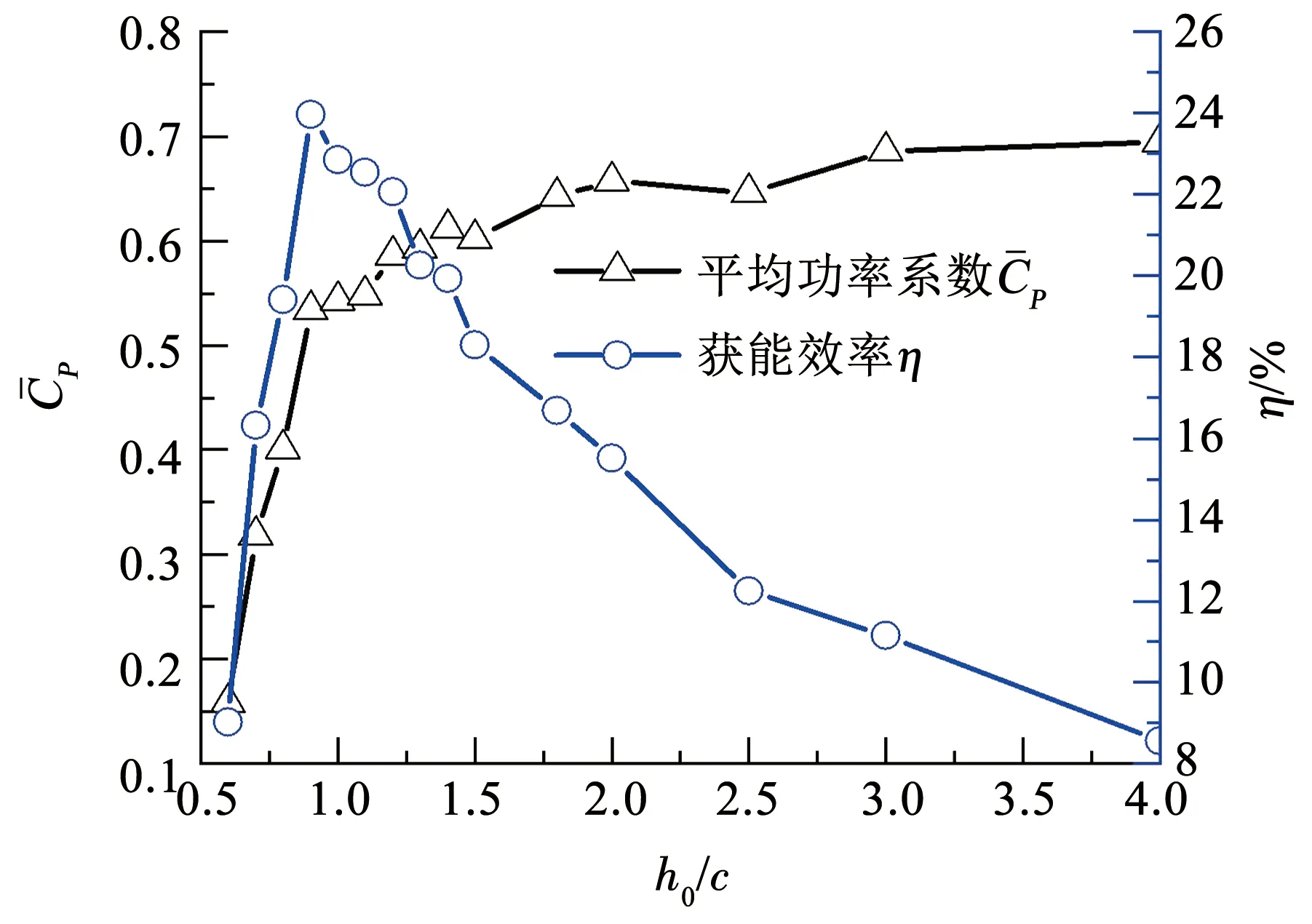
图7 升沉振幅对水翼获能效率的影响

2.1.4 转轴位置

为综合研究振荡水翼的水动力性能，进一步分析了水翼的转轴位置对获能效率的影响，转轴距离水翼前缘的距离为L1，不同转轴位置水翼的获能效率变化如图8所示。

从图8可以看出：随着转轴位置L1的逐渐增大，水翼的获能效率η曲线呈现先增大后减小的趋势；当水翼的转轴位于距离前缘的1/3弦长附近时，水翼的获能效率最佳。后文的研究中取1/3弦长的位置作为振荡水翼的转轴。

图8 转轴位置对水翼获能效率的影响

2.2 翼地效应

翼地效应是指运动物体贴近地面飞行时，地面对物体产生的空气动力干扰，影响到空气对飞行器的绕流特性，使飞行器上下压力差增大、升力增加，获得比空中飞行更高升阻比的流体力学效应。对于平行对称布置的双翼，随着上下两个水翼的不断接近，双翼之间会形成类似翼地效应的高压，使双翼分别获得更大的升力，提高双翼的能量捕获性能。

2.2.1 双翼间距

根据上文的研究结果，选取水翼的摆角幅值θ0=80°，折算频率f*=0.16，转轴位置L1=c/3，双翼之间的最小距离设为1～6倍弦长时的能量捕获效率见表5。

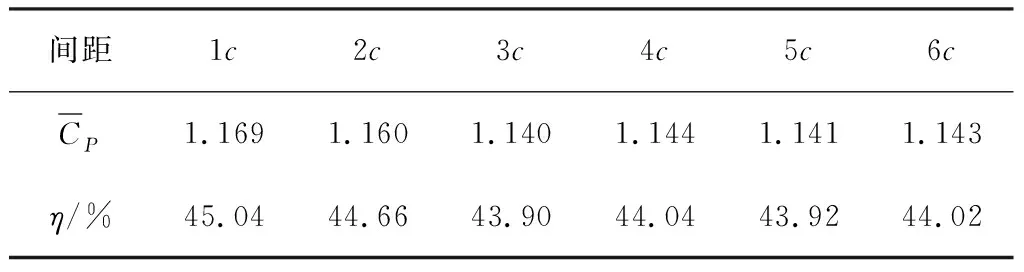
表5 振荡水翼间距对能量捕获效率的影响

从表5可以看出对称双翼的上下间距扩大过程中，水翼的能量捕获效率逐渐减小并趋于平稳，但是变化范围并不大；说明水翼间距较远时双翼彼此的影响会逐渐减小，并与各翼单独运动的情况趋于相同，所以研究对称双翼间的翼地效应对获能效率影响主要侧重于双翼间距小于1倍弦长的情况。

2.2.2 翼地效应分析

对称双翼之间的运动规律是对称的，它们的相位差为π. 为避免双翼发生碰撞，选取双翼的摆角幅值θ0=60°；根据图6的结果，选择折算频率f*=0.08，振荡水翼的工况见表6。

表6 翼地效应的工况

在水翼摆动数个周期后回到平衡位置时，提取表6中流场的压力分布见表7。比较发现，相较于单振荡水翼的工况1，双振荡水翼的工况2系统中，两水翼的距离接近时，翼面之间形成了高压区。这是因为随着双翼距离的不断靠近，两个水翼相互充当“地面”，依靠翼地效应在双水翼之间形成了高压区，并使水翼两侧压差增大，提高了水翼的升力，使水翼的能量捕获效率η从工况1中单翼情况的24.86%达到工况2中双翼情况的25.27%，而工况3的能量捕获效率达到25.41%。

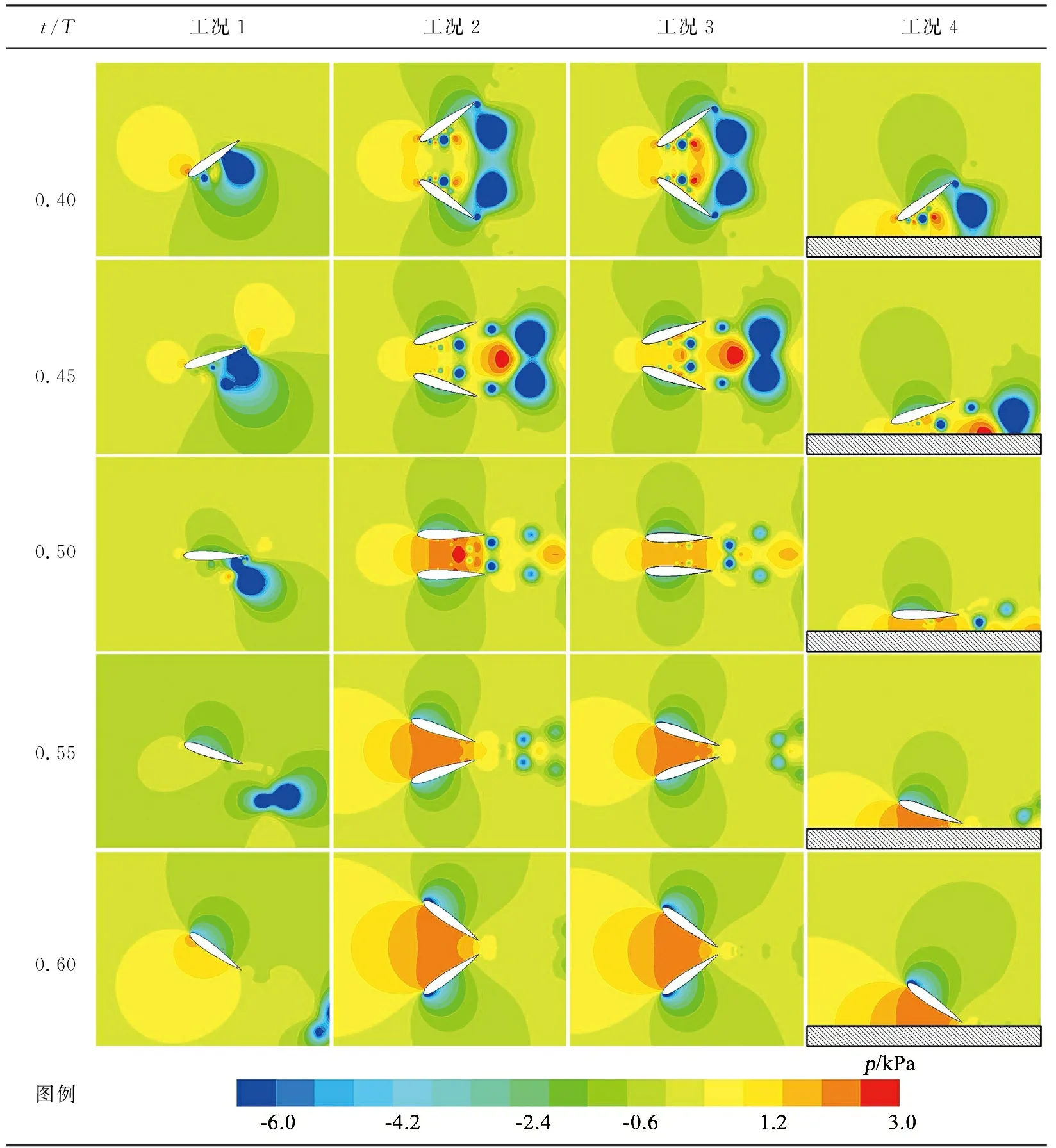
表7 翼地效应下压力云图

工况3中流场的压力分布与工况2相似，工况4主要起到对比分析的作用，给出了单个振荡水翼与固定平板组成的能量捕获系统的流场压力分布情况。从表7工况4中可以看出当水翼与平板的距离较近时，两者之间的确形成了高压区域，水翼会获得更大的升力，此时的获能效率为27.51%。而水翼与平板或者双水翼的距离较大时，流场的压力分布状况与单水翼相似。通过以上分析可知，双翼彼此之间在系统中互相充当了“地面”，形成了翼地效应。

进一步分析水翼的升阻比性能，升阻比K定义为水翼升力系数和阻力系数的比值如下:

K=CL/CD

(20)

在水翼逐渐远离运动轨迹平衡位置(或水翼从平板附近远离)的时候，分析水翼的升阻比变化特性。因形成翼地效应的时间较短，所以只分析前T/64的时间段即可，各工况水翼的升阻比K的变化如图9所示。可以发现工况1中单水翼的升阻比相对较小，其最大值仅为38.4；工况2中双水翼的升阻比最大值为51.8；工况3中双水翼的升阻比最大值为87.4；工况4单水翼和平板系统中，升阻比高达101.9；说明双翼的距离越小，翼地效应对振荡水翼升阻比的影响越明显。

图9 翼地效应时各工况水翼的升阻比曲线图

3 结 论

1)振荡水翼的能量捕获效率η随着折算频率f*的升高而先增加后减少，折算频率处于0.085～0.095区间时，水翼的能量捕获效率较高，而涡脱落对获能效率存在重要影响。

2)振荡水翼的获能效率η总体上随着摆角幅值θ0的增加而增加，但受有效攻角αe和扫掠高度H的影响，获能效率的提升要兼顾最优获能频率和摆角幅值的综合影响，当折算频率处于获能最优区间时，摆角幅值在75°～80°的范围内，振荡水翼的获能性能较好。

3)振荡水翼的升沉振幅h0在1倍弦长附近，转轴距离前缘1/3弦长位置时，水翼的能量捕获效率较好。

4)双振荡水翼互相靠近时，两翼之间相互作用形成了翼地效应的现象，水翼之间的流场形成高压区域，水翼的升阻比大幅度提高，提升了水翼的能量捕获性能。