DWS19微型捷联惯性波浪传感器

周峰华， 张荣望，谢 强

( 1.中国科学院南海海洋研究所，广东 广州 510301；2.中国科学院深海科学与工程研究所，海南 三亚 572000 ）

在海洋波浪观测领域，惯性波浪观测设备因其不受时空范围影响、观测周期范围广等优势，自问世以来一直是海洋波浪观测的主要手段。随着越来越多对波浪快速、机动、隐蔽观测的需求，波浪浮标的体积也在逐步向小型化、低功耗、低成本发展[1-4]。0.6 m以下的小型化波浪浮标的随波性更好，在水中的姿态变化相对于大型浮标来说横滚、摇摆等幅度更大，必须解决波浪核心惯性感知部件的水平稳定问题[5]。传统的波浪浮标中水平保持主要采用平台惯导型（机械/机电），其对装配环境要求高、成本更高，往往一个机械/电稳定平台的成本就高达整个惯导系统成本的50%以上，且体积和重量均较大，不利于在小型波浪漂流浮标上使用[5]。本文介绍中国科学院南海海洋研究所自主研制的DWS19微型捷联惯性波浪传感器，及其捷联姿态补偿、频域数值积分、波浪谱在线计算等关键技术实现。捷联型“数字稳定平台”使波浪传感器彻底摆脱对外部机械/电稳定平台的依赖，可独立安装并实现在动态环境中波浪的精准测量。DWS19型波浪传感器体积小、功耗低、成本低，已完成多次海上观测实验、标准转台比测，测量精度较高，满足科研、工程、业务部门波浪观测需求。

1 DWS19传感器关键技术

浮标在波浪的作用下随波起伏、摇摆，能否在动态波浪环境下保持惯性感知部件的水平稳定，直接影响波高的测量精度[6]。姿态稳定保持有平台式和捷联式两种方法，随着未来对波浪传感器小型化、快速机动布放的要求，捷联式是主要的发展方向[7-8]。图1(a)为平台式稳定机构，图1(b)为搭载平台式稳定机构的波浪浮标借助于万向节式的机械垂摆结构使惯性感知部件始终处于水平稳定状态，进而对垂直方向的加速度进行积分获取波浪、周期等特征信息。图2为DWS19波浪传感器，内嵌捷联姿态解算、补偿算法，可实时测量波浪随波晃动的三轴姿态（横滚、俯仰、航向），对载体坐标系的三轴加速度进行3次坐标旋转变换到自然坐标系，获取垂直方向的加速度。通过数学方法实现机械/电稳定平台功能，因此传感器的体积、功耗、成本都会大幅降低，方便携带和安装，满足快速、机动、隐蔽布放场合的需求。

图1 平台式稳定机构

图2 DWS19微型捷联惯性波浪传感器

目前测波技术中常用的有硬件积分、时域数值积分和频域数值积分[9]。硬件积分通过搭载硬件积分电路，实现将加速度模拟信号到位移模拟信号的2次积分，因硬件在设计之初就已定型，因此积分电路的滤波性能是固定，对于周期随机变化较强的波浪来说，硬件积分不具备滤波自适应性。时域数值积分会因惯性部件加速度信号的微小直流偏差造成2次积分后位移结果的趋势漂移，需要经验性滤波去除趋势项，方可提取真实的位移信号。近年来，在波浪数值积分中越来越多采用频域积分方法，频域积分可以有效避免由于低频直流误差信号带来的趋势漂移问题，使积分结果更准确。

DWS19微型捷联惯性波浪传感器的研制过程中，重点解决捷联姿态补偿、频域数值积分和波浪谱在线计算3个关键技术。

1.1 DWS19总体介绍

图3为DWS19型波浪传感器硬件组成框图，包括惯性单元、高性能嵌入式处理器、通讯接口、电源系统、SD卡存储等部分。惯性单元是DWS19的核心感知部件，采用美国ADI公司生产的战术级9轴惯导模块ADI16488, 内嵌温度补偿，各轴均有自己的动态补偿算法，满足工业级惯性测量需求。为满足波浪姿态解算、旋转矩阵、FFT等对实时计算要求较高的需求，选用ARMCortex-M4高性能嵌入式处理芯片，该芯片对姿态实时解算最高可达100 Hz，完成一组4 096点FFT的时间不大于20 ms，满足波浪实时计算的需求。DWS19内嵌捷联惯性波浪测量算法流程为，传感器上电后进行自身的软硬件初始化，5 s后开始以4 Hz频率采样9轴数据，并同步进行融合滤波姿态计算、加速度坐标系补偿，当采样点数达到4 096或2 048后进入波浪计算程序，先后进行频域数值积分、时域跨零波浪特征统计、波浪谱特征计算等，每组采样的载体系加速度、三轴倾角、自然系加速度等原始数据均会记录在SD卡中，波浪计算结果通过串口向上位机输出并同步存储在SD卡文件中。每组波浪计算结果的输出格式为：$wave,yyyymmddhhmmss,,,, ,,,,,,,,,,,,,< cr>< lf>，其中各变量意义：

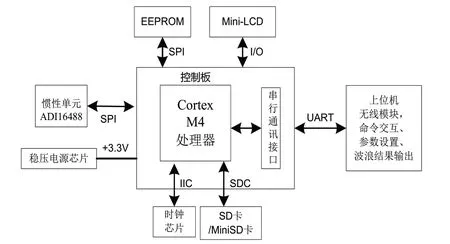
图3 DWS19硬件系统框图

hmax_t：最大波高-跨零法；tmax_t：最大波周期-跨零法；h3_t：1/3大波高-跨零法；t3_t：1/3大波周期-跨零法；h10_t：1/10大波高-跨零法；t10_t：1/10大波周期-跨零法；ha_t：平均波高-跨零法ta_t：平均波周期-跨零法；CroPoints: 跨零点数；Dm: 主波向；tmax_s：最大波周期-谱方法；h3_s：1/3大波高-谱方法；t3_s：1/3大波周期-谱方法；h10_s：1/10大波高-谱方法；t10_s：1/10大波周期-谱方法；ha_s：平均波高-谱方法；ta_s：平均波周期-谱方法。

1.2 捷联姿态解算和姿态校正

波浪随波晃动的姿态角实时估计是“波浪数字稳定平台”的关键所在，利用MEMS陀螺仪和加速度通过数据融合方法获取姿态角的方法已被广泛应用在姿态测量、姿态控制、姿态补偿等场合[10-11]。加速度传感器具有较好的静态响应特性，静止状态下可以根据重力加速度分解准确得到姿态角。陀螺仪具有较好的动态响应特性，但是在长期的使用中会因温漂存在，产生累计误差，故需要用加速度数据补偿陀螺仪的数据，进行角度修正，因此需合理融合这两种传感器的数据，得到最优估计的姿态数据[12]。

本文采用互补融合滤波算法，通过设计合理的互补滤波器系数，可实现在波浪动态环境下三轴姿态角测量精度不大于0.1°。进一步，根据公式(1)由三轴姿态角计算载体系到自然地理坐标系的坐标旋转矩阵（）。

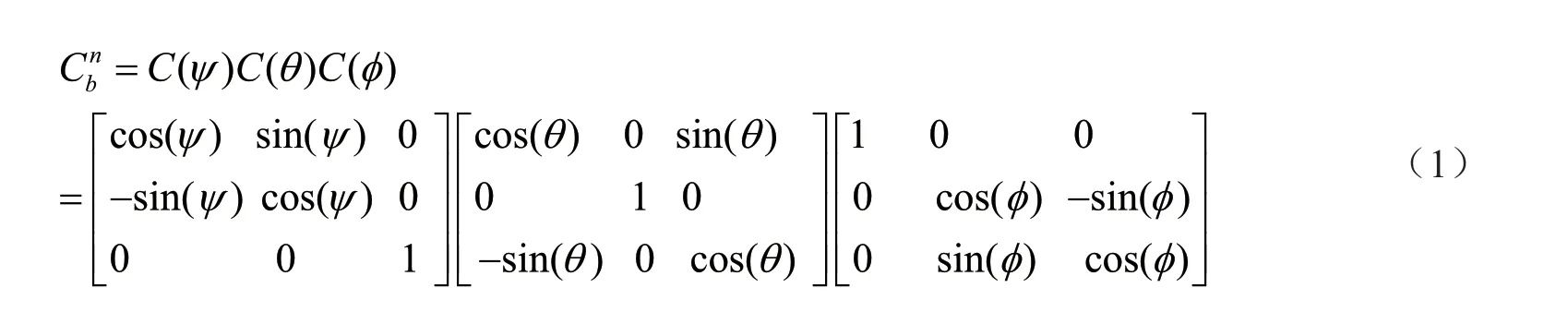
式中：ψ，φ，θ分别为上一步得到的最优估计横滚、俯仰和航向角。

图4 捷联姿态解算流程

图5 为一组从直径为0.9 m波浪浮标上使用DWS19-2漂流型波浪传感器采集的长度2 048点载体系Z轴加速度信号和姿态校正后水平系Z轴加速度和积分后的位移信号对比图。从图中可以看出，进行捷联姿态校正后，加速度和积分后的位移均有明显区别，其中位移误差可达10%，可见在小型测波平台上姿态校正是必要的。

图5 姿态校正前后加速度和位移对比

1.3 加速度-位移频域积分

频域积分是先对加速度信号进行傅里叶变换（FFT），将时域加速度信号变换到频域，根据傅里叶变换的积分性质，频域内的2次积分就变成了傅里叶分量系数的积分运算，将积分结果再进行傅里叶反变换（IFFT）到时域位移信号。研究表明，相对于时域数值积分来说，频域积分可以有效抑制低频直流误差信号在两次积分过程中的误差累计放大效应，积分得到的位移结果更加准确可靠[13]。随着高性能ARM、DSP芯片计算性能的大幅提升，在嵌入式芯片中实现FFT、IFFT计算已可行[14]。DWS19-1/2两型波浪传感器在加速度-位移的积分方法上均选择采用频域数值积分方法，计算流程为：按照公式（2）对一组水平系Z轴加速度an进行归一离散FFT，分别得到FFT后的实部和虚部。

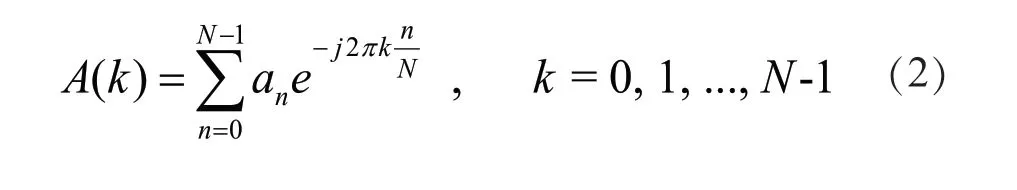
按照傅里叶积分变换性质，根据公式（3），完成加速度到位移的2次积分计算，并对位移信号进行1.5～ 20 s的滤波，最后进行IFFT得到时域位移信号。

图6为一组实测Z轴加速度数据分别采用频域和时域两种方法积分后得到的位移序列对比。从图中可以看到，时域积分的位移结果出现了明显的趋势漂移，后期需要采用经验性信号滤波处理方法提取真实的位移信号[15]，而频域积分并不存在结果的趋势漂移，得到为真实的波浪随波上下运动的位移。

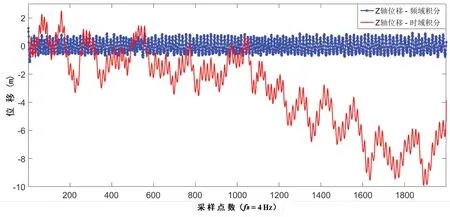
图6 加速度-位移频域积分对比

1.4 谱反演波浪特征参数

经过1.3频域积分，已经得到位移数据。DWS19型波浪传感器内嵌程序包含时域跨零和波浪谱特征反演两种波浪参数提取方法。

对于一组波浪位移信号，在时域可通过跨零方法进行波浪特征统计。首先找出位移平均值作为基准零线，浮标向下运动位置与零线的第一次交点为跨零起点，再寻找第二次交点作为跨零终点，两个下跨零点之间的时间差为观测到的一个波周期，两个跨零点之间的垂直位移差为观测到的波高。将一组时间内观测到的所有波高和波周期进行从大到小排序，进一步统计得到最大、十分之一、三分之一、平均波高和波周期。

另外，可由波浪内部结构的功率谱反演得到波浪要素的特征值[16-17]。DWS19采用周期图法计算功率谱，公式如下。

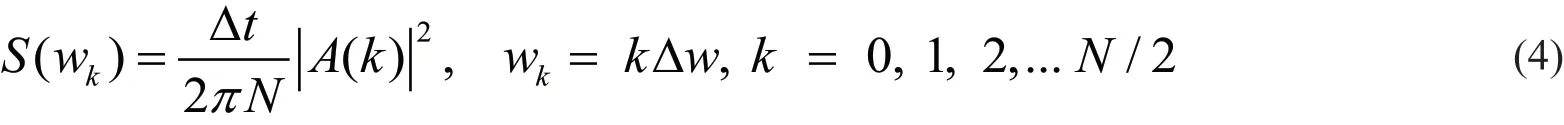
式中：A(k)是位移时间序列S(n)进行离散傅里叶变换得到，可用FFT函数计算。以上公式估计出来的谱值是粗糙的，所以S()w为海洋功率谱的粗谱，画出来的谱线也是参差不齐的。为有利于后续的分析和计算，需要进一步对功率谱进行平滑处理，按照如下公式(5)进行平滑。

接着计算波浪的各阶谱矩，其中波浪的零阶矩m0、二阶矩m2的计算公式(6)、(7)如下。

进而可以从能量的角度反演出传感器随波运动的波浪特征参数，包括平均波高ha_s，周期ta_s，有效波高h3_s，三分之一大波周期t3_s，十分之一大波高h10_s，十分之一大波周期t10_s，其中平均波高和周期的计算公式(8)、(9)如下所示。

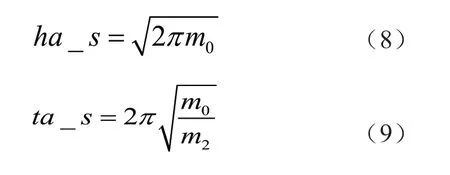
图7为一组浮标实测波浪高度数据，观测时间为2020年10月20日—21日，分别采用跨零统计和谱反演两种方法得到，从图中可以看出两种方法得到的平均波高和有效波高非常吻合，有效波高和平均波高的平均偏差分别为0.05 m和0.02 m。因所搭载的浮标体并非完全随波，所以其中谱分析得到的会略微偏大一些。如果搭载在小尺寸、随波性能好的浮标体上，两者的计算结果会更加接近。

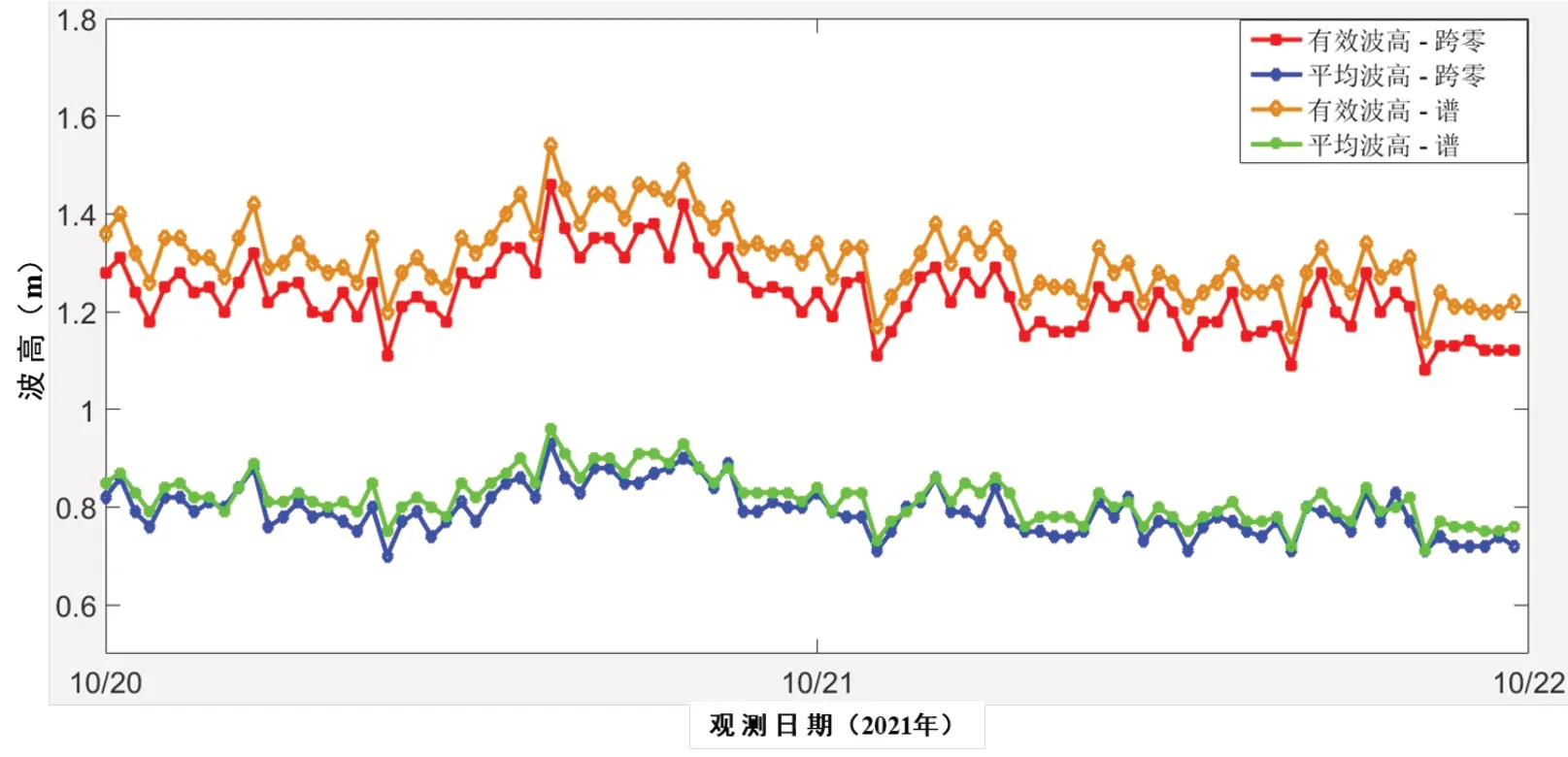
图7 跨零法和谱反演方法得到波高对比

2 实验分析

2.1 标准转台测试

DWS19-2型波浪传感器在国家海洋标准计量中心波浪校准试验室进行了1 m、3 m和6 m，3个标准高度的波浪模拟测试(图8)。测试流程为：每组标准波高上，随机制定4个标准周期首先进行1次功能性测试，然后在这4个标准周期中随机挑选1个标准周期进行5组重复性测试。因标准转台没有大小不同的高度、周期变化，且不是真实的海上波浪运动。因此选取传感器跨零法输出的平均波高、波周期与标准高度、周期进行比较。

图8 标准转台测试

在1 m标准高度上，分别进行了8.3 s、6.4 s、4.7 s和3.7 s，4个标准周期的功能性测试，并随机选择了6.4 s进行重复性测试，1 m标准高度的测试结果如表1和表2所示。

表1 1 m标准高度上4个标准周期的功能性测试

表2 1 m标准高度上6.4s标准周期5组重复性测试

在3 m标准高度上，分别进行了9.5 s、7.6 s、6.2 s和4.5 s，4个标准周期的功能性测试，并随机选择了7.6 s进行重复性测试，测试结果如表3和表4所示。

表3 3 m标准高度上4个标准周期的功能性测试

表4 3 m标准高度上7.6 s标准周期5组重复性测试

在6 m标准高度上，分别进行了9.6 s、8.5 s、7.3 s和6.4 s，4个标准周期的功能性测试，并随机选择了6.4 s进行重复性测试，测试结果如表5和表6所示。

表5 6 m标准高度上4个标准周期的功能性测试

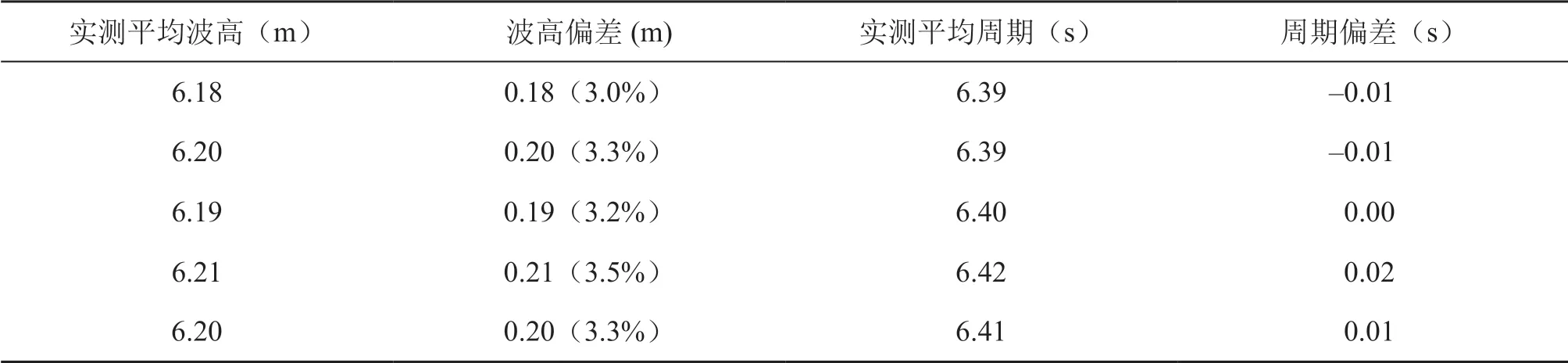
表6 3 m标准高度上6.4s标准周期5组重复性测试

总体来看，DWS19微型捷联惯性波浪传感器在1 m标准高度上，波高误差可以控制在3%以内。在3 m和6 m标准高度上，波高误差可以控制在5%以内。而周期测量精度更高，基本可以控制在±0.05 s以内。按照波浪高度观测精度等级来划分：优秀（≤5%）,良好（%5<误差≤10%），较差（>10%）, DWS19在3个标准高度上的测试均达到优秀指标等级。

2.2 浮标波浪观测

2020年9月，中国科学院“实验3”号科考船执行东印度洋科学考察航次，船上搭载1套北斗海-气耦合观测浮标，投放在4 000 m水深的印度洋赤道海区（79°E，2°N），浮标直径3 m（图9）。浮标上搭载DWS19-1型波浪传感器测量投放点的波高、周期和波向，波浪观测间隔为30 min。截至目前，浮标系统正常运行，已获取2个多月的印度洋赤道区域第一手观测数据，波浪观测数据全部正常，数据获取率100%（图10）。

图9 印度洋海气耦合观测浮标布放图

图10 2020年10月25-30日印度洋浮标波浪观测时间序列

3 结 论

本文详细介绍了DWS19微型捷联惯性波浪传感器原理及其技术实现，传感器已通过国家海洋标准计量中心波浪转台测试和大量的海洋现场观测实验，其测量精度高、体积小、功耗低、成本低，为海洋波浪快速、机动、隐蔽观测提供了一种新的测量手段，研究结论如下。

（1）DWS19内嵌捷联姿态解算方法，在国际上首次实现“数字稳定平台”功能，可摆脱对机械/电式稳定机构的依赖，体积小、方便安装，可有效提高在动态波浪环境中的测量精度；（2）DWS19采用频域积分方法实现加速度-位移的积分。相对于传统时域积分来说，频域积分对低频直流信号具有很好的抑制作用，积分结果不会产生趋势漂移；（3）DWS19在国内首次实现了波浪功率谱的板级实时计算，并通过谱方法反演波高、周期参数。通过与时域跨零方法比较，证明现场谱反演的波浪特征结果是准确、可信的；（4）标准转台测试结果显示DWS19测量精度为：波高（<5%）、周期(<±0.05 s)，达到优秀测量指标等级，接近国际先进波浪传感器水平，满足工程、科研、业务运行等场合的观测指标要求。