潮差区、浪溅区混凝土中的氯离子输运模型及仿真研究

赵昆璞，刘宗民，毛继泽

（哈尔滨工程大学航天与建筑工程学院，黑龙江哈尔滨150001）

潮差区、浪溅区混凝土中的氯离子输运模型及仿真研究

赵昆璞，刘宗民，毛继泽

（哈尔滨工程大学航天与建筑工程学院，黑龙江哈尔滨150001）

潮差区、浪溅区处于干湿交替的复杂环境中，是腐蚀劣化最为严重的区域，直接影响着海工结构的耐久性和使用寿命。为了更好地描述潮差区、浪溅区的氯离子在混凝土中的侵蚀规律，本文采用Hamilton型变分原理建立氯离子的输运方程，结合细观角度，建立了一个有效的孔隙水饱和度的定量计算公式，并引入时间因素和孔隙水饱和度对非饱和状态下氯离子的扩散系数进行修正。利用有限单元法模拟氯离子在混凝土迁移过程，并与实验数据以及水下区氯离子的计算值进行对比验证。结果表明：模型计算结果和实验数据吻合较好，并且符合氯离子输运的一般规律。验证了本文提出的模型可以为潮差区和浪溅区混凝土结构的耐久性设计及服役寿命预测提供参考。

潮差区；浪溅区；氯离子扩散系数；输运模型；孔隙水饱和度

混凝土中钢筋的锈蚀破坏已被确认为钢筋混凝土结构耐久性降低的首要因素。氯离子是海洋环境下引起钢筋锈蚀导致混凝土结构破坏的最主要因素。因此研究海洋环境下氯离子在混凝土的输运，对于海洋工程混凝土结构的耐久性设计意义重大，同时还可以带来可观的社会经济效益［1］。潮差区、浪溅区处于干湿交替的复杂环境中，是腐蚀劣化最为严重的区域，直接影响着海工结构的耐久性和使用寿命。所以本文重点对潮差区、浪溅区混凝土中的氯离子输运模型及仿真进行研究。

国内外许多学者对氯离子在混凝土中的输运进行了大量的研究［2-6］。金伟良等［7-8］指出混凝土孔隙水饱和度是影响氯离子扩散系数的重要因素；文献［9-10］研究发现氯离子在混凝土内的扩散系数与孔隙饱和度有关，饱和度越大，扩散系数越大；姬永生［11］通过对混凝土孔隙水饱和度的试验研究和机理分析，建立了混凝土孔隙水饱和度的定量计算公式，但是公式中存在一些参数，较难确定。

本文研究潮差区、浪溅区的氯离子在混凝土的输运，采用Hamilton型变分原理建立氯离子的输运模型。结合细观角度，建立了一个有效的孔隙水饱和度的定量计算公式。引入时间因素和孔隙水饱和度，对非饱和状态下氯离子的扩散系数进行修正。最后利用本文建立的氯离子的输运模型进行了数值模拟，并与相应的实验进行了对比，得出相应的结论。

1　氯离子输运的Hamilton型变分原理

潮差区和浪溅区的混凝土结构，由于海水水位的变化，长期处于干湿交替的复杂环境，其输运规律的实质是氯离子随溶液在非饱和多孔介质中的输运问题，对流和扩散是氯离子输运的主要方式［7］。应用功能转换原理和能量守恒定律，氯离子输运的Hamilton型变分原理可以表示为

式中，Πin为内能对时间的变化率，Πd为扩散能对时间的变化率，Πc为对流能对时间的变化率。Πin、Πd和Πc的变分式分别表示为

式中:R为气体常数，T为绝对温度，c0为标准态氯离子浓度，c为氯离子浓度，ccr为氯离子的临界浓度，D（s）为扩散系数（D是孔隙饱和度s的函数），v为渗流速度，t为时间。

胡海昌指出，检验变分原理的最好的方法是推导其驻值条件［12］。以下推导氯离子输运耦合动力学Hamilton型变分原理的驻值条件。

将Π变分，并令δΠ=0，可得

应用Green定理:

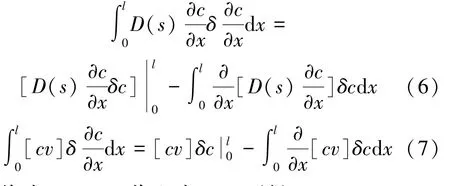
将式（6）、（7）代入式（5），可得

式（9）～（11）是氯离子输运耦合动力学Hamilton型变分原理的驻值条件。从浓度的耦合关系来看，式（9）反映了扩散过程与对流过程之间互为初始条件和边界条件的耦合关系。从孔隙饱和度的耦合关系来看，式（9）反映了混凝土孔隙处于非饱和状态下，扩散与对流过程的耦合效应。

2　非饱和孔隙中氯离子的扩散系数

文献［11］指出，混凝土耐久性能的退化由混凝土的孔隙水饱和度所决定。因此，应该首先对混凝土孔隙水饱和度定量计算进行研究。

混凝土孔隙水饱和度的表达式［11］:

式中:s为孔隙水饱和度，f（d）为孔隙密度函数，d为孔隙直径，w为水膜厚度，dk为开尔文直径，V混凝土的总孔隙率。

但是，孔隙密度函数f（d）很难由试验来确定，所以难以通过式（12）对混凝土孔隙水饱和度进行定量计算。

从细观角度，可以将混凝土中的孔隙分为骨料中的孔隙、水泥砂浆基质中的孔隙和界面过渡区的孔隙三部分。根据孔隙水饱和度的定义建立了新的混凝土孔隙水饱和度的计算公式:

式中:Vc、Va、Vitz分别为水泥砂浆基质中的孔隙率、骨料的孔隙率和界面过渡区的孔隙率，βc、βa、βitz分别为水泥砂浆基质中的孔隙水填充率、骨料的孔隙水填充率和界面过渡区的孔隙水填充率。

相比于砂浆基质和界面过渡区，骨料较为密实，具有很低的孔隙率，因此假定骨料不具有渗透能力。式（13）可以改写为

考虑到水泥砂浆基质中的孔隙率只与水灰比和水泥水化程度有关，则水泥砂浆基质中的孔隙率可以表示为［3-4］

则界面过渡区的孔隙率可以表示为

式中:W/C为水灰比，α为水化程度。

孔隙在非饱和状态下，氯离子的扩散系数受到时间因素和孔隙水饱和度的影响，所以非饱和状态下氯离子扩散系数可以由下式确定:

式中:D（s）为孔隙非饱和状态下氯离子的扩散系数，m为时间衰减因子，ηc和ηitz分别为水泥砂浆基质和界面过渡区的孔隙水饱和度对氯离子扩散的影响系数，Dp为饱和孔隙溶液中氯离子的扩散系数。

根据有效介质理论，水泥砂浆基质的孔隙水饱和度对氯离子扩散的影响系数可以表示为［4］

式中:n为待定参数。

文献［5，6，13］通过大量实验，测得界面的有效扩散系数是砂浆基质扩散系数的2～12倍，一般取7倍，即

3　数值模拟及验证

为了验证本文建立模型的正确性，采用有限元软件Comsol Multiphisics进行了数值模拟，并与相应的试验［14］进行了对比，得出相应的结论。

3.1有限元模型及参数

由于混凝土结构所处海洋环境的相对湿度较大，并且干湿交替周期较短。因此可以假设混凝土内部孔隙水填充率由表及里处于相同的分布状态，即βc=βitz。在饱水湿润状态下，混凝土试件孔隙水填充率为100%。在水分蒸发的干燥环节，混凝土试件孔隙水饱和度与外界环境湿度达到动态平衡。结合实验现场的气象资料，根据实验某天的干燥阶段相对湿度的取值，拟合出混凝土试件孔隙水填充率的曲线，如图1所示。

图1　干燥阶段相对湿度Fig.1 Relative humidity under dry phase

数值模拟的计算参数如下所示:时间衰减因子m为0.37；孔隙溶液氯离子扩散系数Dp为1.07× 10-10m2/s；水化程度α为0.8；水灰比W/C为0.4；表面氯离子浓度Cs为1.26%；渗流速度v为4.47× 10-10m/s；待定参数n为14.4。

根据试验对象，建立一个100 mm×50 mm二维矩形截面即可。利用Comsol Multiphisics，采用PDE模块描述氯离子迁移的对流—扩散场。计算条件参照文献［14］调研的现场资料。采用映射四边形网格对模型进行划分，网格长度为1 mm，共计5 000个单元。有限元模型网格划分图如图2所示。

3.2模型计算与数据分析

潮差、浪溅区干湿循环的过程中，湿润环节可以采用狄利克雷边界条件表示。此时可以认为表面氯离子浓度与饱和状态下的相同，即

干燥环节，氯离子不随水分的蒸发，滞留在侵蚀面表层，可以采用纽曼边界条件表示，即表面氯离子浓度梯度为0。假设氯离子入侵方向为x，则

利用上述模型参数对有限元模型进行计算，计算得到的结果与试验结果如图3所示。

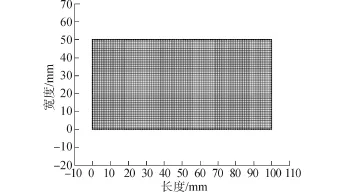
图2　有限元模型网格划分Fig.2 Finite element meshes for model

图3　不同位置氯离子的计算值与实测平均值的比较Fig.3 Comparison between calculated chloride profiles and measured average in concrete

由图3可以看出，干湿循环产生的氯离子累积效应使得氯离子在距离表面4 mm左右出现1个浓度峰值。是因为对流效应对氯离子输运的贡献高于扩散效应，混凝土试件浅层中的氯离子的补给速度往往高于氯离子由表层向深处扩散的速度，因此该区域出现一个峰值。

3.3潮差区、浪溅区与水下区氯离子计算值的对比

为了进一步定量的比较分析潮差区、浪溅区与水下区混凝土中氯离子的浓度。可以对水下区的氯离子的浓度进行有限元计算，并与潮差区、浪溅区的有限元计算结果进行对比分析。对比计算结果如图4所示。

由图4可知，潮差区、浪溅区的氯离子浓度始终大于水下区的氯离子浓度，并且潮差区、浪溅区的氯离子扩散速度也比水下区的氯离子扩散速度快得多。这就是潮差区、浪溅区钢筋锈蚀比水下区钢筋锈蚀严重得多的根本原因。

潮差区、浪溅区干湿交替作用的氯离子浓度始终大于水下区饱和状态下氯离子的浓度，符合氯离子运输的一般规律，从而进一步说明了模型的正确性。

图4　潮差区、浪溅区氯离子的计算值与水下区氯离子的计算值比较图Fig.4 Comparison between calculated chloride profiles under tide zone and splash zone condition and under underwater zone condition

4　结论

本文利用Hamilton型变分原理建立了氯离子输运模型；结合细观角度，建立了一个有效的孔隙水饱和度的定量计算公式；引入时间因素和孔隙水饱和度，对非饱和状态下氯离子的扩散系数进行修正；并采用有限元进行数值分析，得到了如下结论:

1）混凝土孔隙水饱和度，主要受孔隙率和填充率的影响；

2）本文提出的模型计算结果和实验数据吻合较好，并且符合氯离子运输的一般规律，证明了该模型的适用性。因此，本文提出的模型可以为潮差区和浪溅区混凝土结构的耐久性设计及服役寿命预测提供参考。

［1］郑晓燕.氯盐环境下混凝土结构性能劣化机理与试验［M］.北京:中国建材工业出版社，2014:3-6. ZHENG Xiaoyan.Performance degradation mechanism of concrete structure with the test under chloride environment ［M］.Beijing:China Architecture&Building Press，2014: 3-6.

［2］TANG Luping，LARS-OLOF N，BASHEER P A M.Resistance of concrete to chloride ingress:testing and modelling ［M］.London:Spon Press，2012.

［3］PIVONKA P，HELLMICH C，SMITH D.Microscopic effects on chloride diffusivity of cement pastes-a scale-transition analysis［J］.Cement and concrete research，2004，34（12）: 2251-2260.

［4］ZHENG Jianjun，ZHOU Xinzhu.Analytical solution for the chloride diffusivity of hardened cement paste［J］.Journal of materials in civil engineering，2008，20（5）:384-391.

［5］DELAGRAVE A，BIGAS J P，OLLIVIER J P，et al.Influence of the interfacial zone on the chloride diffusivity of mortars［J］.Advanced cement based materials，1997，5（3/4）:86-92.

［6］BRETON D，OLLIVIER J P，BALLIVY G.Diffusivity of chloride ions in the transition zone between cement paste and granite［C］//Interfaces between cementitious composites.London:E&FN Spon，1992:279-288.

［7］金伟良，袁迎曙，卫军，等.氯盐环境下混凝土结构耐久性理论与设计方法［M］.北京:科学出版社，2011:122-124. JIN Weiliang，YUAN Yingshu，WEI Jun，et al.Durability of concrete structure theory and design methods under chloride environment［M］.Beijing:Science Press，2011:122-124.

［8］金伟良，张奕，卢振勇.非饱和状态下氯离子在混凝土中的渗透机理及计算模型［J］.硅酸盐学报，2008，36 （10）:1362-1369. JIN Weiliang，ZHANG Yi，LU Zhenyong.Mechanism and mathematic modeling of chloride permeation in concrete under unsaturated state［J］.Journal of the Chinese ceramic society，2008，36（10）:1362-1369.

［9］CHAUBE R P，SHIMOMURA T，MAEKAWA K.Multiphase water movement in concrete as a multi-component system［C］//Proceedings of the 5th RILEM international symposium on creep and shrinkage in concrete.Barcelona，London:E&FN Spon，1993:139-144.

［10］延永东，金伟良，王海龙，等.干湿交替作用下氯离子在开裂混凝土中的输运规律［J］.中南大学学报:自然科学版，2013，44（5）:2060-2067. YAN Yongdong，JIN Weiliang，WANG Hailong，et al. Chloride transport in cracked concrete under wet-dry cycling condition［J］.Journal of central south university:science and technology，2013，44（5）:2060-2067.

［11］姬永生.钢筋混凝土的全寿命过程与预计［M］.北京:中国铁道出版社，2011:34-35. JI Yongsheng.Performance and prediction of reinforced concrete in full service life due to corrosion damage［M］. Beijing:China Railway Publishing House，2011:34-35.

［12］胡海昌.弹性力学的变分原理及其应用［M］.北京:科学出版社，1981. HU Haichang.The variational principle of elastic mechanics and its application［M］.Beijing:Science Press，1981.

［13］SHANE J D，MASON T O，JENNINGS H M，et al.Effect of the interfacial transition zone on the conductivity of portland cement mortars［J］.Journal of the American ceramic society，2000，83（5）:1137-1144.

［14］黄俊.潮差区水泥基材料氯离子侵蚀模拟试验的相似性研究［D］.杭州:浙江工业大学，2013. HUANG Jun.Study of similarity on simulation experiment considering chloride ion corrosion in cement-based material under the tidal zone［D］.Hangzhou:Zhejiang University of Technology，2013

［15］蔡荣，杨绿峰，余波.海洋潮汐浪溅区混凝土表面氯离子浓度计算模型［J］.海洋工程，2014，32（5）:25-33. CAI Rong，YANG Lufeng，YU Bo.Computing model for surface chloride concentration of concrete in marine tidal and splash zones［J］.The ocean engineering，2014，32 （5）:25-33.

［16］CRETE D.General guidelines for durability design and redesign［R］.The European Union-Brite Eu Ram III，Project No.BE95-1347.Probabilistic Performance Based Durability Design of Concrete Structures，2000.

本文引用格式：

赵昆璞，刘宗民，毛继泽.潮差区、浪溅区混凝土中的氯离子输运模型及仿真研究［J］.哈尔滨工程大学学报，2016，37（7）:950-954.

ZHAO Kunpu，LIU Zongmin，MAO Jize.Modeling and simulation of chloride transport in concrete in intertidal and splash zone conditions［J］.Journal of Harbin Engineering University，2016，37（7）:950-954.

Modeling and simulation of chloride transport in concrete in intertidal and splash zone conditions

ZHAO Kunpu，LIU Zongmin，MAO Jize
（College of Aerospace and Civil Engineering，Harbin Engineering University，Harbin 150001，China）

The intertidal and splash zones in dry-wet cycling complex environments are vulnerable to the most serious corrosion activity，which directly affects the durability and service life of maritime structures.In this study，we establish a model to describe the transport rule of chloride in concrete in intertidal and splash zone conditions.We based the chloride transport equations on the Hamilton principle and established an effective quantitative calculation formula to describe the degree of pore saturation based on the meso view.We modified the chloride diffusion coefficient by introducing a time factor and the degree of pore saturation.We simulated the migration of chloride in the concrete by the finite element method and compared the calculation results with the experimental data and the calculated value of chloride in the underwater zone.The calculation results agree well with the experimental data and conform to the chloride transport rule.These results prove that the model can provide a reference for durability design and for predicting the service life of concrete structures in intertidal and splash zone conditions.

tide zone；splash zone；chloride diffusion coefficient；transport model；degree of pore saturation

10.11990/jheu.201506086

TU528.1

A

1006-7043（2016）07-950-05

2015-06-29.网络出版日期：2016-05-27.

国家自然科学基金项目（50908059）；黑龙江省自然科学基金项目（E201415）；中央高校基本科研业务费专项资金项目（HEUCF160207）.

刘宗民（1976-），男，副教授，博士；毛继泽（1976-），男，教授，博士.

刘宗民，E-mail:liuzongmin@hrbeu.edu.cn.

网络出版地址：http：//www.cnki.net/kcms/detail/23.1390.u.20160527.1445.022.html