三杆张拉整体折展过程动力学分析

罗阿妮，李旭，李全贺，程建军，刘贺平

（哈尔滨工程大学机电工程学院，黑龙江哈尔滨150001）

三杆张拉整体折展过程动力学分析

罗阿妮，李旭，李全贺，程建军，刘贺平

（哈尔滨工程大学机电工程学院，黑龙江哈尔滨150001）

本文针对三杆张拉整体结构的折展问题，提出一种索驱动的方法。利用矩阵法分析，使用节点广义坐标和连接矩阵描述结构中各构件的位置和空间分布，建立结构数学模型；通过索构件长度协调变化，杆构件长度不变来分析结构的折展过程。在考虑构件弹性的情况下，对水平索为主动构件实现结构向轴线方向折叠的运动过程进行了动力学分析。通过仿真分析验证了此折叠方案的可行性。并对折展过程中构件的长度和内力的变化进行了分析，分析结果表明：张拉整体结构通过构件长度协调变化可实现折展功能，此方法可使用于三杆张拉整体单元以及以三杆张拉整体单元为基础的复杂张拉整体结构。

张拉整体；节点广义坐标；连接矩阵；构件内力；可展结构

张拉整体结构是一种由连续受拉的索和不连续的受压杆构件组成的自应力稳定结构［1］。结构质量较传统的可展结构轻，且折叠后体积紧凑［2］，因此，张拉整体结构的可展研究具有重要意义。

张拉整体结构转化为可展结构的研究中，折展方式和运动过程的动力学分析是两个重要方面。本文突破了以构件为研究对象的传统动力学模型构建方法，基于节点广义坐标［3-5］、连接矩阵、系统刚度矩阵［6-9］建立分析模型。为便于分析本文以三杆张拉整体［10-12］单元为基础进行折展方式的研究及运动过程的动力分析。

1　三杆张拉整体结构构建

三杆张拉整体结构如图1所示，由正三棱柱，下端面固定，各棱绕z轴逆时针旋转150°［3，10］得到。以棱柱下底面形心 o为原点，x轴由形心o指向节点1，z轴由下底面形心指向上表面形心。结构有6个节点、9根索、3根杆（细线表示索，粗线表示杆）。

1.1节点坐标

节点广义坐标矢量矩阵［10］:

其中

式中:r为棱柱底面节点构成三角形外接圆半径，h为棱柱的高度（见图1）。

图1　三杆张拉整体结构示意图Fig.1 Three-bar tensegrity structure diagram

1.2分析构件连接矩阵及构件矢量阵

连接矩阵的一行，代表系统的一个节点广义坐标与系统所有构件的关系（起点“-1”、终点“1”、无关“0”）。连接矩阵的一列代表系统的一个构件与系统所有节点广义坐标之间的关系［3-5］（起点“-1”、终点“1”、无关“0”）。

杆连接矩阵［10］为

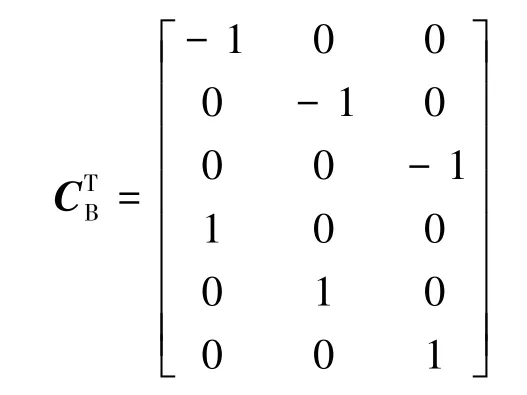
通过节点矩阵及杆连接矩阵可以得到杆的空间向量:

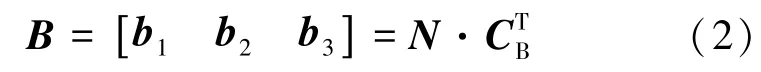
索的连接矩阵［10］为

通过节点矩阵及索连接矩阵可以得到索的空间向量:

对构件向量求模，可得到杆构件长度。

2　折展分析

2.1折展方式

改变杆构件或索构件的长度都可以促使结构展开和折叠。由于索构件长度容易改变，而且其柔性也降低了展收的难度。因此，选择杆构件长度不变，只调节索构件长度来促使结构折展。

具体有两种折叠方式:通过水平索主动缩短，斜索随动伸长，就可以使结构向轴线折叠为一束；通过斜索主动缩短，水平索随动伸长，就可以使结构向端面折叠。这两种折叠过程是相反的，文中选择水平索为主动索这一折叠方式进行分析。

2.2折展分析的方法

2.2.1节点位移

本文以节点为研究对象，对结构进行动力学分析。设结构总质量为m，将总质量等效到系统节点上。由于所有节点到达结构形心的距离相等，所以等效在六个节点上的质量相等，均为m/6。则结构的运动方程为［9］

令Δt为时间增量。根据中心差分公式［11］，得到此节点的加速度表达式:

进一步推导可得其速度表达式为

将式（5）、（6）代入式（4），经过整理后可以得到

由于索杆结构的振动过程中阻尼很小，对结构运动影响不大，可以忽略，因此式（7）可以改写为

由式（8）可以得到位移的增量Δδt:

这样就可以求出节点的新坐标:

根据上式得到的新的节点矩阵分析此时运动状态是否已达到折叠要求。

2.2.2节点受力分析

任意构件只与两个节点相连，构件只受轴向力作用［12］，单个构件受力如图2。

图2　构件受力分析图Fig.2 Member stress analysis

构件两端节点受力与位移关系如下:

式中:E为材料的弹性模量，A为构件横截面积，δi、δj分别为i与j节点的位移，Fi、Fj分别为i与j节点所受的力，lij为该构件的原始长度。将式（11）写成矩阵的形式:

将节点力与位移分为x、y、z三个方向:

式中:α、β、γ分别为力与位移在矢量方向上与三坐标轴的夹角。将式（11）的矩阵等号两边同时做成夹角矩阵的转置矩阵，通过结合式（12）～（14）可以得到

式中:矩阵 K称为刚度矩阵［9］，刚度矩阵是对称矩阵。

在对单个杆、索单元两个节点位移分析的基础之上，可以得到单元的刚度矩阵，在预应力已知的情况下可以得到节点位移。为了直接得到整个系统的位移需要知道体系的总刚度矩阵，这里引入协调矩阵T，协调矩阵是将某节点刚度矩阵内的元素放置在总体刚度矩阵对应的位置上，其余位置为0，其目的是为了将单元刚度矩阵的维数扩大到总刚度矩阵的维数，得到体系的单元刚度矩阵［9］:

将经过扩充后的所有单元刚度矩阵相加得到结构总体刚度矩阵:

式中:u是构件数目。通过系统总刚度矩阵，可以得到等式:

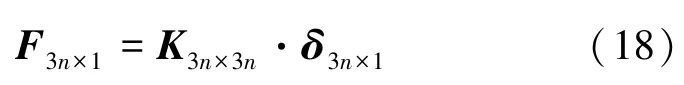
可以利用该式在节点位移已知的情况下求解此时系统节点受力情况。节点所受合力为

3　折展过程仿真分析

水平索收缩，斜索随动伸长，驱动结构向轴线折叠为一束。运动过程中，为了适应斜索长度随动变化，用弹簧替代斜索。设在运动的初始状态替代斜索的弹簧伸长量为0。

水平索上施加恒力来驱动结构运动，设杆的长度为10 m，初始位置时r为3 m，总质量为150 kg，每根水平索的驱动力大小为。弹簧刚度系数为1 000 N/m，杆的弹性模量Eb=2.06×1011Pa，杆的横截面积Ab=7.85×10-5m2。根据前面的分析，通过MATLAB编写程序对结构的折叠过程进行仿真分析。图3为仿真分析所获得的三杆张拉整体结构的运动过程仿真图。这一分析结果证明了收缩水平索驱动结构折叠的这一方案是可行的。

在结构运动过程中，构件长度和内力都是在不断变化的，构件的长度变化曲线如图4所示。

图3　结构折叠过程Fig.3 The folding process

图4　构件长度、速度、加速度变化曲线Fig.4 The length，velocity，acceleration curve

由图4（a）可知，在结构运动过程中，在考虑弹性变形的条件下，杆的长度也有所变化，但是由于杆的弹性模量相对较大，所以杆的长度变化很小。斜索一直被逐渐拉长，直到长度与杆长相等，因此斜索利用拉簧张紧既可。水平索作为驱动构件，它的长度随着结构运动不断变短。

从图4（b）发现，由于杆构件的长度变化微小，所以其长度变化速度的变化很小。斜索和水平索的长度变化速度都为先增大后减小，在运动结束时速度趋于0。比较而言，斜索的长度变化速度较平稳，而水平索长度变化要剧烈得多。

由图4（c）可知，水平索的长度变化加速度从运动开始时变化较小，接近结束时，其加速度迅速变大，其变化幅度较其他构件大好多倍。由于运动变化较为剧烈，所以应该通过一定的控制策略来减小水平索的长度变化加速度。在运动的终止段减小驱动力是一种可取的改进方案。

结构运动过程中，构件的受力变化如图5所示。由于水平索为驱动构件，其驱动力为定值，这里就没有分析。由于斜索由弹簧替代，在运动过程中一直伸长，因此其内力是逐渐变大的，图5也反映了这一变化规律。因此在设计此弹簧时，只要考虑运动起始点和终止点其长度值即可。

杆的内力波动幅度较大，这也说明其长度在运动过程中也是按此规律变化。杆构件的抖动，势必会引起整个结构在运动的过程中发生振动，因此张拉整体结构在运动过程中的抖动是不可避免的。当此类结构作为像星载可展结构等对振动有严格要求的机械设备来使用时，这一振动现象必须要进一步分析。

图5　构件内力变化曲线Fig.5 Internal force curves

4　结论

本文通过节点广义坐标和连接矩阵建立三杆张拉整体结构数学模型；介绍了通过收缩水平索促使结构折叠的方法，分别分析了在折展过程中节点的位移与受力变化。

通过分析，有以下结论:

1）提出通过收缩水平索，斜索随动伸长，促使结构收缩为一束这种结构折叠方法。

2）在折叠过程中，杆构件的抖动会引起整个结构在运动的过程中抖动。因此，此方法应用于对振动有严格要求的机械设备时，需对此振动现象进一步分析。

3）此折叠方法不止适用于三杆棱柱型张拉整体结构，对其他张拉整体可展结构也同样适用。

［1］FULLER R B.Tensile-integrity structures:United States，3063521［P］.1962-11-13.

［2］刘锡良，陈志华.一种新型空间结构-张拉整体体系［J］.土木工程学报，1995，28（4）:51-57. LIU Xiliang，CHEN Zhihua.A new type of space structurestensegrity systems［J］.Journal of civil engineering，1995，28（4）:51-57.

［3］SKELTON R E，OLIVEIRA M C.Tensegrity systems［M］. New York:Springer Science Business Media，2009.

［4］LUO Ani，SKELTON R E，LIU Heping，et al.Structure of the ball tensegrity robot［C］//Proceedings of IEEE International Conference on Robotics and Biomimetics.Paris，2014.

［5］GONZÁLEZ A，LUO A N，LIU H P.Construction of a unit cell tensegrity structure［C］//Proceedings of the 14th World Congress in Mechanism and Machine Science.Taipei，2015: 25-30.

［6］ZHANG Liyuan，LI Yue，CAO Yanping，et al.Stiffness matrix based form-finding method of tensegrity structures［J］. Engineering structures，2014，58:36-48.

［7］GUEST S D.The stiffness of tensegrity structures［J］.Institute of mathematics and its applications journal of applied mathematics，2011，76（1）:57-66.

［8］GUEST S.The stiffness of prestressed frameworks:a unifying approach［J］.International journal of solids and structures，2006，43（3/4）:842-854.

［9］孔令营.圆环张拉整体结构的构型及分析方法研究［D］.哈尔滨:哈尔滨工程大学，2015:62-67. KONG Lingying.The research on configuration and analytical method of torus-type tensegrity structures［D］.Harbin: Harbin Engineering University，2015:62-67.

［10］LIU Heping，LI Xu，CHENG Jianjun，et al.The folding course for the tensegrity basic unit［C］//Proceedings of the ASME 2015 International Mechanical Engineering Congress and Exposition.Houston，Texas，USA，2015.

［11］张幸锵，袁行飞.新型三棱柱张拉整体平板结构研究［J］.建筑结构，2011，41（3）:24-27，77. ZHANG Xingqiang，YUAN Xingfei.Research of a new triangular prism tensegrity plate structure［J］.Building structure，2011，41（3）:24-27，77.

［12］陈志华，史杰，刘锡良.张拉整体三棱柱单元体试验［J］.天津大学学报，2004，37（12）:1053-1058. CHEN Zhihua，SHI Jie，LIU Xiliang.Experimental study on triangular prism unit of tensegrity［J］.Journal of Tianjin university，2004，37（12）:1053-1058.

本文引用格式：

罗阿妮，李旭，李全贺，等.三杆张拉整体折展过程动力学分析［J］.哈尔滨工程大学学报，2016，37（7）:974-978.

LUO Ani，LI Xu，LI Quanhe，et al.Dynamic analysis of the three-bar tensegrity deployable structure［J］.Journal of Harbin Engineering University，2016，37（7）:974-978.

Dynamic analysis of the three-bar tensegrity deployable structure

LUO Ani，LI Xu，LI Quanhe，CHENG Jianjun，LIU Heping
（College of Mechanical and Electrical Engineering，Harbin Engineering University，Harbin 150001，China）

The string drive method is used to deploy the three-bar tensegrity structure.Based on the matrixes analysis，the mathematical model is built up with the generalized node coordinates and connectivity matrixes expressed positions and arrangements of members.The lengths of strings are adjusted with the bars＇length constant to deploy the structure.Based on the flexible of the members，shortening the level strings to make the structure fold towards its＇axis，it is analyzed that the dynamics of the structure.The simulation proved this deployable method is feasible. The changings of the lengths and inner forces of the members are given.The results show that adjusting the strings lengths could make the structure deployment.This method can be used in the three-bar tensegrity deployable structure and other structures which build up with the three-bar basic units.

tensegrity；generalized node coordinates；connectivity matrix；dynamic analysis；deployable structure

10.11990/jheu.201505069

TH113

A

1006-7043（2016）07-974-05

2015-05-25.网络出版日期：2016-05-13.

黑龙江省自然基金项目（11202128）；机器人技术与系统国家重点实验室（HIT）开放研究项目（SKLRS（HIT）2014 ZD 05，SKLRS（HIT）2015 M 01）.

罗阿妮（1978-），女，副教授，博士；刘贺平（1975-），男，副教授，博士.

刘贺平，E-mail:liuheping@hrbeu.edu.cn.

网络出版地址：http：//www.cnki.net/kcms/detail/23.1390.u.20160513.1344.006.html