Lebesgue-Stieljes积分理论的教学设计
让光林, 夏鹏程
(武汉大学数学与统计学院,武汉430072)
Lebesgue-Stieljes积分理论的教学设计
让光林,夏鹏程
(武汉大学数学与统计学院,武汉430072)
针对L-S积分理论作了一个4课时较完整的教学设计.教学内容包括R-S积分、L-S积分、分部积分公式(链式法则)和L-S积分在利率模型中的应用,同时统计了相应的教学反馈信息.
L-S积分; 分部积分公式(链式法则); 利率模型
1 引 言
目前,专业数学的课堂教学面临着改革的艰巨的任务.过去十年随着在校人数的绝对增加,数学课程的学习能力相对下降,数学教学的各个教学环节、教材编撰等都随之做了较大的改变.这一现象可以从复旦大学的《概率论》与中山大学的《概率论与数理统计》两套教材的变迁可见一斑,它们都在原来的基础上不同程度地降低了学习的难度,对学习难度较大的材料或者删减或者仅加以适当的解释而不给出严格的数学证明.这样处理毫无疑问是对的.另外一方面,随着现代科技的发展、国民对教育投入的比例不但加大以及师资力量的增强,具有很强的数学领悟和数学学习能力的学生数目与80、90年代相比绝对增加.这就要求我们必须在数学通识教育和数学精英教育之间进行平衡.一个好的办法是在普通生源里面通过二次(多次)选拔将非常有数学潜力的学生集中起来,为他们制定专门的教学大纲、配备优秀的师资,小班上课,因材施教.如武汉大学的数学基地班、弘毅班就具有鲜明的特色,我们充分利用自身的优势和国家层面的支持培养出了优秀的数学专业人才.具体到课堂教学,特别是高年级学生的课堂教学,他们己经具备了基本的分析和解决问题的能力.要充分利用选修课程课堂教学的灵活性,对教学材料进行适当的取舍、合理设计教学内容,以达到增加学生的知识点、拓宽学生的思维界限、帮助学生梳理已获得的知识线条,从而激发他们对数学学习和研究的兴趣.

2 R-S积分
设X是定义在某概率空间(Ω,F,P)上的随机变量,其分布函数为
F(t)=P(X(w)≤t),∀t∈R,

(1)


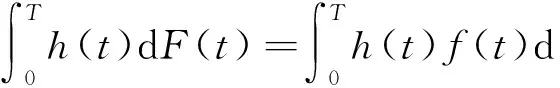
注1极限(1)给出的积分区域并不包含0,如考虑积分区域为 [0,T],则要加上一项h(0)(F(0)-F(0-)).很显然当F连续时,由于任意一点的测度为0,这时0点是否包含并不改变积分的值.


3 L-S积分
现设F是 [0,T]上的右连左极有限变差函数,(a,b]⊂[0,T],定义μF((a,b])=F(b)-F(a),则μF可以扩张成波雷尔域B([0,T])上的符号测度,并称之为由F生成的符号测度.对任意可测集A∈B([0,T])的示性函数1A,定义积分




例2设F是在内只取[0,T]有限多个值的某离散型随机变量的分布函数,

其中0

(2)


有


定理1设A,B均为[0,T]上的右连左极非降函数,则对任意t∈[0,T]有

(3)
证为了避免使用乘积测度空间,不妨假设A,B分别为独立随机变量X,Y的分布函数,其联合分布函数为A(u)B(v).根据分布函数的性质知
A(t)B(t)-A(t)B(0)-A(0)B(t)+A(0)B(0)=P(0 整理即得此定理得结论. 注2(3)式可以写成对称的形式 (4) 其中,ΔA(s)=A(s)-A(s-)表示A在s处的跳,而且上式最后一项和式至多只有可数多项.任意一个有限区间上右连左极有限变差函数A可以分解成两部分的和A =Ac+Aj,其中 (5) 定理2[2]设f是C1函数, A是有限变差函数,则f(A)也是有限变差,且下式成立 (6) 证显然f(x)=x结论成立.现设结论对f成立,并令g(x)=xf(x)由分部积分公式(3)知 对最后一行进行简单的整理即得定理对也是成立g(x)的.由此,我们知对所有的多项式定理结论成立.最后利用多项式逼近连续函数知结论对一切f∈C1均成立. 首先用纯跳增过程r={r(t)∶t∈[0,T]},r(0)=0来表示一无风险利率,r(ti)表示在时间区间[ti,ti+1)上的利率,i=0,1,…,n-1,0=t0 (7) 上式是中学生(甚至小学生)都知道的一个复利存款公式,实际上它是如下函数方程的唯一解: (8) 注意到,由非降函数r生成的测度只在{t1,t2,…,tn}诸点上有负荷,分别为 r(ti)-r(ti-1),i=1,2,…,n. 且Y(t2-)=1+r(t1), 而 =(1+r(t1))(l+r(t2)-r(t1))=(1+Δr(t1))(1+Δr(t2)). (9) 重复递推可知(7)是(8)的解. 接下来设r在[0,T]上连续变化,仍然用Y(t)表示初始存入1元到t时刻的资产.我们用逼近的方法计算Y(t).为此,将区间[0,r(T)]等分,对应区间的 [0,T]一个划分0=t0 (10) 由(7)知当 (11) 的解.实际上取f(x)=ex,则f′=ex,使用定理1有 (12) 由此知er(t)是方程(11)的解,后者即为连续复利模型,由此可知连续复利可以通过分段计利来逼近.具体的逼近性见定理3的证明. 一般情况下,利率函数不连续连续.这时可将r分解成纯跳和连续两部分的和,即(5)成立.设初始存入1元,X(t)表示t时刻本金加复利利息收入的和,结合方程(8)及(11),我们知X(t)应该满足如下积分方程 (13) 定理3方程(13)存在唯一解,且解可表示如下形式 (14) 证先证唯一性,设X1,X2是上述方程的两个有界解,则Z(t)=X1(t)-X2(t)满足方程 (15) 其中最后一个不等式使用了分部积分公式.反复利用上式,可得 |Z(t)|≤M(t)rn(t)/n!, 令n→∞由右连左极性质知对任意t∈[0,T],Z(t)=0. 对U,V使用分部积分公式得 本教案两次在武汉大学数学基地班、弘毅班选修课程——随机过程的教学中使用过,两次选课人数有25人.该课程安排在第7学期,从教学效果来看,4学时的教学内容对他们前期的积分理论的梳理有非常大的帮助,并澄清了一些模糊的概念,如积分的区间端点问题;对两种积分的区别的认识进一步加深;从课后反馈的信息得知很多学生对利率模型非常感兴趣,觉得很有趣.教学内容完成后,给每个学生发了一张类似[1]的muddiest卡片,让学生自行填写最迷糊的知识点和最有意思的知识点,其中有2人未填写.以下是相应的统计,后面的数字表示人次. 1.最迷糊的知识点:区间端点问题3; 例2. 1的R-S积分的存在性2;分部积分公式的左极限问题5;链式法则右边第三项的求和4;公式(6)3;U,V的分部积分公式的使用2. [1]Mosteller F.The Muddiest point in the lecture. On teachingand Learning, Harvard-Danforth Teaching Center Newsletter (April)[M]. Cambridge, MA:Harvard University, 1989. [2]Prottert P. Sochastic Integration and Differential Equations[M]. Berlin: Heidelberg Springer, 2005. [3]Yor M, Revue D.Continuous Martingale and Brownian Motion Series: Vol 293 Grundlehren der mathematischen Wissenschaften[M]. Hongkong: Springer, 1999. A Lecture for L-S Integration RANG Guang-lin,XIA Peng-cheng (School of Mathematics and Statistics, Wuhan University, Wuhan 430072, China) An L-S integration is given in detail, which is usually omitted in undergraduate courses. It contains R-S integration, L-S integration, integration by parts, chain rules and an application in interest rate model. Also some feedbacks from students for this lecture are listed. R-S integration; L-S integration; integration by parts; interest rate model 2015-11-09;[修改日期]2016-03-24 武汉大学2015教学改革项目(2015JG26) 让光林(1970-),男,博士,副教授,从事随机分析研究.Email:glrang.math@whu.edu.cn O211.1 C 1672-1454(2016)04-0085-06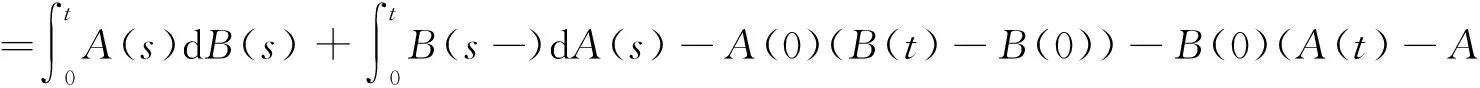
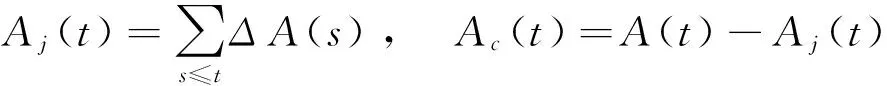


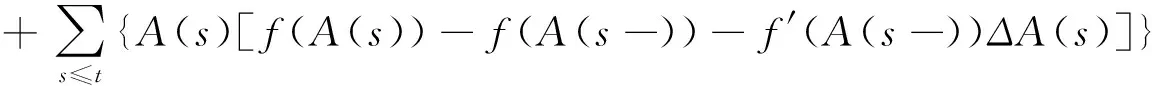

4 一个应用















5 总 结


