结合律在数项级数中的巧用
徐辉明
(浙江师范大学数理与信息工程学院,浙江金华321004)
结合律在数项级数中的巧用
徐辉明
(浙江师范大学数理与信息工程学院,浙江金华321004)
讨论结合律在无穷级数中的运用,并对2015年浙江省高等数学竞赛中一道竞赛题进行了分析和探讨.
级数; 收敛; 结合律
1 引 言
众所周知,有限个实(复)数的加法运算满足交换律和结合律,但在无穷级数中,交换律和结合律一般不成立,要在数项级数中运用交换律和结合律,需要满足一定的条件. 在数学分析教材中,下面两个定理是常见的.
定理1[1]在收敛级数的项中任意加括号,既不改变级数的收敛性,也不改变级数的和.
定理2[1]若级数∑un绝对收敛,且其和为S,则对该级数的项任意重排后所得的级数也收敛于S.
由此可见,收敛级数的项之间适用结合律,绝对收敛级数的项之间满足交换律.
在研究无穷级数的某些问题时,若能巧用结合律对级数的项进行分组,将有助于问题的解决. 本文中,我们将通过实例展示结合律在研究级数收敛性问题中的运用,并对2015年浙江省高等数学竞赛中一道竞赛题进行分析和探讨.
2 运用结合律研究级数的敛散性
由定理1可知,若级数收敛,则可适用结合律,下面的例子说明一般情形下结合律并不成立.

(-1+1)+(-1+1)+…+(-1+1)+…,
所得到的级数收敛.
上述例子表明,发散级数通过适当的方式加括号后有可能收敛. 但对于正项级数,这样的情形就不会发生.
命题1在正项级数的项中任意加括号,不改变级数的敛散性.

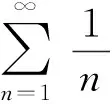

(1)
级数(1)的第k个部分和(k>1)是

命题2对级数
(2)
加括号,得到级数
(u1+…+un1)+(un1+1+…+un2)+…+(unk-1+1+…+unk)+…,
(3)
如果级数(3)的每个括号中各项符号相同,则当级数(3)收敛时,级数(2)也收敛.

|Snk-A|<ε.
(4)

注1命题2是文献[1]中的一个习题,为了内容的完整性,我们在这里给出了证明.


(5)

(6)
由命题2,只需证明级数(6)收敛.
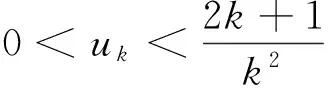
另一方面,

而

根据交错级数的Leibniz判别法知级数(6)收敛.

发散.

∀ε>0,∃N>1,当n>N时,∀正整数p,都有

(7)

+[(nm+1)anm+1+…+nm+1anm+1]+…

其中


也可采用下列的分组方法:
第1组从n+1项到2n项,第2组从2n+1项到4n项,……,第m组从2m-1n+1项到2mn项,……,于是,有
+[(2m-1n+1)a2m-1n+1+…+2mna2mn]+…
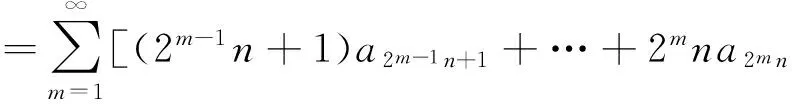
其中
(2m-1n+1)a2m-1n+1+…+2mna2mn<2mn(a2m-1n+1+…+a2mn)


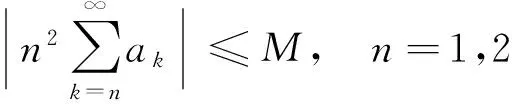
利用上述分组方式,通过进一步分析还发现,可以对条件或者结论进行改进,将条件减弱或者结论加强,得到如下的




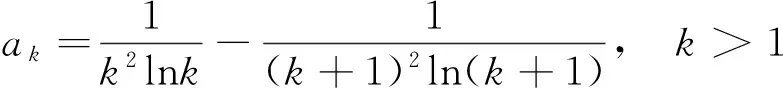
[1]华东师范大学数学系. 数学分析(下册)[M]. 4版. 北京:高等教育出版社,2010.
[2]王泓博. 一道数学竞赛题的探讨[J]. 大学数学, 2015, 31(1):102-104.
[3]薛凌霄,李德新. 一类级数求和的推广[J]. 大学数学, 2015, 31(3):86-89.
Application of the Associative Law in Series
XU Hui-ming
(College of Mathematics, Physics and Information Engineering, Zhejiang Normal University,Jinhua Zhejiang 321004, China)
The author discusses the application of the associative law in series, analyses and studies a question of the competiton of advanced mathematics in Zhejiang Province in 2015.
series; convergence; associative law
2015-09-23;[修改日期]2016-04-07
国家自然科学基金(11271124, 11271332);浙江省自然科学基金(LY14A010013, LY16A010004)
徐辉明(1963-),男,博士,教授,从事多复变函数论研究.Email:xhm@zjnu.cn
O173.1
C
1672-1454(2016)04-0123-04

