美国Putnam数学竞赛中两道行列式证明题的泰勒公式解法

李　静

(解放军理工大学理学院，南京211101)



美国Putnam数学竞赛中两道行列式证明题的泰勒公式解法

李静

(解放军理工大学理学院，南京211101)

介绍了美国Putnam数学竞赛中两道行列式证明题的分析证明方法.选取行列式中的某个参数(常数)为变量，使得行列式可设为该变量的多项式，然后分别计算函数值和各阶导数值，进而利用泰勒展式即可计算出行列式的值.

泰勒公式； 行列式； 变量与常数

1　引　　言

泰勒公式是微积分学的重要内容[1]，其作用是将一般的可导函数展开为多项式或者表示为幂级数，将复杂的函数值计算转化为简单的多项式计算，因而在近似计算、工程技术中有着广泛的应用[2-3].特别地，当一个多项式以其他形式出现时，利用泰勒公式就可以将该多项式进行化简，从而便于理解，在有些情况下也更易于计算.

本文考察美国Putnam数学竞赛中两道关于行列式的证明题[4]，其基本思路是利用初等变换及行列式的性质将行列式化为易于计算的形式.注意到，这两道试题中的行列式都含有多个参数(字母记号)，可将其视为以其中某个参数(字母记号)为变量的多项式，因此，利用泰勒公式有可能简化行列式的计算.

2　预备知识及两道竞赛题的解法

首先介绍行列式的求导法则.今有n阶行列式D=∑(-1)tap11ap22…apnn,其中各元素aij是某个变量的可导函数，则行列式的一阶导数应为

D′=∑(-1)t(a′p11ap22…apnn+ap11a′p22…apnn+…+ap11ap22…a′pnn)

=∑(-1)ta′p11ap22…apnn+∑(-1)tap11a′p22…apnn+…+∑(-1)tap11ap22…a′pnn.

表示成行列式形式如下

(1)

行列式的求导法则就是先对行列式逐列求导其它列不变然后再对n个行列式求和，类似地也可进行逐行求导[5].下面给出这两道竞赛题的新证法.

例1(1940年第3届Putnam数学竞赛)求证行列式

(2)

能被kn-1除尽，并求其他因子.

分析行列式中的k,ai(1≤i≤n)都是常数，但题目是判断关于k的因子，所以把k看作变量，其余的都作为常数.最简单的2阶行列式情形，可直接按对角线法则计算

(3)

显然可以被k2-1除尽.注意到等号右边正好是关于k的多项式，很容易联想到，微积分学的泰勒公式正是把满足条件的函数展开成幂函数.

证该行列式可看做以k为自变量的n次多项式，其余ai(1≤i≤n)均看作常数，该多项式函数在实数域内连续且含有任意阶导数，由泰勒展式

(4)

下面考察不同次幂的系数，主要过程就是计算各阶导数.由行列式求导法则，一阶导数为

再把以上各n阶行列式分别按第1,2,…,n列展开，可降为n-1阶

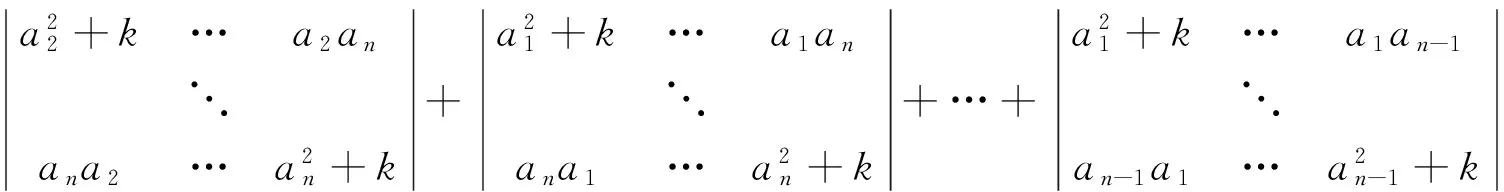
(5)

再求原行列式的2阶导数，即对(5)式的变量k求导，每个行列式可化为n-1个n-2阶行列式(形式也不变)相加，从而2阶导数是n(n-1)个n-2阶行列式之和.继续求导直到n-2阶，应为n(n-1)…3个2阶行列式相加，而每个行列式的形式均类似(3)式的左边(当然也与原式一致).直到n-1阶导数，应为n(n-1)…3·2=n!个1阶行列式相加，其中1阶行列式分别为

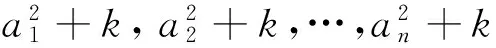
所以以上每一个行列式的系数为(n-1)!.最后的n阶导数肯定是0次多项式.

(6)

D(n)(k)=n!.

(7)

代入k=0可得各项系数

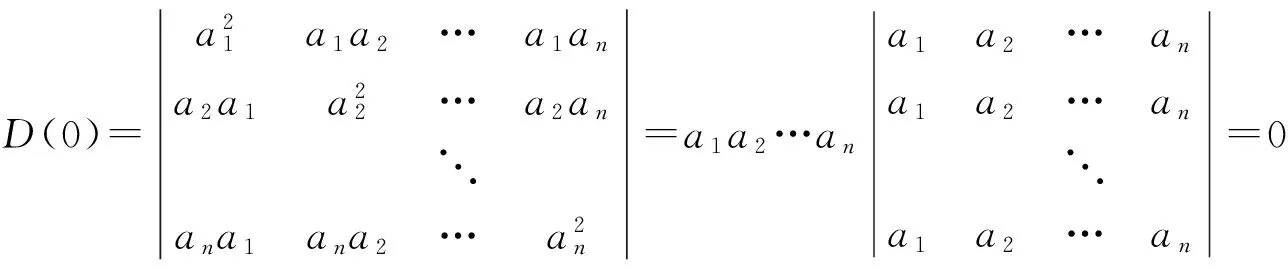
(8)

(9)

……

D(n-2)(0)=0，

D(n)(0)=n!，

于是

(10)

所以原行列式可被kn-1除尽.

例2(1951年第11届Putnam数学竞赛)如果a,b,c,d,e,f皆为实数，求证行列式

(11)

是非负的.

分析因为四阶行列式已没有对角线法则，想直接按定义计算出结果并不容易.该行列式包含12个非零元，每个元素的地位相似，出现且只出现了两次，那么行列式就可以表示为某个变量的2次函数.

证不妨设行列式是仅以a为自变量的2次多项式，其他变量相当于常数，由泰勒展式可得

(12)

下面就依次求各项系数，先求行列式的各阶导数.由行列式求导法则可知

(13)

行列式按列展开可得

(14)

继续求导

(15)

于是各项系数应为

(16)

(17)

g″(0)=2f2.

从而原行列式可表示为

g(a)=(be-cd)2-2af(be-cd)+a2f2=(be-cd-af)2.

显见

g(a)≥0.

3　结　　论

本文利用泰勒公式给出了两道关于行列式的Putnam竞赛题的一种简单证明.证明的关键步骤是选择恰当的参数，视行列式为该参数的多项式，这一过程可称为常量变量化，从而可利用微积分中对变量问题的处理方法解决行列式的计算问题.一般说来，选取变量的基本原则是要相应的多项式的次数尽可能低且有关行列式易于计算.

[1]同济大学数学系.高等数学(上册)[M]. 6版. 北京：高等教育出版社，2007.

[2]时统业，谢井，李鼎.论泰勒中值定理“中间点”的性质[J]. 大学数学，2012，28(4)：120-123.

[3]李井刚，朱晓临，王子洁.一种基于随机Taylor展开式的随机微分方程数值解法[J]. 大学数学，2013，29(4)：44-51.

[4]刘裔宏,等译，普特南数学竞赛试题(1939-1980) [M]. 长沙：湖南科学技术出版社，1983.

[5]华东师范大学数学系. 数学分析(上册) [M].4版.北京:高等教育出版社，2010.

Application of Taylor Expansion to the Calculation of Two Determinants Arising from William Lowell Putnam Competition

LI Jing

(College of Science , PLA University of Science and Technology , Nanjing 210007, China)

The paper introduces a new calculation of two determinants arising from the William Lowell Putnam Competition, by using the Taylor expansion in Calculus. With a properly chosen parameter, the determinants are regarded as polynomials with respect to the parameter. The determinants are figured out by using the Taylor expansion, when the determinants and their derivatives of different orders evaluated at a specified point are calculated.

Taylor expansion; determinant; variablization

2016-02-07；[修改日期]2016-05-06

解放军理工大学校级教育教学课题GJ1507038

李静(1980-),女，硕士，讲师，从事非线性动力学研究. Email：lj2003lover@163.com

O151.21

C

1672-1454(2016)04-0103-04