拉马努金等式的证明及推广
李尧其
(上海师范大学数理学院,上海200234)
拉马努金等式的证明及推广
李尧其
(上海师范大学数理学院,上海200234)
对于拉马努金等式,本文首先应用数列极限的方法给出其收敛性的证明.再结合式中多重根号嵌套的结构,通过构造函数方程,给出一个推广的结果.并将这种方法推广到一般形式,最后得到了此类极限的收敛性的一般判别法.文中使用的方法,为无穷根号形式的极限问题提供了系统化思路,丰富了极限的表达形式.
拉马努金等式; 极限; 收敛性; 函数方程
1 引 言
拉马努金(Ramanujan,1887-1920)是印度历史上极其伟大的数学家.他自学成才,尤其痴迷数论,思维极有跳跃性.拉马努金1887年生于印度东部的埃德罗,10岁进入中学,接触了正式的数学教育,并很快展现出很高的数学天赋.1913年,拉马努金给剑桥大学三一学院的哈代(G.H.Hardy,1840-1928)写信,报告自己的数学研究成果,他的数学天才由此受到学术界重视.拉马努金一生贫困,33岁便英年早逝,死后留下5个笔记本.时至今日,藏在这些笔记本中的数学思想与方法依然在被不断挖掘出来,并且应用到很多前沿领域.以下便是拉马努金发现的众多令人匪夷所思的等式中的一个

上式出自拉马努金数学笔记的第289题,称作拉马努金等式.拉马努金常凭直觉进行推导,笔者未见到拉马努金本人对这个等式的严格证明.本文分析了拉马努金等式的结构,分别应用数列极限、函数方程、函数列得到几种不同的证明方法以及推广结果.
2 基于数列极限的证法
容易验证,对于自然数n,有





3 利用函数方程作推广
初看拉马努金等式的结构,往往觉得证明无从入手.由于多层根号嵌套的形式,容易联想到以下这个结论

它和拉马努金等式的形式很接近,若是直接套用它的证法,却对拉马努金等式无效.通过以上的分析可以看出,同样是利用递推数列,转换递推方式,便能得到完全不同的结果.但是如果事先不知道原式等于3,那么证明过程将很难想到.利用函数方程的思路,又有了以下的方法.
令


当x>1时,有

另一方面

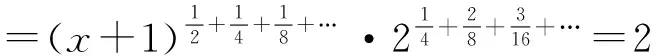

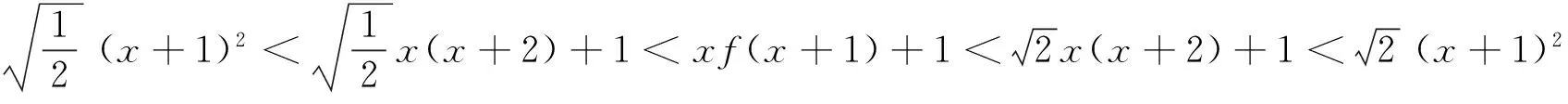
即

亦即

重复上述步骤可知,对于任何自然数n,有

令n→∞即可得到f(x)=x+1,从而f(2)=3,拉马努金等式成立.


由于函数方程并没有统一的解法,从f2(x)=1+xf(x+1)得出f(x)=x+1更多靠观察,或者拉马努金所说的“直觉”.证明过程中的不等式运用是非常巧妙的,至于x>1的限制是为了保证不等式成立,但1未必是最佳估计.
4 构造函数列
将数列和函数方程的思路相结合,又可以得到另一种证法.




另一方面

以下估计f(x)和x+1的距离.设δ(x)=x+1-f(x),则有0≤δ(x)<1. 由
f2(x)=1+xf(x+1)
得

从而对于任何有限的正数x,有

故

即δ(x)=0.则f(x)=x+1.f(2)=3. 拉马努金等式得证.
5 同敛态数列的构造

令




=…
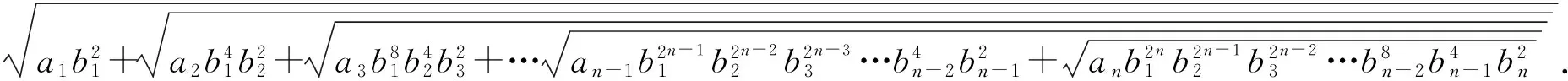

此外,还有等式
成立.








6 结 论
对于拉马努金等式,最容易想到的证明方法是利用数列极限.本文在这种方法的基础上,将其推广到一般的函数形式,这是一个自然的、也是重大的拓展.对于本文第五节中给出的一组同敛态数列,若此两个数列的极限果真有某种定量关系,则可由此轻易得到很多形如拉马努金等式的结果.
鉴于连分数理论的发展,笔者猜想形如拉马努金等式的“连根式”也会有一整套理论值得探讨.目前尚未见到这方面的专门研究.这无疑将是对数论问题的一种有益的补充和完善.
[1]华东师范大学数学系.数学分析(上册)[M]. 4版.北京:高等教育出版社,2010.
[2]刘培杰,等.超越吉米多维奇:数列的极限[M].哈尔滨:哈工大出版社,2009.
[3]罗伯特·卡尼格尔.知无涯者——拉马努金传[M]. 胡乐士、齐民友译.上海:上海科技教育出版社,2002.
The Proof and Generalization of Ramanujan’s Equation
LI Yao-qi
(Institute of Mathematical ,Shanghai Normal University,Shanghai 200234,China)
For the Ramanujan’s Equation,we give the proof of convergency by sequence limit firstly.Then construct a function equation for the square roots,and show a wider conclusion.In the end,we generalize the method to the general situation,and give a criterion for this kind of limit.The discuss in this article give a unitive train of thought of infinite square roots,and supplement the expressions of limit.
Ramanujan’s Equation; limit; convergency; function equation
2015-08-18;[修改日期]2016-05-19
李尧其(1994-),男,在读硕士,从事微分方程研究.Email:965156745@qq.com.
O171
C
1672-1454(2016)04-0118-05

