带一个形状参数的有理三次三角Bézier曲线

樊　文,　洪　玲，　邢　燕

(合肥工业大学数学学院，合肥230009)



带一个形状参数的有理三次三角Bézier曲线

樊文,洪玲，邢燕

(合肥工业大学数学学院，合肥230009)

构造了带一个形状参数的有理三次三角Bézier曲线，它不但具有传统三次有理Bézier曲线的几何性质，而且比传统有理Bézier曲线具有更灵活的形状调整能力.讨论了两段有理三次三角Bézier曲线的G1和C2拼接条件，并给出了这类曲线的应用.

有理三次三角Bézier曲线； 形状参数； 几何连续

1　引　　言

Bézier曲线是一个最基本的建模工具，被广泛应用于计算机辅助设计(CAD)和计算机辅助几何设计(CAGD)中.由于伯恩斯坦基函数的特殊性，Bézier曲线具有一些良好的性质.然而，由于多项式本身性质，很难产生所需要的曲线、曲面的形状.三角多项式在电子或医学领域的重要性是众所周知的.近几十年，三角多项式曲线和三角样条函数在CAGD中也得到关注和广泛应用，特别是在曲线的设计领域中[1-8].Bézier曲线不能精确表示圆锥曲线，三角Bézier曲线则可以精确表达圆锥曲线.要调整Bézier曲线的形状，只能通过改变其控制顶点.引入形状参数，对伯恩斯坦基函数进行扩展，近十几年来被广泛研究[6-13].带参数的样条曲线在交互式形状生成中起着重要的作用[1].文献[2]介绍了C1的带一个形状参数的二次三角多项式，这类曲线中的形状参数可以很好地控制所生成曲线的形状，比传统二次B样条更接近控制多边形.文献[3]介绍了带多个形状参数的二次三角样条曲线，这种曲线类似于三次B样条曲线，当取不同的参数值，可以达到不同阶的参数连续.文献[4]和文献[5]分别提出了C2连续的分段二次三角多项式曲线和带一个全局形状参数的三次三角多项式曲线.文献[6]介绍了带两个形状参数的三次三角Bézier曲线.文献[7]对带一个形状参数的三次三角Bézier曲线的形状进行了分析.随着对Bézier曲线的不断深入研究，有理Bézier曲线越来越受到曲线设计人员的青睐.有理Bézier曲线不仅可以表示非有理Bézier曲线，而且可以表示圆锥曲线.本文在文献[7]的基础上，讨论了带一个形状参数的有理三次三角Bézier曲线的性质、拼接和应用.

2　有理三次三角Bézier曲线

定义1[7]对任意的t∈[0,1]，带一个形状参数λ∈[-2,1]的三次三角基函数定义如下：

(1)

图1　三次三角基函数

定义2带一个形状参数的有理三次三角Bézier曲线定义如下

(2)

其中pi(i=0,1,2,3)为曲线的控制顶点，w0,w1,w2,w3为正权因子，bi(t)(i=0,1,2,3)是(1)式中定义的基函数.

当w0=w1=w2=w3=1时，有理三次三角Bézier曲线f(t)转化为非有理Bézier曲线.有理Bézier曲线可以通过权因子标准化，即通过形状不变因子k1,k2：

调整内部两个权因子w1,w2大小，将w0,w3化为1，保持原来图形不变[14,15].任意的有理三次Bézier曲线都可以转化为首尾权因子为1的标准形式.为了讨论方便，下文的讨论是建立在w0=w3=1的基础上.

定理1有理三次三角Bézier曲线的性质

(a)端点性质

(b)对称性

f(t;λ,p0,p1,p2,p3)=f(1-t;λ,p3,p2,p1,p0).

(c)几何不变性

f(t;λ,p0+q,p1+q,p2+q,p3+q)=f(t;λ,p0,p1,p2,p3)+q,

f(t;λ,p0*T,p1*T,p2*T,p3*T)=f(t;λ,p0,p1,p2,p3)*T.

其中q∈R2为任意向量，T为2×2的变换矩阵.

(d)保凸性

生成曲线包含在由控制顶点pi(i=0,1,2,3)形成的凸包中.

3　曲线的拼接

两段有理三次三角Bézier曲线

和

可以方便地进行G1,G2拼接.

当q0=p3时，两条曲线达到G0连续.

3.1G1光滑拼接

定理2两段有理三次三角Bézier曲线G1光滑拼接的充要条件是

(i)p3=q0,

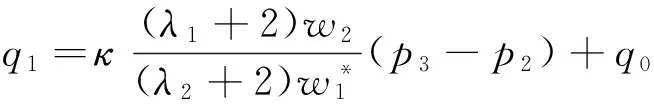
当κ=1时，则满足C1光滑拼接.

证两段有理三次三角Bézier曲线要达到G1光滑拼接，根据文献[14]，有充要条件

由定理1中的端点性质，即可证明.

3.2G2光滑拼接

定理3两条有理三次三角Bézier曲线G2光滑拼接的条件除了满足G0,G1条件外，还需满足曲率连续条件，即

特别地，当p3=q0,f′1(1)=f′2(0),f″1(1)=f2″(0)时，曲线满足C2连续.

由定理1知，有理三次三角Bézier曲线的二阶导公式很复杂，为了简化计算，这里只讨论λ1=λ2=1时，达到C2连续的情况.达到C2连续时要求：

(a) G1光滑拼接　　　　　　(b) C1光滑拼接 　　　　　　(c) C2光滑拼接图2　两段有理三次三角Bézier曲线的光滑拼接

4　有理三次三角Bézier曲线的应用

4.1有理三次三角Bézier曲线表示椭圆

即椭圆的参数方程，对应的标准方程为

当t∈[0,4]时，可以表示整个椭圆.当a=b时，则表示一个圆.

4.2有理三次三角Bézier曲线造型

引入形状参数，对伯恩斯坦基函数进行扩展，可以有效地调整曲线的形状.图3(a)是用文献[7]提出的带一个形状参数的三次三角Bézier曲线生成的花瓣图案，从内向外形状参数分别取：-2,-1,-0.5,0,0.5,1，由图可知，三次三角Bézier曲线不仅可以位于传统Bézier曲线的下方，也可以位于传统Bézier曲线上方进行形状调整.图3(b)和(c)绘制的是本文的有理三次三角Bézier曲线，其中(b)中权值为w0=w3=1,w1=w2=2，(c)中权值w0=w3=1,w1=w2=6.从内向外形状参数同样分别取为λ=-2,-1,-0.5,0,0.5,1.

当w0=w1=w2=w3=1时，有理三次三角Bézier曲线退化为文献[7]中的三次三角Bézier曲线，所以图3(a)也可看作是有理三次三角Bézier曲线4个权值均取1时的情形.可见，对有理三次三角Bézier曲线形状的调整，不仅具有文献[7]中曲线的性质，而且可以更逼近控制多变形.

(a) w0=w1=w2=w3=1　　(b) w0=w3=1,w1=w2=2　　(c) w0=w3=1,w1=w2=6图3　有理三次三角Bézier曲线的花瓣造型

5　结　　论

本文主要研究了带一个形状参数λ的有理三次三角Bézier曲线，这类曲线不仅具有传统有理三次Bézier曲线的几何性质，还可以精确表示圆锥曲线.本文讨论了两段有理三次三角Bézier曲线的光滑拼接条件，还应用它设计了花瓣形状.相信有理三次三角Bézier曲线将会被曲线设计人员广泛取使用.

[1]Bashir U, Abbas M, Ali J M. TheG1,G2rational quadratic trigonometric Bézier curve with two shape parameters with applications [J]. Applied Mathematics and Computation, 2013, 219(20): 10183-10197.

[2]Han X. Quadratic trigonometric polynomial curves with a shape parameter [J]. Computer Aided Geometric Design, 2002, 19(7): 503-512.

[3]Wu X, Han X, Luo S. Quadratic trigonometric spline curves with multiple shape parameters[C]∥Computer-Aided Design and Computer Graphics, 2007 10th IEEE International Conference on. IEEE, 2007: 413-416.

[4]Han X. Piecewise quadratic trigonometric polynomial curves [J]. Mathematics of computation, 2003, 72(243): 1369-1377.

[5]Han X. Cubic trigonometric polynomial curves with a shape parameter [J]. Computer Aided Geometric Design, 2004, 21(6): 535-548.

[6]Han X A, Ma Y C, Huang X L. The cubic trigonometric Bézier curve with two shape parameters [J]. Applied Mathematics Letters, 2009, 22(2): 226-231.

[7]Han X A, Huang X L, Ma Y C. Shape analysis of cubic trigonometric Bézier curves with a shape parameter [J]. Applied Mathematics and Computation, 2010, 217(6): 2527-2533.

[8]邬弘毅, 陈晓彦. 多形状参数的三次非均匀三角多项式曲线[J]. 计算机辅助设计与图形学学报, 2006, 18(10): 1599-1606.

[9]邬弘毅, 夏成林. 带多个形状参数的Bézier曲线与曲面的扩展[J]. 计算机辅助设计与图形学学报, 2006, 17(12): 2607-2612.

[10]刘植, 陈晓彦, 江平. 带多形状参数的广义Bézier曲线曲面[J]. 计算机辅助设计与图形学学报, 2010,22(5): 838-844.

[11]刘植, 檀结庆, 陈晓彦. 三角域上带形状参数的三次Bézier曲面[J]. 计算机研究与发展. 2012, 49(1): 152-157.

[12]翟芳芳. 带两个形状参数的五次Bézier曲线的扩展[J]. 大学数学. 2012, 28(3): 59-63.

[13]王青芳, 陈晓彦, 柏凯, 任淼. 一类新的拟Bernstein-Bézier曲线[J]. 大学数学. 2015, 31(2), 26-32.

[14]施法中. 计算机辅助几何设计与非均匀有理 B 样条: CAGD & NURBS [M]. 北京：北京航空航天大学出版社, 1994.

[15]Farin G.Curves and Surfaces for CAGD, A Practical Guide [M]. 3rd Ed. Boston: Academic Press, 1993.

Rational Cubic Trigonometric Bézier Curves with One Shape Parameter

FAN Wen,HONG Ling,XING Yan

(School of Mathematics, Hefei University of Technology, Hefei 230009,China)

The rational cubic trigonometric Bézier curve with one shape parameter not only inherits the geometric properties of the traditional cubic rational Bézier curve, but also provides a more flexible control on the shape of the curve than the traditional Bézier curve does. The G1and C2composition conditions of two segments of rational cubic trigonometric curves have been discussed. The class of curves can represent ellipses and design curves and patterns.

rational cubic trigonometric Bézier curves; shape parameter; geometric continuity

2016-01-20；[修改日期]2016-04-08

国家自然科学基金项目(U1135003，61472466)，安徽省自然科学基金项目(1308085MA09)，中央高校基本科研业务费专项经费(JZ2015HGXJ0175)，合肥工业大学科学研究发展基金项目(J2014HGXJ0067)

樊文(1984-)，男，硕士，从事计算机辅助几何设计. Email：415086199@qq.com

TP391

A

1672-1454(2016)04-0030-05