Liu系统的Lyapunov维数估计

韩雪琼,　柏晓明

(合肥工业大学数学学院，合肥230009)



Liu系统的Lyapunov维数估计

韩雪琼,柏晓明

(合肥工业大学数学学院，合肥230009)

基于Leonov提出的Lyapunov 维数理论，通过构造合适的Lyapunov函数,给出了Liu系统不变集的Lyapunov维数估计式.最后并给出了Liu系统混沌吸引子的Lyapunov维数估计.

维数理论； Lyapunov函数； Lyapunov维数； Liu系统

1　引　　言

随着混沌系统的大量发现，其吸引子的动力学行为受到国内外研究者的广泛关注，其中一个非常重要的问题是刻画混沌吸引子的维数，因为它反映了吸引子结构的复杂性和几何特征.其中一个就是Lyapunov维数,它由Kaplan和Yorker提出后[14]一直是人们的研究热点.2002年，基于Lyapunov函数方法俄罗斯院士Leonov系统地发展了一套估计该维数的理论.应用该理论估计混沌系统Lyapunov维数的关键在于构造恰当的Lyapunov函数.最近通过构造各种不同Lyapunov函数他巧妙地给出了Lorenz系统[1]、Chen系统、Lü系统、Tigan系统、Yang系统的Lyapunov维数估计.2004年刘崇新等人发现了一个含平方项的三阶连续自治混沌系统-Liu混沌系统[6],随后该系统的动力学行为受到了大家的极大关注[9-13].然而其吸引子维数估计却未知，本文应用Leonov理论给出Liu系统吸引子的Lyapunov维数估计.

2　Lyapunov维数吸引子

考虑一个微分方程

(1)

其中f:Rn→Rn, 令σ1(X(t,x0)≥…≥σi(X(t,x0))>0为其变分方程基本解矩阵X(t,x0)奇异值.

定义1[7]点x0处的Lyapunov指数定义为

定义2在点x0的Lyapunov维数的定义为

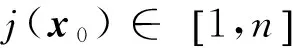
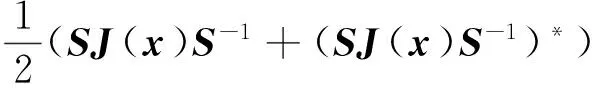
(2)

3　主要定理: Liu系统的Lyapunov维数

考虑下列的Liu系统

(4)

其中a>0,b>0,c>0,d>0,h>0.利用定理1和定理2, 本文给出了Liu系统的维数估计.

定理3对a和d，如果满足下列不等式

(5)

(6)

dc+2a(h-c)>0,

(7)

ab>d(a+d),

(8)

则系统(4)不变集KLyapunov维数满足

(9)

(10)

的特征值为

其中 γ=2β+d-a，

容易看出λ1≥λ2≥λ3.

其中

其中μ1,μ2,μ3,μ4为待定参数.根据定理1就必须有如下不等式成立:

(11)

即(c1) 选取适当的μ1,μ2,μ3,μ4,使

(12)

(c2) 存在s∈[0,1), 使

(13)

要使(12)式成立,故需选取适当的μ1,μ2,μ3,μ4使如下不等式组成立

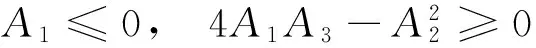
(14)

(15)

(i) 由(7)式知β-a>0,故由(14)式的第一个不等式得

(16)

由韦达定理和A1≤0,只需满足如下不等式就存在μ4>0使上式成立

(17)

(iii) 由(15)式的第一个不等式可得

(18)

注意到B1≤0,μ4>0,从而由上式可看出只要

(19)

第4步：此步主要证明存在s∈[0,1)使(13)式成立即

(20)

注当a=10,b=40,c=1,d=2.5,h=4,Liu系统处于混沌状态[9],易验证(5)-(8)式成立.由(9)式知其混沌吸引子的Lyapunov维数估计为dimLK≤2.512195.

[1]Leonov G A. Lyapunov dimension formulas for Henon and Lorenz attractors[J]. St. Petersburg Mathematical Journal , 2002, 13 (3): 453-464.

[2]Leonov G A. On estimations of the Hausdorff dimension of attractors[J]. Vestnik St.Petersburg University, Mathematics,1991, 24 (3): 41-44.

[3]Leonov G A, Boichenko V A. Lyapunov’s direct method in the estimation of the Hausdorff dimension of attractors[J]. Acta Applicandae Mathematicae ,1992,26 (1):1-60.

[4]Boichenko V A, Leonov G A, Reitmann V. Dimension theory for ordinary differential equations[M]. Teubner, Stuttgart,Journal of Dynamical&Control Systems Press, 2005.

[5]Leonov G A. Lyapunov functions in the attractors dimension theory[J]. Journal of Applied Mathematics and Mechanics, 2012,76 (2): 129-141.

[6]Bhalekar Sachin, Dynamical analysis of fractional order uar prototype Delayed System [J]. Singal Image & Video Processing, 2012, 6(3):513-519.

[7]Oseledec V. Multiplicative ergodic theorem: Characteristic Lyapunov exponents of dynamical systems[J]. Transactions of the Moscow Mathematical Society, 1968,19:179-210.

[8]Hunt B. Maximum local Lyapunov dimension bounds the box dimension of chaotic attractors[J]. Nonlinearity,1996,9(4): 845-852.

[9]陈向荣，刘崇新，王发强，李永勋.分数阶Liu混沌系统及其电路实验的研究与控制[J].物理学报,2008,58(3):1416-1422.

[10]王发强，刘崇新.Liu混沌系统的混沌分析及电路实验的研究[J].物理学报,2006,55(10):5061-5069.

[11]Zhou X, Wu Y, Li Y, Wei Z. Hopf bifurcation analysis of the Liu system[J]. Chaos,Solitons Fractals 2008,36:1385-1391.

[12]Chen H. Chaos control and global synchronization of Liu chaotic systems using linear balanced feedback control[J]. Chaos, Solitons Fractals, 2009,40:466-473.

[13]Xu W, Wang L,Rong H,Li D,Niu Y. Analysis for the stabilization of impulsive control Liu’s system[J]. Chaos, Solitons Fractals ,2009,42:1143-1148.

[14]Kaplan J, Yorke J. Chaotic behavior of multidimensional difference equations, H.-O.Peitgen, H.-O.Walther(Eds), Functional Differential Equations and Approximations of Fixed Points[J]. Lecture Notes in Mathematics, Springer, Berlin, 1979, (730) :228-237.

An Estimation of Lyapunov Dimension of Liu System

HAN Xue-qiong,BAI Xiao-ming

(School of Mathematics, Hefei University of Technology, Hefei 230009, China)

We first obtain an estimation of Lyapunov dimension for invariant sets of Liu system by constructing Lyapunov function based on Lyapunov dimension theory developed by G.A.Leonov, and then we give an estimation of Liu attractors.

dimension theory； Lyapunov function ； Lyapunov dimension ； Liu system

2016-01-18;[修改日期]2016-04-17

安徽省高等学校省级自然科学研究重点项目(2012AJZR0323);中央基本科研业务费(2014HGXJ0076,2014HGXJ0081)

韩雪琼(1992-),女，硕士研究生, 从事生物数学研究.Email:742293028@qq.com

O175.13

A

1672-1454(2016)04-0035-05