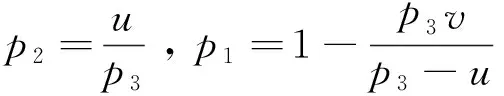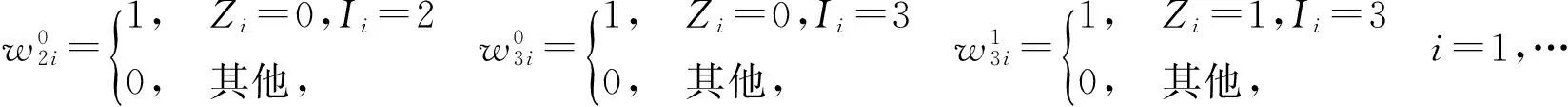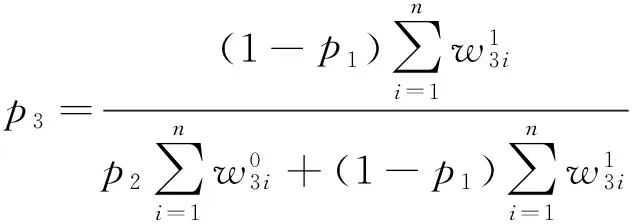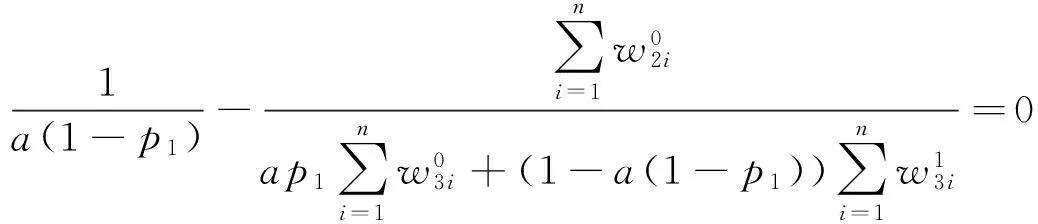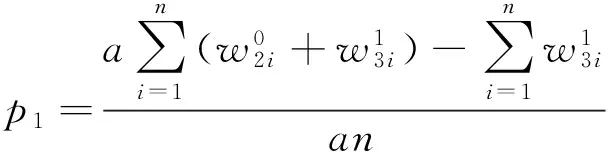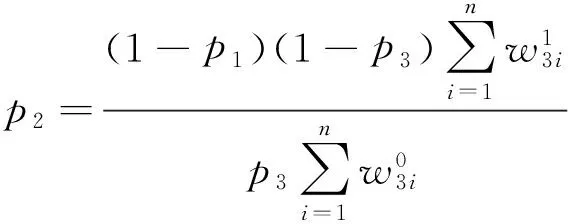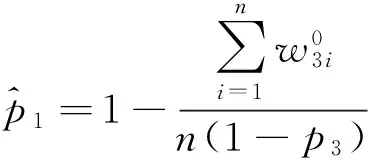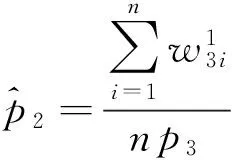例说基于可识最小值之识别性与参数估计及特征的关系
李国安, 李建峰
(宁波大学理学院,浙江宁波315211)
例说基于可识最小值之识别性与参数估计及特征的关系
李国安,李建峰
(宁波大学理学院,浙江宁波315211)
讨论基于可识最小值之识别性与参数估计及特征的关系,以二元Marshall-Olkin型Weibull分布为例,存在全部参数可估计且可识别且有识别特征的情形;以二元McKay型伽马分布为例,存在全部参数可估计且部分参数可识别且无识别特征而有其它分离特征的情形,若是基于可识最小值及差值,则是全部参数可估计且全部参数可识别且有识别特征的情形;以二元极值二点分布为例,存在部分参数可估计且部分参数可识别且有识别特征的情形.
二元Marshall-Olkin型Weibull分布; 二元McKay型伽马分布; 识别性; 参数估计; 特征
1 引 言
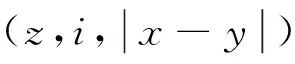
2 全部参数的可识性及可估性及识别特征
记U~WE(α,λ),表示U服从Weibull分布,有密度函数
f(u,α,λ)=αλuα-1e-λxα,u>0.
文献[9]给出了如下的二元Marshall-Olkin型Weibull分布
定义1.1设(X,Y)为二维随机变量,U1,U2,U3为三个相互独立的随机变量,
U1~WE(α,λ1),U2~WE(α,λ2),U3~WE(α,λ3),
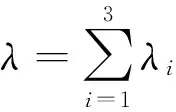
记(X,Y)的联合分布函数为F(x,y),设Z=min(X,Y),设I=1,当Z=X时;I=2,当Z=Y时;I=3,当X=Y时.记P(I=i)=pi,记pifi(z)表示(Z,I)的联合密度,Z的密度函数和分布函数分别记为fZ(·),FZ(·),则有
引理1.1若(X,Y)~MOBW(α,λ1,λ2,λ3),则(Z,I)的分布密度为
证二元Marshall-Olkin型Weibull分布为混合分布,现对其三部分y>x>0,x>y>0,x=y>0分别计算对应的密度.由
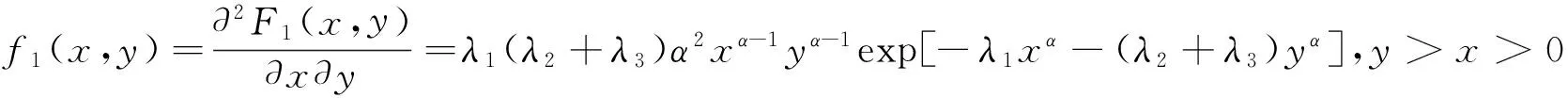
同理
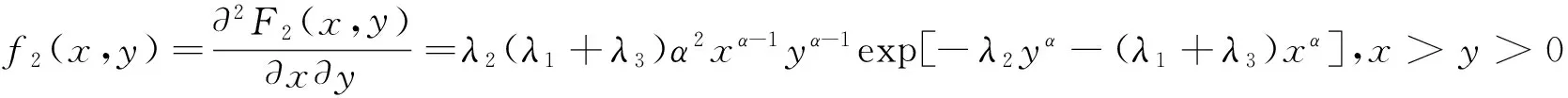

所以
p1f1(z)=λ1αzα-1exp[-(λ1+λ2+λ3)zα],i=1,z≥0,
同理
p2f2(z)=λ2αzα-1exp[-(λ1+λ2+λ3)zα],i=2,z≥0;
由此,连续混合部分的密度为
p3f3(z)=λ3αzα-1exp[-(λ1+λ2+λ3)zα],i=3,z≥0.
显然,λ1,λ2,λ3,α都可识别.
引理1.2若(X,Y)是二元Marshall-Olkin型随机变量,有混合分布F(x,y);则存在相互独立的连续型随机变量Ui,有分布函数Gi(·),(i=1,2,3), 使得X=min(U1,U3), Y=min(U2,U3), 且



引理1.3若(X,Y)是非负的二元Marshall-Olkin型随机变量,有混合分布F(x,y), 则存在相互独立的连续型随机变量Ui,有分布函数Gi(·),(i=1,2,3),使得X=min(U1,U3),Y=min(U2,U3),若给定(Z,I)的联合密度为
则

证由

于是得
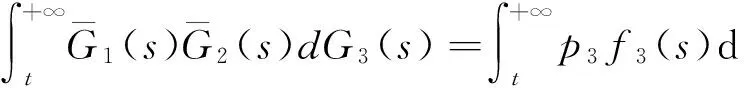
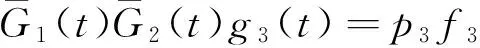
(1)
同理可得

(2)

(3)
由(2)/(3),并移项得
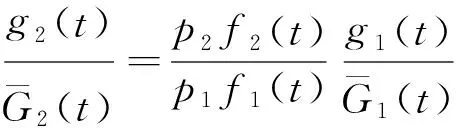
得
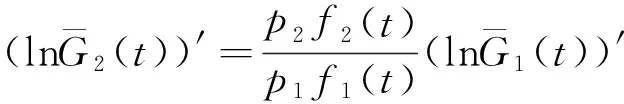

同理可得


则

得
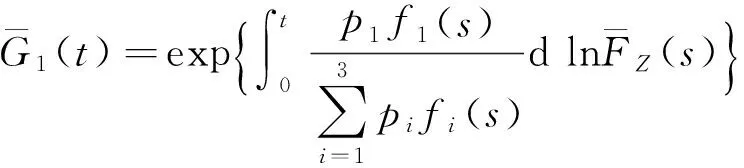
回代上面二式得

因此引理1.3得证.
引理1.4若(X,Y)是非负的二元Marshall-Olkin型随机变量,有混合分布F(x,y),若给定(Z,I)的联合密度pifi(·) (i=1,2,3),则
证综合引理1.2,引理1.3可得.
由引理1.4可得二元Marshall-Olkin型Weibull分布的一个特征.
定理1.1(X,Y)~MOBW(α,λ1,λ2,λ3)当且仅当(X,Y)是二元Marshall-Olkin型随机变量,(Z,I)的联合密度为
定理1.2(X,Y)~MOBW(α,λ1,λ2,λ3)当且仅当(X,Y)是二元Marshall-Olkin型随机变量,Z,I是相互独立的随机变量,且I是一个三值随机变量,Z是一个服从Weibull分布的随机变量.
注二元Marshall-Olkin型Weibull分布的参数估计参见文[9-12],这里略去.
3 部分参数的可识性及全部参数的可估性及分离特征
McKay于文献 [17]中给出了如下的二元伽马分布:
定义2.1称(X,Y)服从二元McKay型伽马分布,其联合密度函数为

记作(X,Y)~BMGD(a,p,q).记Z=min(X,Y),记Z的分布密度为fZ(z),定义随机变量I=1,2分别对应于X 引理2.1若(X,Y)~BMGD(a,p,q),则Z的分布密度为 引理2.2若(X,Y)~BMGD(a,p,q),则(Z,I)的分布密度为 得 定理2.1若(X,Y)~BMGD(a,p,q),(X′,Y′)~BMGD(a′,p′,q′),若已知Z与Z′同分布,则参数a,p是可识别的. 证由fZ(z)=f′Z(z),得 由此得 定理2.2若(X,Y)~BMGD(a,p,q),(X′,Y′)~BMGD(a′,p′,q′),若已知(Z,I)与(Z′,I′)同分布,则参数a,p是可识别的. 证同定理2.1的证明,这里略去. 作变量替换,设Z=X,V=Y-X;则得(Z,V)的联合密度为 于是得分离特征: 定理2.3(X,Y)~BMGD(a,p,q)当且仅当Z=X,V=Y-X相互独立,且Z~GD(a,p),V~GD(a,q),这里Z~GD(a,p)表示Z服从参数为a,p的伽马分布. 证直接由二个联合密度函数相互转换可得. 得方程组 由此得a,p的矩估计分别为 的解. 证由引理2.1和定理2.1,得似然方程 由此得方程组 注1基于(X1,Y1),…,(Xn,Yn),的参数估计问题,形式过于复杂,这里略去. 定义3.1 称(X,Y)服从二元极值型二点分布,是指存在三个相互独立的随机变量U1,U2,U3,其中 U1~B(1,p1),U2~B(1,p2),U3~B(1,p3); 使得 X=max(U1,U3),Y=min(U2,U3),0 记作(X,Y)~BBD(1,p1,p2,p3). 记Z=min(X,Y),定义I=1,2,3分别对应于X 引理3.1若(X,Y)~BBD(1,p1,p2,p3),则Z的分布律为Z~B(1,p2p3). 引理3.2若(X,Y)~BBD(1,p1,p2,p3),则(Z,I)的联合分布律为 定理3.1若(X,Y)~BBD(1,p1,p2,p3), (X′,Y′)~BBD(1,p′1,p′2,p′3),若已知Z与Z′同分布,则所有参数皆不可识别. 定理3.2若(X,Y)~BBD(1,p1,p2,p3),(X′,Y′)~BBD(1,p′1,p′2,p′3),若已知(Z,I)与(Z′,I′)同分布,若其中一个参数已知,则其它参数皆可识. 证由 (1-p3)-(1-p′1)(1-p′3)+p3-p′2p′3=(1-p′3)p′1+p′3(1-p′2), 得恒等式 1-(1-p′1)(1-p′3)-p′2p′3=(1-p′3)p′1+p′3(1-p′2), 记p2p3=u,(1-p1)(1-p3)=v,得 一样可得 若其中一个参数已知,则其它参数皆可识. 定理3.3若(X,Y)~BBD(1,p1,p2,p3)当且仅当(X,Y)是二元极值型随机变量,(Z,I)的联合分布律为 证直接验证可得. 这里,从定理3.2和定理3.3出发,若其中一个参数已知,则可得其它参数的最大似然估计. 定理3.4设(X,Y)~BBD(1,p1,p2,p3)是总体,(X1,Y1),…,(Xn,Yn)是来自总体(X,Y)的容量为n的样本,记Z=min(X,Y),定义随机变量I=1,2,3分别对应于X (Z1,I1),…,(Zn,In)是来自总体(Z,I)的容量为n的样本,若其中一个参数已知,则其它参数的最大似然估计可通过似然方程直接求解可得.这里 证假设三个参数均未知,似然函数为 并有似然方程 得 得 得 得 即三个参数不可能同时可估计.显然,不妨设参数p3已知,得似然方程 得 代入,得 由此得 [1]Basu A P,Ghosh J K.Identifiability of the multinorma and other distributions under competing risks model[J].Journal of Multivariate Analysis,1978,8(3):413-429. [2]李国安.多元 Marshall~Olkin 型指数分布的特征及其参数估计[J].工程数学学报,2005, 22(6):1055-1062. [3]李国安.二元Freund型指数分布的特征及参数估计[J].大学数学,2012,27(5):48-51. [4]Freund, R J. A bivariate extension of the exponential distribution[J] .Journal of American Statistical Association,1961,56:971-977. [5]Marshall A W,Olkin I.A multivariate exponential distribution[J].Journal of American Statistical Association,1967,62(1):30-44. [6]Arnold B C.Parameter rstimation for a multivariate exponential distribution[J].Journal of American Statistical Association,1968,63:848-852. [7]Block H W,Basu A P.A continuous bivariate exponential extension[J].Journal of American Statistical Association,1974,69:1031-1037. [8]Proschan F,Sullo P.Estimating the parameters of a multivariate exponential distribution[J] .Journal of American Statistical Association,1976,71:465-472. [9]Kundu D,Dey A K.Estimating the parameters of the Marshall-Olkin bivariate Weibull distribution by EM algorithm [J]. Computational Statistics and Data Analysis,2009,53:956-965. [10]Li Yang,Sun Jianguo,Song Shuguang.Statistical analysis of bivariate failure time data with Marshall-Olkin Weibull models [J].Computational Statistics and Data Analysis,2012,56:2041-2050. [11]Kundu D,Gupta A K.Bayes estimation for the Marshall-Olkin bivariate Weibull distribution[J].Computational Statistics and Data Analysis,2013,57:271-281. [12]Feizjavadian S H,Hashemi R.Analysis of dependent competing risks in the presence of progressive hybrid censoring using Marshall-Olkin bivariate Weibull distribution[J].Computational Statistics and Data Analysis,2015,82:19-34. [13]Roy D,Mukherjee S P.Characterizations of some bivariate life-distributions[J].Journal of Multivariate Analysis,1989,28(1):1-8. [14]Roy D,Roy R.Characterizations of Bivariate and Multivariate Life Distributions Based on Reciprocal Subtangent[J].Communications in Statistics-Theory and Methods,2009,39(1):158-169. [15]Muliere P,Scarsini M.Characterization of a Marshall-Olkin type class of distributions[J].Annals of the Institute of Statistical Mathematics,1987,39(1):429-441. [16]Kulkarni H V.Characterizations and Modelling of Multivariate Lack of Memory Property[J].Metrika,2006,64(2):167-180. [17]McKay A T.Sampling from batches[J].Journal of the Royal Statistical Society 1 (Suppl.),1934,207-216. [18]Gupta A K,Nadarajah S.Sums, products and ratios for Mckay’s bivariate gamma distribution[J].Mathematical and Computer Modelling,2006,43,185-193. [19]Yue S,Ouarda T B M J,Bobée B.A review of bivariate gamma distributions for hydrological application[J].Journal of Hydrology,2001,246(1):1-18. [20]李国安,李建峰.二元Kundu-Gupta型二点分布参数的最大似然估计[J].大学数学,2015,31(4):113-119. The Relationship Between Identifiability and Parameter Estimation or Characterization Based on Identified Minimum LI Guo-an,LI Jian-feng (Department of Mathematics, Ningbo University, Ningbo Zhejiang 315211, China) The relationship betwreen identifiability and parameter estimation or characterization based on identified minimum is considered in this paper, taking the Marshall-Olkin bivariate Weibull distribution as example,when distribution of identified minimum is known, then all of parameters are identified,this means all of parameters are estimatied, and characterization of the Marshall-Olkin bivariate Weibull distribution based on identified minimum is derived, hence this means distribution of identified minimum is equivalent to its distribution; taking the Mckay’s bivariate gamma distribution as example,when distribution of identified minimum is known, then one of parameters are not identified, and this means one of parameters are not estimatied, and in fact the characterization of Mckay’s bivariate gamma distribution is derived by variate transformation; taking a extreme bivariate Bernoulli distribution as example,when distribution of identified minimum is known, then one of parameters are not identified, and this means one of parameters are not estimatied, and in fact the characterization of a extreme bivariate Bernoulli distribution based on identified minimum is derived. the Marshall-Olkin bivariate Weibull distribution; Mckay’s bivariate gamma distribution; identifiability; parameter estimation; characterization 2016-03-21;[修改日期]2016-05-12 宁波大学学科项目(XKL14D2037) 李国安(1964-),男,硕士,副教授,从事概率统计与土地估价研究.Email:liguoan@nbu.edu.cn. O212.4 A 1672-1454(2016)04-0020-10
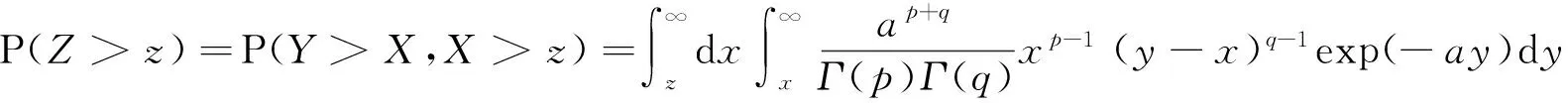


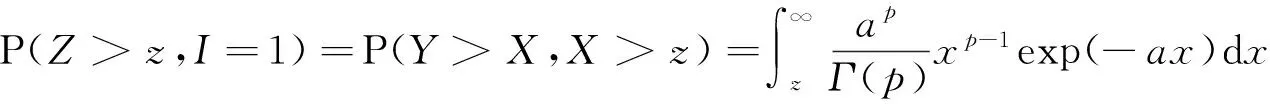


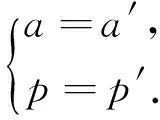
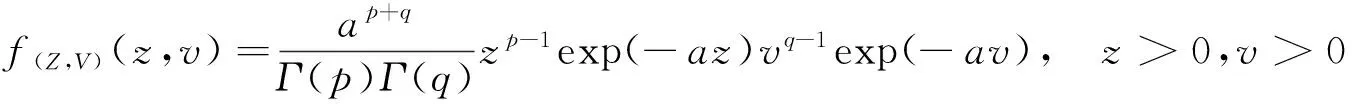
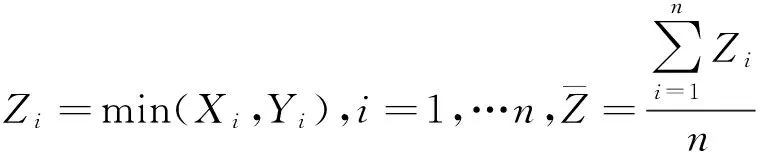
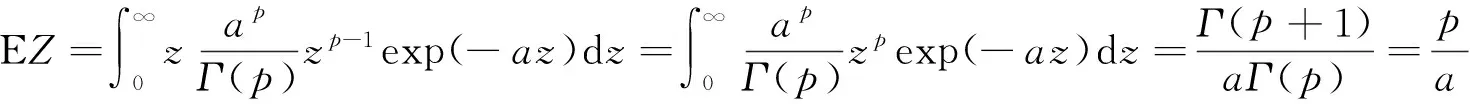

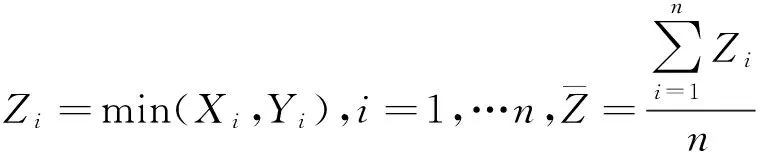
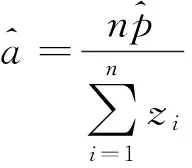
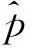
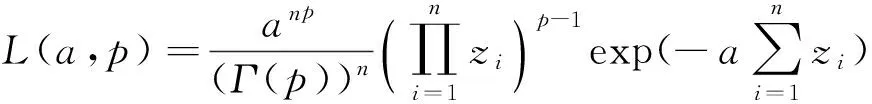

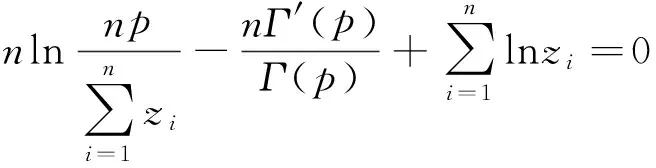
4 部分参数的可识性及部分参数的可估性及识别特征