线性微分方程的一个反问题

高德智

(山东科技大学数学与系统科学学院，山东青岛266590)



线性微分方程的一个反问题

高德智

(山东科技大学数学与系统科学学院，山东青岛266590)

讨论了线性微分方程的一个反问题.给定一个线性无关的函数组，可以得到一个高阶线性微分方程，该微分方程的基本解组恰好是此函数组.另外，对一阶线性微分方程组也进行了类似的讨论.

线性微分方程； 线性无关解； 通解

1　引　　言

微分方程的求解问题是微分方程的核心问题.一般而言，没有通用的方法，但是，对线性微分方程其解的结构我们的认识是比较清楚的.可以先确定对应的齐次方程的通解，再确定一个非齐次的特解，就能把非齐次的通解表示出来.对常系数的高阶线性微分方程和微分方程组，可以通过求特征方程根的方法对相应的齐次方程的基本解组给予完全的刻画.本文中，我们讨论一个反问题：给一个函数组，问在满足什么条件下，它们是某个微分方程的基本解组？该微分方程的具体形式又如何？这类问题只在某些教科书中对一些简单的微分方程讨论过[1,2]，没有一般系统的结论.大多数的研究者主要讨论怎样求解一个微分方程或方程组模型[3,4]，本文中，我们对该问题进行了比较全面的刻画，并通过几个具体的例子说明我们的方法的可行性.我们对反问题的提法略显特殊，对微分方程一般反问题的详尽讨论可参阅专著[5].

2　高阶线性微分方程

定义1函数组y1(x),y2(x),…,yn(x)称为在区间I上是线性相关的，如果存在一组不全为零的常数λ1,λ2,…,λn，使得

λ1y1(x)+λ2y2(x)+…+λnyn(x)=0

在I上恒成立.否则称y1(x),y2(x),…,yn(x)在区间I上是线性无关的.

定义2设函数组y1(x),y2(x),…,yn(x)在区间I上有直到n-1阶的连续导数，称行列式

为函数组y1(x),y2(x),…,yn(x)在区间I上的朗斯基行列式.

对一般的n阶线性齐次微分方程

y(n)+a1(x)y(n-1)+…+an-1(x)y′+an(x)y=0

(1)

有下面的定理：

定理1设函数组y1(x),y2(x),…,yn(x)是方程(1)在区间I上的n个解，则

(i) 此n个解在I上线性相关的充分必要条件是在I上W(x)≡0；

(ii) 此n个解在I上线性无关的充分必要条件是∀x∈I，有W(x)≠0.

下面考虑一个相反的问题，给定一个在某区间I上n个线性无关的函数组y1(x),y2(x),…,yn(x)，问在满足什么条件下它们是某个n阶线性微分方程的一组基础解.

定理2设函数组y1(x),y2(x),…,yn(x)在区间I上有直到n阶的连续导函数，且其朗斯基行列式W(x)≠0，则一定存在一个n阶线性微分方程，使得它的基础解恰为

y1(x),y2(x),…,yn(x).

证由于∀x∈I，有W(x)≠0，则行列式

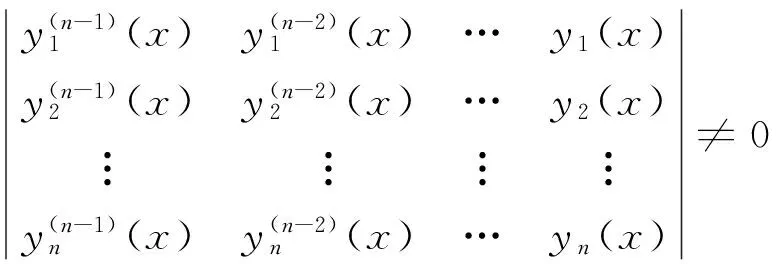
这样，方程组

必存在唯一解a1(x),a2(x),…,an(x)，且在区间I上连续.则微分方程

y(n)+a1(x)y(n-1)+…+an-1(x)y′+an(x)y=0

就是要求得方程.

例1当λ1≠λ2时，y1=eλ1x,y2=eλ2x是两个线性无关的函数，求解微分方程

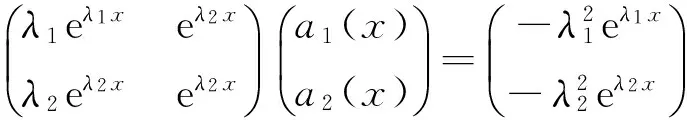
容易得到

a1(x)=-(λ1+λ2),a2(x)=λ1λ2.

所得微分方程为

y″-(λ1+λ2)y′+λ1λ2y=0.

该结论和我们正面求解微分方程时，所得到的结论是一致的.

例2取y1=ex,y2=cosx，利用上述方法可以求得对应的微分方程为

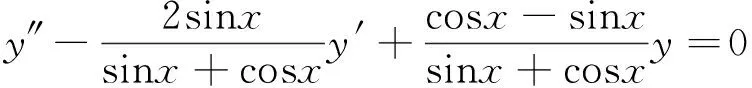
这个例子，要是正面求解将非常困难.

3　一阶线性微分方程组

对于一阶线性微分方程组，也可以得到类似的结论.

定理3设

是n个向量函数，在区间I上每个分量函数有连续的导函数，且在区间I上行列式

(2)

则一定存在唯一的一组连续函数aij(x),i,j=1,2,…,n，使得yi(x)是微分方程组

证∀x∈I，作下面的代数方程组

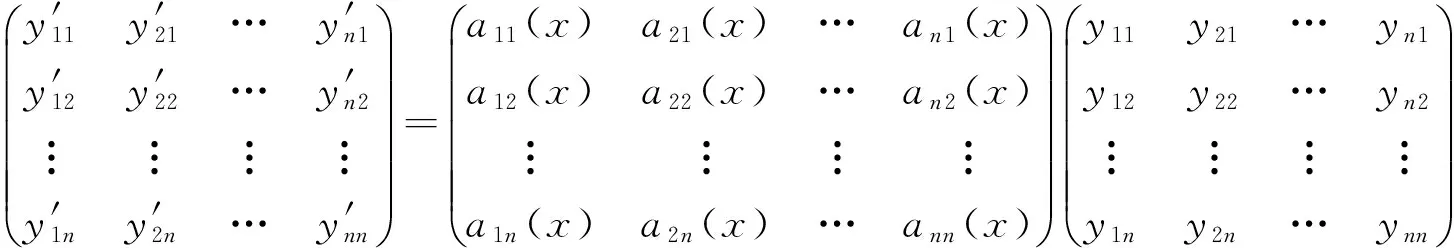
(3)

由条件(2)知，方程组(3)存在唯一的一列函数aij(x),i,j=1,2,…,n满足该方程组.由此得到函数组yi(x)是微分方程组

的解，又因为是该函数组是线性无关的，所以它们的通解为

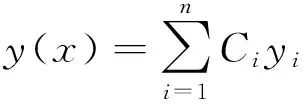
例3取函数组为

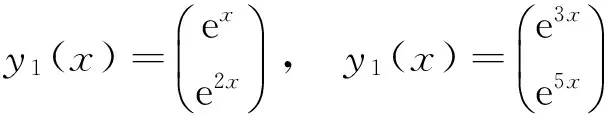
按照上面的方法，只需求下面的方程组

即可.经过简单的计算

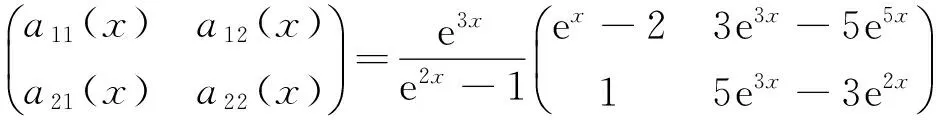
由此得到所求的微分方程组为

我们在上面讨论了一个微分方程的反问题，该问题提供了一个在已知一组函数组的情形下求微分方程或方程组的一般方法，在实际应用中还是很有意义的.另外，通过该反问题的讨论也使学生进一步理解微分方程解的唯一性问题和求解问题.当我们间接知道一个系统的一组线性无关的解时，可以通过上述方法反求出该系统满足的微分方程或方程组，从而更清楚地研究该系统的其他相关问题.因此，我们所讨论的问题在理论上还是很有意义的.

[1]伍卓群，李勇.常微分方程[M]. 北京：高等教育出版社，2004.

[2]袁荣.常微分方程[M].北京：高等教育出版社，2012.

[3]彭庆英.常系数线性微分方程组的基解矩阵的新求法[J]. 《大学数学》，2013,29(6)：120-124.

[4]金路，朱大训.一阶线性微分方程的一种解法[J].《大学数学》，2013,29(2)：86-90.

[5]Romanov V G,Vasiliev A M.Multidimensional inverse problems for differential equations[M]. Berlin: Springer-Verlag, 1970.

An Inverse Problem of Linear Differential Equations

GAO De-zhi

(College of Mathematics and Systems Science , Shandong University of Science and Technology,Qingdao Shandong 266510,China)

An inverse problem of linear differential equations is considered in this paper. Given a group of independent functions, a high-order linear differential equation can be obtained, whose foundational solutions are just the given functions. In addition, the similar problem is also discussed for the first order linear differential systems.

linear differential equation; linearly independent solutions; general solution

2014-12-30；[修改日期]2016-05-08

国家自然科学基金(11271007)

高德智(1963-),男，博士，教授，主要从事应用泛函分析方面的教学与研究工作.Email:gaodezhi@sdust.edu.cn

O175.1

C

1672-1454(2016)04-0078-04