曲线积分的换元法

宁荣健，　彭凯军

(合肥工业大学数学学院，合肥230009)



曲线积分的换元法

宁荣健，彭凯军

(合肥工业大学数学学院，合肥230009)

给出了曲线积分的换元法，丰富了曲线积分的计算方法.

曲线积分； 换元法； 平面曲线； 空间曲线； 变换

1　问题的提出

在数学分析和高等数学课程的教学过程中，分别介绍了定积分的换元法和重积分的换元法，那么曲线积分是否有换元呢？理论上说应该是可以肯定的，但是具体涉及到两类曲线积分，其换元法分别是什么？下面我们来具体讨论.

2　主要结论

定理1(对弧长的平面曲线积分换元法)设平面曲线L的方程为φ(x,y)=0，变换

将uOv平面上的平面曲线L′一对一地变为xOy平面上的L，其中φ(x,y)在L上具有一阶连续偏导数，x(u,v),y(u,v)在L′上具有一阶连续偏导数，且

f(x,y)在L上连续.则

解法一将曲线L的方程转化为(x-2y)2+y2=1.令x-2y=cost,y=sint,得L的参数方程为

故

令φ(x,y)=x2-4xy+5y2-1，故φ′1=2x-4y,φ′2=-4x+10y，所以

且L′:u2+v2=1，故利用定理1得

I=∫L′dsuv=L′的弧长=2π.

推论1在定理1中，如果J为正交矩阵，则

∫Lf(x,y)ds=∫L′f(x(u,v),y(u,v))dsuv.

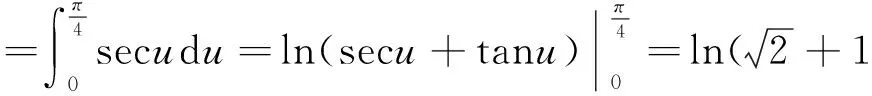
与定理1相仿，有

定理2(对弧长的空间曲线积分换元法)设空间曲线Γ的方程为

变换

将O-uvw空间中的曲线Γ′一对一地变为O-xyz空间中的Γ，其中φ(x,y,z)，ψ(x,y,z)在Γ上具有一阶连续偏导数，x(u,v,w),y(u,v,w),z(u,v,w)在Γ′上具有一阶连续偏导数，记G(x,y,z)=gradφ(x,y,z)×gradψ(x,y,z),如果

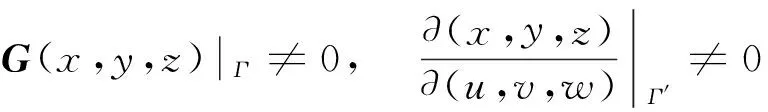
f(x,y,z)在Γ上连续.则

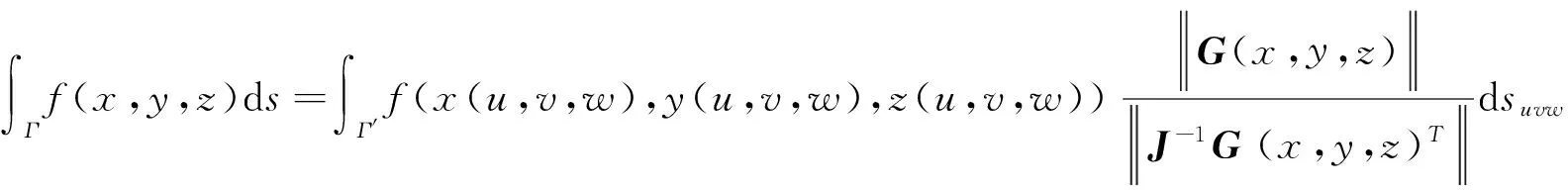
其中

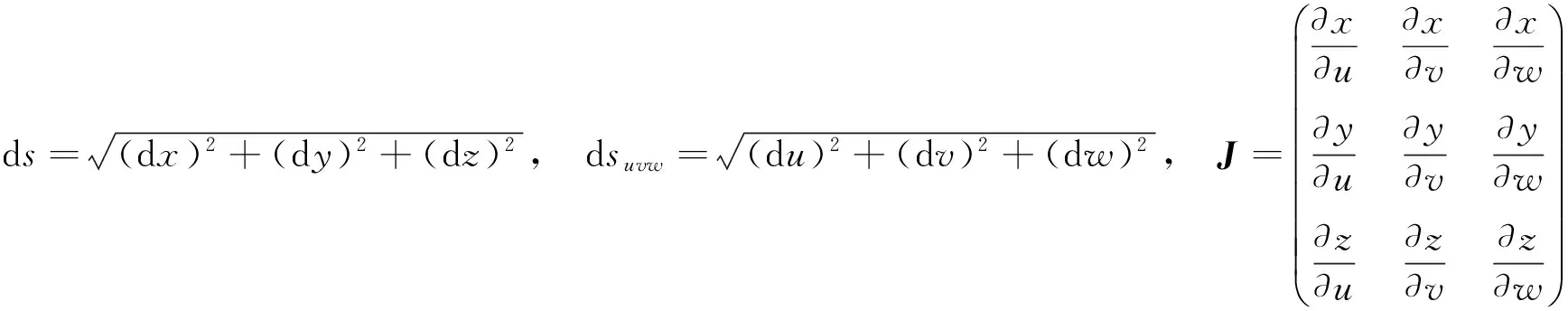
推论2在定理2中，如果J为正交矩阵，则

∫Γf(x,y,z)ds=∫Γ′f(x(u,v,w),y(u,v,w),z(u,v,w))dsuvw.

下面给出对坐标的曲线积分换元法.

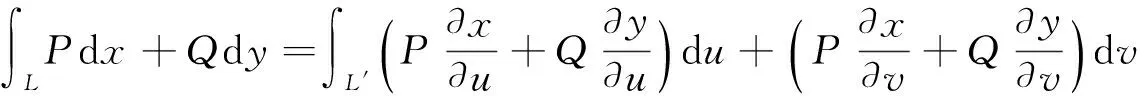
定理4(对坐标的空间曲线积分换元法)设Γ为空间有向光滑曲线，起点为A，终点为B.变换

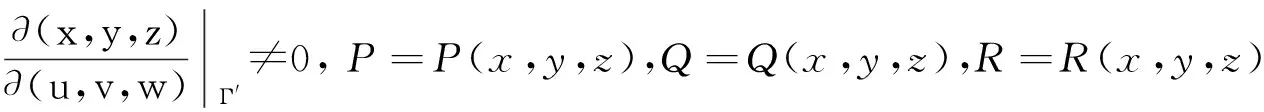
∫ΓPdx+Qdy+Rdz

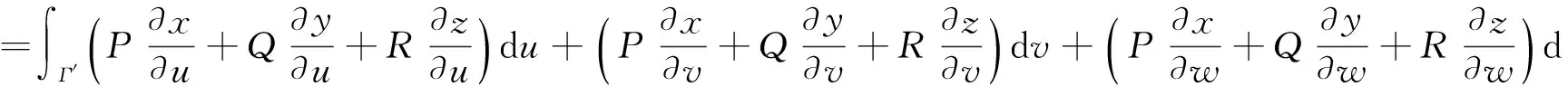
注在定理3中，如果L为有向封闭曲线，则在L上任取三点A,B和C，将L分为三个有向线段L1,L2和L3，其中L1的起点为A，终点为B；L2的起点为B，终点为C，L3的起点为C，终点为A.在变换

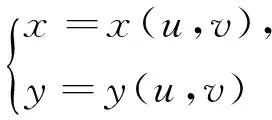
下，L变为L′，A,B,C分别变为A′,B′,C′，L1,L2,L3分别变为L′1,L′2,L′3，其中L′1的起点为A′，终点为B′；L′2的起点为B′，终点为C′，L′3的起点为C′，终点为A′，并由此确定L′的方向.

在定理4中，如果Γ为有向封闭曲线，则可运用同样的方法确定L′的方向.

若从z轴正向向原点看去，Γ为逆时针方向.

又Σ在xOy平面上的投影区域为椭圆区域Dxy:2x2+2y2+2xy-2x-2y≤0.作正交变换

解法二采用变换思想，利用定理4计算此积分.

由于空间曲线Γ位于平面x+y+z=1上，因此通过变换将平面x+y+z=1变换为O-uvw空间中的平行于uOv坐标面的平面.因为x+y+z=1的法向量为{1,1,1}，由此构造正交向量组{1,-1,0}，{1,1,-2}，{1,1,1}，再单位化后得

故作正交变换

3　小　　结

曲线积分的换元法进一步完善了曲线积分的理论，丰富了曲线积分的计算方法.尤其是当平面曲线为二次曲线，且其方程不是标准型时，可通过变换将其转化为标准型后，运用定理1或定理3简化曲线积分计算.当空间曲线为柱面(母线未必平行于坐标轴)、旋转曲面(对称轴未必平行于坐标轴)、二次曲面(其方程未必为标准型)与平面(未必平行于坐标面)的交线时，可通过变换将其转化为平行于坐标面的平面曲线，且其方程为标准型后，运用定理2或定理4计算曲线积分.

需要指明的是，在运用对坐标的曲线积分换元法时，确定变换后曲线的方向是一件非常重要，也具有一定难度的事情.

对于曲面积分的换元法，我们另有讨论.

[1]朱士信、唐烁、宁荣健、任蓓、郑靖波，高等数学(下)[M].北京：高等教育出版社，2015:175-188.

A Substitution Method of Curve Integral

NING Rong-jian ,PENG Kai-jun2

(School of Mathematics, Hefei University of Technology, Hefei 230009, China)

A substitution method of curve Integral is presented, the method enrich the calculation method of curve integral.

curvilinear integral; substitution method; plane curve; space curve; transformation

2016-05-11；[修改日期]2016-06-12

安徽省重大教学改革项目(2015zdjy020)；受“高等学校大学数学教学研究与发展中心”资助

宁荣健(1962-)，男，副教授，从事计算数学研究和大学数学教学，Email:nrjian@126.com

彭凯军(1979-)，男，讲师，从事计算数学研究，Email:lxy_pkj@126.com

O13； O172.2

C

1672-1454(2016)04-0062-06