轧机板形控制域的计算及其实践应用①

智西巍，陈孝明，李山青

(宝山钢铁股份有限公司，上海　201900)



轧机板形控制域的计算及其实践应用①

智西巍，陈孝明，李山青

(宝山钢铁股份有限公司，上海201900)

基于分段离散法研究了轧机板形控制域的具体计算步骤及方法，并使用该计算方法对某新建轧机的板形控制域进行了计算，通过与目标板形控制域相比较，最终确定了该轧机弯辊力范围与轧辊横移量范围的设计参数。

板材轧机； 辊缝； 辊凸度； 板形控制

引　言

板带材产品有四大质量指标：板形精度、厚度精度、表面质量、力学性能，其中板形精度一般是指板带材的平直度，是板带材的主要外观体现。随着科学技术的进步及市场竞争的激烈化，不但用户对板形精度提出了更高的要求，作为钢铁生产企业，也将板形控制能力视为轧制关键技术[1]。持续提高并掌握板形控制能力成为了钢铁生产企业一致追求的目标。为使得带钢保持平直性，必须控制辊缝形状，使得带钢在轧制前后保持等比例凸度[2]。

一般可以根据板带横截面的几何形状，将其凸度分解为常数部分、一次部分、二次部分和高次部分[3]。对于常数部分和一次凸度部分，一般都较容易控制，因此轧机的板形控制能力主要体现在轧机对辊缝形状曲线二次凸度和高次凸度的控制能力。在二维图形上，以辊缝形状曲线的二次凸度作为纵坐标，高次凸度作为横坐标，将轧机在不同板形调控手段下所能达到的二次凸度及高次凸度值在图中标出，将这些点围成的区域称为板形控制域，又称辊缝形状调控域、辊缝凸度调节域。该区域越大，说明该种轧机对二次和高次凸度的控制能力越强，即对板形的控制能力也越强。

通过分析轧机的板形控制域，可以量化地分析、评价轧机的板形控制能力，为轧机的轧制工艺优化，特别是为轧机参数设计及技术改造时提供依据。因此，研究如何通过理论计算来分析、评价轧机的板形调控能力，具有非常重要的实际应用意义。

1　计算方法

对轧辊辊缝形状的计算，实际上是对轧辊弹性变形的计算，其计算方法主要有解析法[4]、分段离散法[5]、有限元法[6]等。其中分段离散法(或称影响函数法、分割法、条元法)是一种离散化方法，其基本思想是：将轧辊及辊间的接触压力离散为有限个单元，基于数学物理方程中的影响函数的概念，确定各单元对辊身其他位置的影响，然后将各自的影响相互叠加，得到各单元的变形量，从而确定板带的厚度分布[7]。下面以六辊轧机为例，介绍其计算方法及步骤。

1.1辊形弹性变形计算

将轧件作用给工作辊的载荷沿轧制中心线向两侧各分成M段并用集中力Q′来表示，支承辊与中间辊辊间压力分成N段并用集中力Qmb来表示，中间辊与工作辊辊间压力分成N1段并用集中力Qmw来表示，其他各参数如图1所示。

根据各轧辊的受力情况，可以计算出各轧辊的挠度，以工作辊为例，其挠度可用以下公式来描述

(1)

图1　六辊轧机辊系弹性变形分析模型

式中yw为工作辊挠度；Qmw，Q′为工作辊与中间辊、轧件与工作辊间单位长度接触压力；GwL，GwR为工作辊相对轧制中心线左右两侧的弯曲影响系数；FwL，FwR为工作辊左右侧弯曲力；GFwL，GFwR为工作辊左右侧弯曲力影响系数；θw为工作辊相对支承辊的转角；X为距离轧制中心线的距离。

根据所得到的各轧辊挠度公式，假定轧辊之间完全为弹性变形，则可以列出轧辊接触区的变形协调方程，以工作辊与中间辊之间的接触区为例，其变形协调方程为

(2)

其中

(3)

式中ymw为辊间压扁变形；Crw(i)，Crm(i)为工作辊、中间辊初始凸度；vw，vm为工作辊、中间辊泊松比；Dw，Db为工作辊、中间辊直径；Ew，Eb为工作辊、中间辊弹性模量；Qmw为工作辊、中间辊辊间单位长度接触压力；b为接触宽度。

辊系平衡方程主要是指力平衡方程和力矩平衡方程，包括各轧辊的力平衡方程和力矩平衡方程，以工作辊为例，可以列出以下公式：

(4)

(5)

同理，可以列出中间辊、支撑辊的力平衡和力矩平衡方程，得到辊系的力平衡和力矩平衡方程。

联立以上方程并求解，最终可以计算出工作辊在弹性变形后的辊缝曲线。

1.2辊缝二次凸度和高次凸度计算

通常假定带钢是相对于轧制中心线左右对称的，因此，承载的辊缝凸度可以用一个最高阶次为四次的偶函数多项式来近似地描述[8]，其中常数部分可以略去

(6)

式中f(X)为承载辊缝凸度；f2(X)，f4(X)为承载辊缝二次凸度及四次凸度；a1，a2为—拟合曲线2阶、4阶系数；X为正则化处理后的沿带钢宽度上的坐标(-1 ≤X≤1)。

以轧制中心线f(0)和带钢两侧边缘f(1),f(-1)为三个特征点提取二次多项式，将其视为二次凸度函数，将其他部分视为四次凸度函数，即

(7)

用其极值减去边部值，即可得到承载辊缝的二次、四次凸度值，分别为

(8)

2　计算应用与结果

某新建六辊轧机的轧辊主要参数如表1所示，设计要求该轧机二次凸度的控制能力在其轧制宽度范围内(700～1300 mm)均能超过±50 μm。

表1　轧辊主要参数

为此，根据上述的计算方法，基于Fortran语言编制了板形控制域计算程序，初步确定的工作辊弯辊力范围为-180～360 kN，中间辊弯辊力范围为0～500 kN，中间辊窜辊量定义为20～320 mm。分别在不同轧制力(5，10，15 kN/mm)和不同带钢宽度(700，1000，1300 mm)下，计算了工作辊与中间辊弯辊力处于上下限情况下的辊缝凸度，绘制成板形控制域，结果如图2 ～ 4所示。

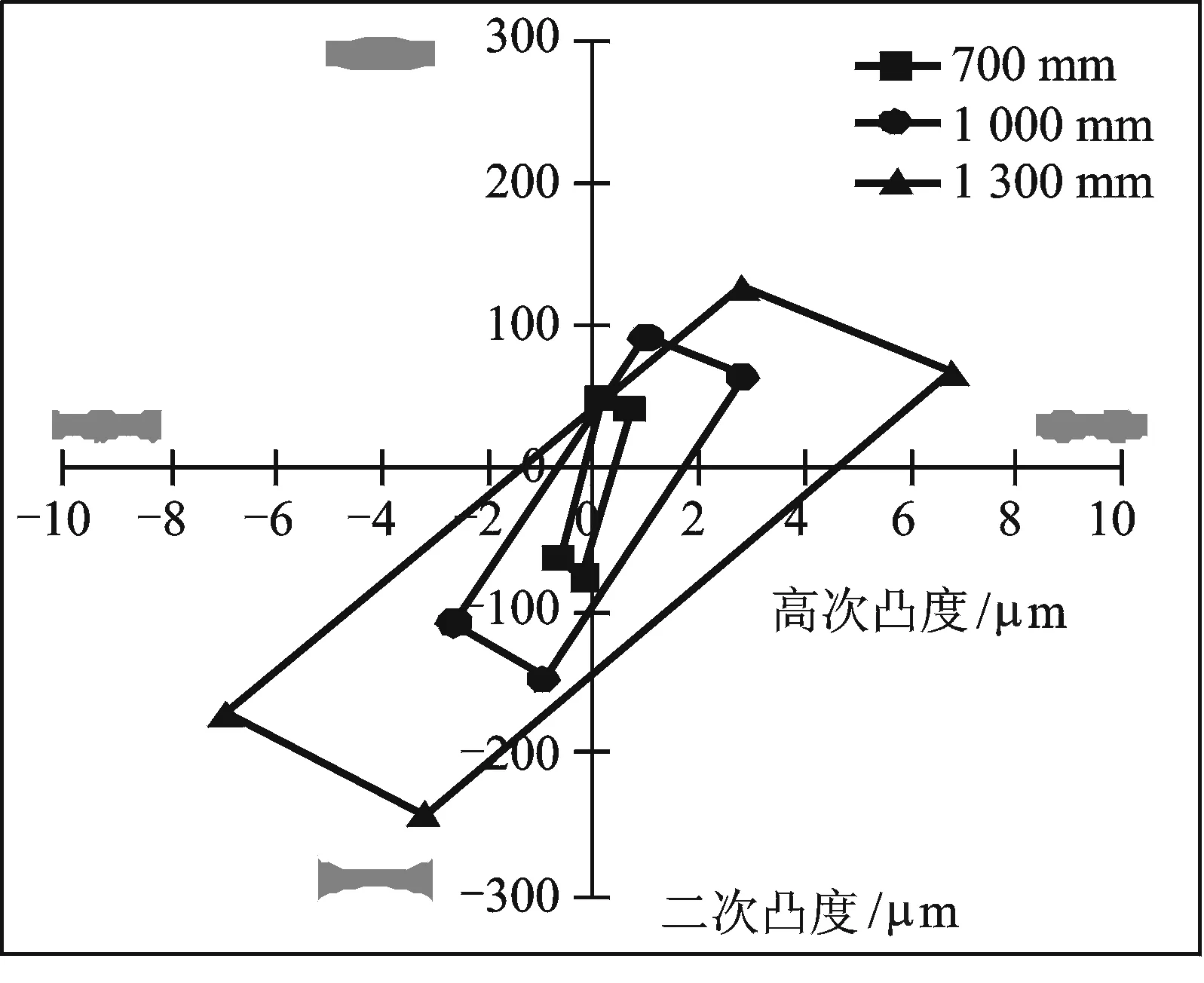
图2　轧制力为5 kN/mm时不同带钢宽度的板形控制域

图3　轧制力为10 kN/mm时不同带钢宽度的板形控制域

图4　轧制力为15 kN/mm时不同带钢宽度的板形控制域

由计算结果可知，在所确定的设计参数下，即使在最小的带钢宽度(700 mm)时，二次凸度的控制能力均超过±50 μm，同时对高次凸度也具备一定的控制能力，符合设计要求。但考虑到轧辊倒角、后续规格扩展等因素，最终确定的工艺参数为：工作辊弯辊力范围为-180～360 kN，中间辊弯辊力范围0～500 kN，窜辊量范围为0～380 mm。

采用以上参数设计的轧机，在实际生产中可以长期稳定地批量轧制包括厚度0.18 mm特薄板在内的各种产品，全部规格板形精度≤6I达96%以上，充分证明了设计参数选取的合理性。

3　结束语

应用分段离散法，编写计算程序计算某新建六辊轧机的板形控制域的各项参数，根据计算结果确定了该轧机的弯辊力、窜辊量参数，经现场实际使用验证，结果表明：理论计算结果与现场实际应用效果相符。相关研究结果可以为其他轧机的设计选型、技术改造提供指导。

[1]李坤. 板形控制的发展及其应用[J]. 硅谷. 2011，(06):140.

[2]左远鸿. 热轧带钢断面轮廓的控制与优化[J]. 中国冶金. 2013, 23(7):37-39.

[3]令狐克志, 宋浩源, 王永强,等. 六辊CVC冷轧机凸度控制能力分析及应用[J]. 钢铁, 2014，49(11)：53-58.

[4]戴杰涛, 张清东. 冷轧薄板中浪板形缺陷的屈曲及后屈曲理论与轧试验研究[J]. 机械工程学报. 2011, 47(2):44-50.

[5]张立昌, 刘佳冰. 四辊轧机辊系变形的影响函数法[J]. 一重技术. 2008,(06):4-6.

[6]Sun J, Du F, Li X. FEM Simulation of the Roll Deformation of Six-high CVC Mill in Cold Strip Rolling[A], 2008 International Workshop on Modeling, Simulation and Optimization[C]. New York: IEEE Computer Society, 2009:412-415.

[7]麻永林, 宫美娜, 邢淑清,等. 304不锈钢带板形控制的有限元分析[J]. 钢铁. 2015,(2):48-53.

[8]李勇华. 冷轧薄带板形控制技术研究[D]. 沈阳：东北大学, 2010.

2016-05-06

智西巍(1960—)，男，硕士，高级工程师。E-mail：zhixiwei@baosteel.com

TG333.7