专题聚焦，经营开放，注重反馈——以“点到‘线’的距离专题复习课”为例

☉江苏省泰州市姜堰区实验初级中学于真良

专题聚焦，经营开放，注重反馈
——以“点到‘线’的距离专题复习课”为例

☉江苏省泰州市姜堰区实验初级中学于真良

中考复习的教学实践中，常常碰到一些“超越”初中教材上的习题要求，比如，平面直角坐标系内的点到“线”（直线、抛物线等）的距离，就是一类较难问题，虽然在中考中不宜直接考查点到抛物线的距离问题，但是复习资料或平时有些模考中这些习题还是客观存在的，如何跟初中生讲评这类问题，确实值得思考.本文就是基于上述认识，构思的一节习题课，提供研讨.

一、“点到‘线’的距离”习题教学流程

教学环节一：从平面几何中的“距离”说起

问题1：同学们在初中几何学习中，学到了哪几种“距离”？

预设：点到点之间的距离、点到直线的距离、平行线之间的距离.并安排学生上台画图演示，复习几种距离的概念.并指出，点到直线的距离是所谓垂线段的长，本质上也是转化为点到垂足之间的距离，最终还是化归为点到点的距离.类似的，平行线之间的距离也是化归为两点之间的距离.

教学环节二：变式研究“两点之间的距离”

问题2：如图1，数轴上的点A、B分别对应着数1、3，则线段AB的长为多少？

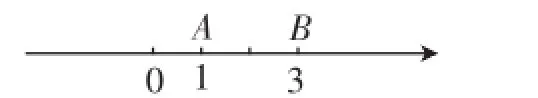
图1

问题3：若数轴上点A、B分别对应着数a、b，则线段AB的长为多少？（用含a、b的式子表示）

问题4：平面直角坐标系中，点C在y轴上，且到原点的距离为3，则点C的坐标是？

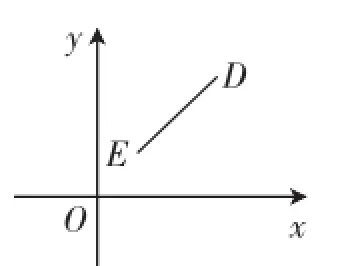
图2

问题5：如图2，在平面直角坐标系中，点D（3，3），E（1，1），分别求出点D、E到x轴的距离，以及线段DE的长.

问题6：在“问题5”的条件下，分别求出点D、E到原点的距离.

设计意图：通过上述问题，引导学生思考在平面直角坐标系中点与点之间距离的各种可能有的求值方向，追求“做一题、会一类、通一片”的教学效果.特别是对于“问题5”，引导学生归纳出两点之间距离公式：若A（x1， y1），B（x2，y2），则

教学环节三：变式研究“点到直线的距离”

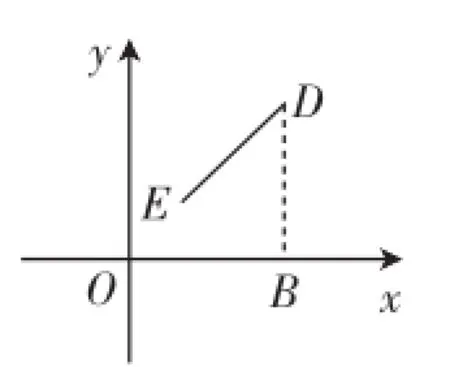
图3

问题7：如图3，在平面直角坐标系中，点B（3，0），D（3，3），E（1，1），求点B到直线DE的距离.

预设：如果学生没有思路，则启发他们过点B作出DE的垂线段，并思考如何求该垂线段的长，这时如果从几何角度发现DE所在直线即为y=x，对于贯通思路是关键的，可以通过启发或追问，促进学生自主思考出来.比如，设计启发式问题“能否求出直线DE的解析式？”“直线DE有什么特殊呢？”

问题8：如图3，在平面直角坐标系中，点B（3，0），D（3，3），E（1，1）.若P为线段DE上任意一点，连接BP，当PB取得最小值时，求点P的坐标.

设计意图：学生可以在上一问的基础上，进一步思考求出点P的坐标；在此基础上，注意启发学生从点到点的距离公式分析，预设如下：

由直线DE的解析式为y=x，则可设P（m，m），于是PB=即当m=1.5时，PB获得最小值，此时P（1.5，1.5）.

学生通过上述运算的方法体会不同解法之间的殊途同归.

问题9：平面直角坐标系中，点C（0，3），直线l：y=x-3上有一点P，连接CP，当CP取得最小值时，求出点P的坐标，以及此时PC的长.

设计意图：有了“问题8”的殊途同归的“数”、“形”的不同方法，学生可以从图形直观的视角洞察出很多等腰直角三角形，从而发现待求的点P即为直线y=x-3与x轴的交点（3，0），PC获得最小值3；也可以从两点之间距离公式来分析，预设如下：

因为直线的解析式为y=x-3，则可设P（m，m-3），于是，即当m=3时，PC获得最小值3√2，此时P（3，0）.

教学环节四：拓展思考“点到抛物线上任意一点的距离最小值”

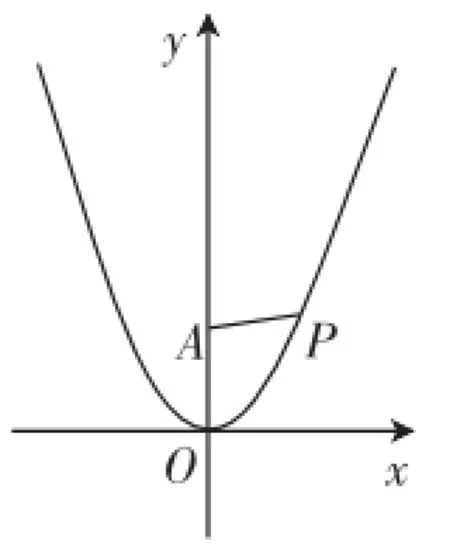
图4

问题10：如图4，在平面直角坐标系中，点P为抛物线y=x2上任意一点，点A（0，2），连接AP，试分析AP的最小值.

预设：这时学生认为用直观解法可能不太方便，需要走“数”的角度精确运算，比如，运用两点之间距离公式，因为抛物线的解析式为y=x2，则可设P（m，m2），于是AP=时，AP获得最小值

问题11：如图5，在平面直角坐标系中，点P为抛物线y=x2上任意一点，点A（0，2），以P为圆心，半径为1作圆，在⊙A上取一点Q，连接PQ，试分析PQ的最小值.

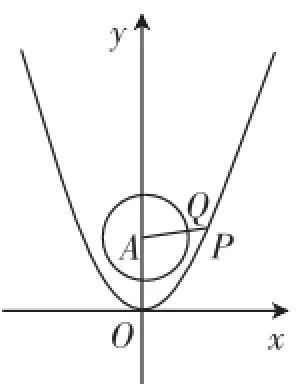
图5

设计意图：这是“问题10”的变式问题，本质上仍然是AP取得最小值时，PQ也获得最小值，因为AQ是定值1.事实上，这类问题还可以有进一步的包装，在不少地区的模考卷中也曾有见到，比如，过点P作⊙A的切线，设切点为M，当切线PM取得最小值时，求点P的坐标.

教学环节五：课堂小结与当堂检测

小结问题：点到点的距离、点到线的距离虽然是一个小话题，然而展开、深入探究之后，我们发现，这只是开了一个头，特别是点到“曲线”的距离的研究之门，才刚刚打开，以后同学们在高中阶段还会有深入的学习和研究.

听课检测题：（5个小题，每小题20分）

在平面直角坐标系xOy中，点A（2，0），B（3，0），C（0，4），D（2，4）.

（1）直接写出点A、C之间的距离；

（2）求直线BC的解析式；

（3）求原点O到直线BC的距离；

（4）求点D到直线BC的距离；

（5）若经过点D的抛物线y=ax2上有一点P，连接PC，请分析PC的最小值.

二、教学立意的进一步阐释

1.聚焦专题复习，通过系列变式促进学生深入思考

中考复习遇题讲题，零乱散击效果并不如意，或者是模考后就题讲题，这样的收获也是零散的.当学生遇到一类前所未见的题型或方法时，如果能开发成专题复习，通过系列变式促进深入思考相关话题，既可以把一类陌生问题达到深刻理解，也可以通过系列变式促进学生深入思考.特别是，我们在课例初始问题中提出的一系列问题（问题1～问题11），这些都是课前精心预设的.

2.经营开放教学，通过拓展追问促进学生向上挑战

郑毓信教授倡导的开放的数学教学，要求我们从开放题走向开放的数学教学.我们正是想在一个主要题干下，通过系列问题或深入追问引导学生参与思考，把学生的思维卷入课堂问题，并鼓励优秀学生向上挑战，甚至把思考引向课后，追求“课堂时间有尽，思考却可以延续到课外”的学习取向.

2.注重跟进反馈，通过同类变式及时反馈听课效果

根据教学实践，加强听课检测的反馈是小专题复习课的必要环节之一，因为不少学生常常是课上听懂了，却不能独立求解.所以我们在课堂小结之后安排了限时检测的环节，并设计了与课常上所学习内容结构相同的变式习题，只是变换了数据而已，如果学生真正理解问题的结构，则只是再次运算、求解一遍.可以有效地检测反馈听课效果.

三、结束语

中考复习是一个老生常谈的话题，如何系统复习？如何老歌新唱、唱出新意？如何引导学生以小见大、小中想深、想向远方？这些都是笔者近来复习期间的思考所及，困惑也多于此，故愿意写出来，抛砖引玉，期待同行们的实践跟进与批评指正.

1.罗增儒.数学解题学引论［M］.西安：陕西师范大学出版社，2008.

2.【美】波利亚，著.怎样解题［M］.阎育苏，译.北京：科学出版社，1982.

3.钟启泉.“批判性思维”及其教学［J］.全球教育展望，2002（1）.

4.刘东升.经历问题生成，深刻理解教材——人教八上“每日一题”的命题实践与思考［J］.中学数学（下），2014（4）.H