复习课要有“复习味”——以“一元二次方程根的判别式”复习为例

☉江苏省苏州市高新区第一中学李莎莉

复习课要有“复习味”
——以“一元二次方程根的判别式”复习为例

☉江苏省苏州市高新区第一中学李莎莉

根据教学内容的不同，我们常将数学课分为新授课、复习课、试卷讲评课和练习课.初中阶段，复习课是仅次于新授课的一种课型，到了初三下学期，复习课更是成为了“主打”课型.为帮助学生获取中考的最大利益，中考前夕，几乎所有的学校都会安排较长的时间集中复习.在这一阶段，复习课的主要任务就是帮助学生将已经遗忘的知识唤醒，培养他们应用数学知识分析问题与解决问题的能力.显然，复习课主要是重复“学生学过的知识”，加深学生对这些知识的印象，使其在脑海中留存更长的时间.然而，在近期的一次随堂听课中，一位老师将“一元二次方程根的判别式”复习课上出了浓浓的“新授味”，偏离了复习的主旨，耗时不少，复习成效却并不好.现结合这节课的“前半段”及对此的优化谈谈笔者的感悟，希望能给你带来一些启示.

一、教学片断及简析

1.教学片断

投影三个方程如下：

（1）2x2-3x=0；

（2）3x2-2x+1=0；

（3）4x2+x+1=0.

教师：这三个方程有什么共同特征？

学生（齐）：都是一元二次方程.

教师：对！一元二次方程的一般形式是什么？

学生1：ax2+bx+c=0（a≠0）.

教师：你能说出这三个方程中a、b、c的取值分别是多少吗？

学生2：方程（1）中，a=2，b=-3，c=0.

学生3：方程（2）中，a=3，b=-2，c=1.

学生4：方程（2）中，a=4，b=1，c=1.

教师：很好！这些方程都有解吗？

一些学生开始动笔求解.

教师：如果不解这三个方程，你能判断它们解的情况吗？

学生（齐）：能！

教师：根据什么来判断呢？

学生5：根的判别式Δ=b2-4ac.

（教师板书：Δ=b2-4ac）

教师：好的！接下来，请自己先判断一下，然后将结果在小组中交流一下.

学生活动：自主判断方程根的情况，并将判断的结果在小组中交流.

5分钟后，教师组织学生开展交流.

学生5：方程（1）有两个不相等的实数根.

教师：你是怎么判断的？

学生6：利用根的判别式，Δ=（-3）2-4×2×0=9＞0，所以这个方程有两个不相等的实数根.

教师：据此，我们可以归纳：当b2-4ac＞0时，方程ax2+ bx+c=0（a≠0）有两个不相等的实数根.（教师板书）

学生7：在方程（2）中，Δ=（-2）2-4×3×1=0，所以方程（2）应该有两个相等的实数根.

（教师板书：当b2-4ac=0时，方程ax2+bx+c=0（a≠0）有两个相等的实数根）

学生8：在方程（3）中，Δ=12-4×1×1=-3＜0，所以方程（3）没有实数根.

（教师板书：当b2-4ac＜0时，方程ax2+bx+c=0（a≠0）没有实数根）

在经历了近10分钟的探索与交流后，“根的判别式”的应用要点被教师板书在黑板上.接下来，教学进入典型例题讲评环节.

2.片断简析

按照知识梳理的顺序，这则片断可以分为两个阶段：第一阶段，归纳给出的三个方程的共同特征，梳理出一元二次方程的一般形式，并剖析每个方程中对应字母a、b、c的取值；第二阶段，学生应用根的判别式判断方程根的情况，教师引导学生归纳出判别式的三个应用要点，并进行板书.整个教学过程，花了近10分钟的时间，在中考一轮复习中，花这么长时间做“这么一点事”，实在有点不值.首先，一元二次方程的一般形式应该在前面课时中已经进行了复习，在这里再拿出来强调，完全没有必要；其次，三个一元二次方程的二次项系数、一次项系数和常数项几乎一眼就能看穿，让学生结合一般形式进行分析实属多余之举，吃力不讨好；再者，这里给出的三个方程，并不是都需要用到根的判别式来判定根的情况的，比如方程（1），目测可得解为x=0，x=，拿这样的方程来讨论根的情况，要么是低估了学生的能力，要么是低估了根的判别式的价值；最后，基础扫描环节，应该侧重于知识的应用，而非知识点的归纳，我们应在教学中让学生说说怎么用这个知识的，上面的教学片段中，教师则侧重于从题目归纳出知识点，有点本末倒置的味道，何况，学生对根的判别式有着较为深刻的认知，几乎每位学生都能准确地说出根的判别式的应用点.因此，不管是从教学时间的损耗上，还是从教学成效上看，教师的板书价值都不大.投影的快速展示，可能比教师的“一笔一画”要来得有效.

二、优化设计及意图

（一）优化设计

1.例题设计

例1下列一元二次方程中有两个不相等的实数根的方程是（）.

A.2x2-x+1=0B.x2+2x-19=0

C.4x2-4x+1=0D.x2+x+1=0

例2关于x的方程kx2-4x-=0有实数根，则k的取值范围是__________.

例3若关于x的方程x2-2x+kb+1=0有两个不相等的实数根，则一次函数y=kx+b的大致图像可能是图1中的（）.

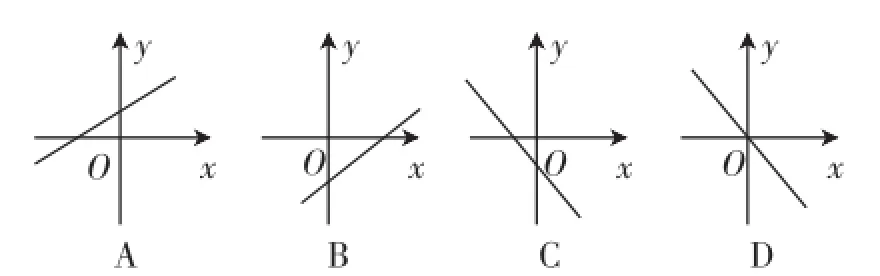
图1

2.教学过程设计

学生自主解答，然后在学习小组中交流解题的结果、所用到的知识和解题的注意点.接下来，教师组织学生进行全班交流，结合具体的题目剖析一元二次方程根的判别式的应用价值.对于例2和例3这些具有一定的综合性的问题，我们将会做具体详细的解题思路的分析，明确一元二次方程根的判别式在什么时间上、以什么方式进入到解题过程中，以及在解题过程中发挥怎样的作用，从而使学生将这一知识与其他数学知识“捆绑”在一起，不再孤立看待.

（二）设计意图

中考前的复习，时间紧，任务重.我们的教学，绝不能停留在“过去的知识简单重复讲”的境地，必须要对课堂教学的内容进行整合，要重点关注数学基础知识在应用上的创新.在例题的选择与设计上，要将单一知识置于整个数学知识系统去观察分析它的价值，从学生分析问题和解决问题的能力上优化提升的角度，去选择和设计具有一定综合性的数学问题作为例题.上面的三道例题，都具有一定的综合性，例1是一元二次方程根的判别式自身的综合，这里出现的四个方程囊括了这一知识的三个常见应用点；例2是一元二次方程根的判别式与一元一次方程的解的综合，解题必须用到分类讨论思想，这让例题的难度得到了一定的提升；例3是一元二次方程根的判别式和一次函数图像的综合，通过判别式的应用可以得出k、b的符号，进而对各个图像进行判断，数与形的结合让例题教学不再是在单一的知识上行进.

接下来说说教学过程的设计，学生先进行自主解答，这是他们头脑内进行的“自觉的革命”，没有任何“外力”的干扰，知识的提取与应用都成为学生自己的事情，这是完全符合中考要求的，也是我们日常教学必须坚持的.至于后续的交流，无论是小组内的，还是全班的，都只是让学生知晓自己思考的结果对与错，以及思维过程的成与败，教师的适度引导和学生间的互助，将会有力地推动学生的思维能力和解题能力不断提升.

三、几点思考

1.“碎片化”复习打断了学生思维的连续性

无论是获取新知，还是解答例题，教师都应给予学生独立思维的时间和空间.数学问题的解决，有时需要合作，但在当下这种教学与考试体制下，更多的还是需要学生的独立思考.走进考场，谁都不可以替代孩子们去思考，去解题.所以，数学课，尤其是中考前的复习课，应将更多的时间留给学生去回忆、去思考、去解题、去整理、去完善.我们绝不能，也不应该将学生的思维活动进行碎片化处理，通过有一搭无一搭的对话来替代学生思考，以教师引领、优生帮忙、软件演示的方式替代每一名学生思考，这不仅是复习课不能出现，恐怕新授课也不能出现.上面的教学片断中，教师的用心是良苦的，他自始至终牢牢掌控着学生思维的进程，没有容许学生出现一点出格的思维或想法，甚至连“（1）2x2-3x＝0”这样一个完全可以直接解就能发现解的情形的方程，也要引导学生从根的判别式角度给出解题过程.为了将课时复习主线凸显出来，这位教师是动了心思的，然而，这样的教学对学生的成长是不利的，尤其不利于学生思维的可持续发展.在问题解决过程中，学生的思维是延续的，而教师采用的这种分段式教学，让学生分段感知一元二次方程的这些基础知识，从一般形式，到各项系数，再到判别式，最后到应用，每一次成果的展示都切断了学生的思维，让学生停下来，享受着教师总结出的丰硕成果.听课过程中，就一个感觉，学生学得累，教师教得更累，这样的片断式教学，还是整合一下，批量教学呈现的效果可能会更好！

2.“新授式”板书延缓了数学知识的网络化

板书是课堂教学的重要组成部分，不同的课型教学的重心不同，板书也应有着较大的差异.新授课应侧重于课时核心知识的展示，板书的最大作用是将抽象归纳出结论，力求共享；复习课应重在多种数学知识的关联，要关注知识“单体”的板书，更要关注知识“单体”之间的联系，以便形成网络化知识体系.显而易见，新授课的板书应该有新授课的特点，复习课板书也就应该有复习课的特点.我们绝不可以用新授课的板书来代替复习课的板书.在我们的复习课上，要力图通过箭头、连线、框格等将知识“单体”链接起来，形成彼此关联的、有效的知识网络.在上面的教学片断中，教师过于重视知识“单体”的呈现，先后将一元二次方程根的判别式的三个应用点完整地书写在黑板上，占了半面黑板，给其他的与本课有关联的知识留下了极小的版面.在教师接下来的教学中，笔者发现他并没有形成知识网络的意识，一节课结束，黑板上除了学生板书的过程，就留下了开头板书的几个知识点.很显然，教师所用的就是新授式板书，他仍然是将知识“单体”作为教学的重点在加以回顾，对该知识与其他知识间的关联视而不见，这将大大延缓数学知识的“网络化”进程.而笔者所进行的优化，则将很多与本节课有关联的知识推上了教学的“前台”，在例1到例3的解答与交流中，我们不仅要板书一元二次方程的根的判别式，还要将其他与此有关联的知识一并板书.当教学进入小结提升环节时，原本孤立的知识通过带箭头和不带箭头两种线串在一起，知识“单体”被紧密链接在一起，至此，一幅能够引发学生产生定向联想的知识结构图已经成形.

3.“综合性”设例凸显了数学知识的整体性

不管是新授课，还是复习课，数学知识都是教学的主要内容.而对数学知识的教学，我们应该把每一个知识都置于整体知识的体系中，要努力“引导学生感受数学的整体性”.就以本文所说的复习课为例，单一的知识我们在新授学习中已经获得了，而且绝大多数同学掌握得比较好，此时，我们就没有必要再在每个个体上花太多时间和精力，要从整体的角度选择一些融合了多种数学知识的问题作为教学的例题，并以例题的解答和交流来引导学生完成数学知识的梳理，让那些原本隐藏着的知识“衔接点”暴露出来，真真正正地成为学生分析问题和解决问题的重要“抓手”.当然，这需要教师充分理解即将复习的内容，知晓这一内容与其他知识之间有着怎样的联系，至少这些联系之间的“亲疏远近”，最终筛选出联系最紧密的、在中考中出现次数多的、能够在课堂上让学生顺利产生关联的知识，这就是接下来选题的方向.茫茫题海，有了方向，我们就可以做出相应的选择，有原题可以选择原题.如果没有适合的原题，我们就改编，从加强知识的纵横联系的角度，将所选择的知识点巧妙地融合到设计的例题中，以求实现“解一题，会一类，通一片”的复习目标.这就是笔者选择例1至例3作为教学例题的原因所在，为了规避“简单化”复习带来的“知识牢牢记住，能力一带而过”的现象，我们不仅重视例题设计的综合性，还重视教学过程的综合性，我们将学生独立思考、小组合作交流、教师引领展示都融合到例题教学过程之中，使例题教学成为一个多人参与、多元互动的立体化教学体系，学生收获知识是我们的期待，但我们更期待通过复习能全面提升学生分析问题和解决问题的能力，只有这个目标实现了，我们的复习才是真正有效的.H