严格直觉模糊熵

范晓诗，雷英杰，李成海，郭新鹏（空军工程大学防空反导学院，陕西　西安710051）

严格直觉模糊熵

范晓诗，雷英杰，李成海，郭新鹏
（空军工程大学防空反导学院，陕西西安710051）

通过对现有直觉模糊熵构造方法的分析，针对隶属度和非隶属度函数相等但直觉指数不同导致熵值无法区分的局限性，借鉴经典数学中严格大于和严格小于的概念，提出了严格直觉模糊熵（strict intuitionistic fuzzy entropy，SIFE）的概念并给出公理化定义。在该定义基础上给出一个SIFE构造方法，然后抽象为一般表达式，使得SIFE的特性在决策排序问题中更加适用。通过算例分析，表明该方法的正确性，与其他直觉模糊熵构造方法比较，说明该方法可以克服存在的局限性。

直觉模糊集；直觉指数；严格直觉模糊熵；决策

网址：www.sys-ele.com

0 引 言

自1986年文献［1］扩展了Zadeh的模糊集理论，提出直觉模糊集以来，该理论得到了不断完善与丰富。直觉模糊集理论中直觉指数（犹豫度）πA（x）的提出描述了事物中立的特征，其相关研究深入到模式识别［2］，决策判断［3-5］，图像［6-7］，医学［7-8］等领域。熵是信息论中刻画信息量不确定性的经典指标，许多学者自然而然将两者进行了有益的结合，文献［9］最早引入直觉模糊熵的公理化定义，随后文献［10］根据该定义给出了一种直觉模糊熵的计算式。一些学者相继在此基础上做了深入研究，其中文献［11-12］根据直觉模糊熵的定义，提出了区间值直觉模糊熵构造方法，将直觉模糊熵推广到区间值直觉模糊范畴，扩展了其应用范围，随后文献［13］根据直觉模糊集距离提出了一种新的区间值直觉模糊熵。文献［14］提出的vague熵构造方法，本质上也是一种直觉模糊熵的等价形式，文献［15］在分析了直觉模糊熵公理化定义后，针对支持与反对证据相等的情况下，原有定义不合理的问题，修改了第一条约束条件，使其更加合理可信。文献［16-17］根据三角函数的特性，充分考虑隶属度、非隶属度和犹豫度的影响，提出基于三角函数的直觉模糊熵构造方法。文献［18］利用直觉模糊熵分析直觉模糊集的不确定性，并提出一种集合分离定理。

直觉模糊决策是直觉模糊理论应用的一大热点，近些年一些文献尝试利用直觉模糊熵或区间直觉模糊熵进行排序或决策［19 21］，通过深入的分析，发现直觉模糊熵公理化定义对于处理形如A=＜a，a＞，a∈［0，0.5］的直觉模糊数排序和决策问题，存在先天不足。一般来讲，多属性条件下的决策方法应当可以处理单属性条件下的决策需求，这里考虑一个极端的例子，当决策属性退化为单一条件时，对于形如x1=＜0.3，0.3＞，x2=＜0.5，0.5＞这样的直觉模糊数进行决策，利用现有直觉模糊熵的构造方法均无法判断。这是因为直觉模糊熵公理化定义中将隶属度与非隶属度相等时的熵值规定为E（A）=1，因而本文认为这样的直觉模糊熵定义不够全面，某些情况下没有严格体现直觉模糊熵的差别，固称这样的直觉模糊熵是非严格的，类似经典数学中“≥”或者“≤”关系，导致结果无法直接运用于排序或决策，所以原有理论存在一定的局限性。文献［20-21］中利用不同的熵值赋权方法处理，其本质是将其他数据的直觉模糊熵值通过一定的计算，赋于无法处理的数据上，从而回避了这些数据对决策结果的影响。因此，本文考虑完善直觉模糊熵公理化定义，使其能够区分更多情况下的直觉模糊熵，即本文所提出的严格概念，将直觉模糊熵推广到更普遍的适用范围，使得直觉模糊数排序和决策方法更加完整和统一。

1 严格直觉模糊熵定义及构造方法

Atanassov［1］给出直觉模糊集的定义如下。

定义1 设X是一个给的论域，那么直觉模糊集合A=｛＜x，μA（x），γA（x）＞|x∈X｝为直觉模糊集，记作IFS（X）。其中μA（x）：X→［0，1］和γA（x）：X→［0，1］分别为A的隶属度和非隶属度函数，且满足对于A上所有x∈X，都有0≤μA（x）+γA（x）≤1，由μA（x）和γA（x）组成的有序区间对＜μA（x），γA（x）＞称为直觉模糊数。

对于X中的每个直觉模糊子集，定义πA（x）=1-μA（x）-γA（x）为A中x的直觉指数或犹豫度。直觉模糊集A的补集定义为

目前公认的直觉模糊熵公理化定义满足如下定义［3］。

定义2 一个映射E：IF S（X）→［0，1］称为直觉模糊熵，如果E满足以下条件：

条件1 E（A）=0当且仅当A是经典集合；

条件2 E（A）=1当且仅当xi∈X，满足μA（xi）= γA（xi）；

条件3 E（A）=E（AC）；

条件4 E（A）≤E（B）对于xi∈X，μA（xi）≤μB（xi）且γA（xi）≥γB（xi），当μB（xi）≤γB（xi）；μA（xi）≥μB（xi）且γA（xi）≤γB（xi），当μB（xi）≥γB（xi）。

如前文所述，目前文献中提到的直觉模糊熵均是基于该定义构造给出，具有一定局限性，而本文从更普遍的角度出发，借鉴经典数学中强调大于“＞”和小于“＜”时，加入严格大于和严格小于的描述，考虑区分隶属度与非隶属相等条件下的直觉模糊熵，提出一种严格直觉模糊熵（strict intuitionistic fuzzy entropy，SIFE）Es的概念，并给出如下定义。

定义3 一个映射Es：IF S（X）→［0，1］称为严格直觉模糊熵，如果Es满足以下条件：

条件1 Es（A）=0当且仅当A=＜1，0＞或A=＜0，1＞；

条件2 Es（a，b）＜Es（a，a）≤1，其中a∈［0，0.5］，b∈［0，1］，a≠b，当且仅当μA（xi）=γA（xi）=0.5时，E（A）=1；

条件3 Es（A）=Es（AC）；

条件4 Es（A）≤Es（B）对于xi∈X，μA（xi）≤μB（xi）且γA（xi）≥γB（xi），当μB（xi）≤γB（xi）；μA（xi）≥μB（xi）且γA（xi）≤γB（xi），当μB（xi）≥γB（xi）。

严格直觉模糊定义中，条件2的意义在于区分形如A=＜a，a＞的直觉模糊熵值，但限定当μA（xi）=γA（xi）时熵值均大于其他μA（xi）≠γA（xi）的情形，这与实际逻辑相符，并且Es（μA（xi）=γA（xi））是关于xi的单调增函数，当μA（xi）=γA（xi）=0.5时Es（A）取最大值1，从而满足直觉模糊数排序及决策判断的需求。例如在该定义的严格直觉模糊熵中，存在直觉模糊数＜0.4，0.4＞，＜0.4，0.5＞和＜0.5，0.5＞，根据定义，新构造直觉模糊熵计算结果应满足E（0.4，0.5）＜E（0.4，0.4）＜E（0.5，0.5）=1。

根据定义3下面给出一个严格直觉模糊熵式。

定理1 给定一个论域U=｛x1，x2，…，xn｝，令A=则A的严格直觉模糊熵为

这里定义σ∈［0，0.5］用来调节E（a，a）的取值范围，使得Es（μA（xi）=γA（xi））∈［1-σ，1］。因为通常认为“相对模糊”和“相对精确”的熵值分界点为0.5，从而保证E（μA（xi）=γA（xi））具有较高的熵值。一般要求σ取值偏向定义域区间的左侧。特别，当σ=0时，该式退化为满足定义2的直觉模糊熵式，从而使该式更具有普遍意义。

下面给出定理1满足定义3（σ≠0）约束条件的证明。

证明 条件1，首先证明充分性，若Es（A）=0时，因为δ（xi）＞σδ（xi）＞σδ（xi）（1-2 min（μ（xi），γ（xi）），可得δ（xi）=0，即|μ（xi）-γ（xi）|=1，也就是μ（xi）=1，γ（xi）= 0或μ（xi）=0，γ（xi）=1；再证明必要性，若μ（xi）=1，γ（xi）=0或μ（xi）=0，γ（xi）=1时，显然有Es（A）=0。

条件2，因为0≤1-|μ（xi）-γ（xi）|＜1，当a＜b时，Es（a，a）=1-σ（1-2a）＞δa，b-σ（1-2a），δa，b-σ（1-2a）＞δa，b-σδa，b（1-2 min（a，b）=Es（a，b），条件成立；

当a＞b时，要证明Es（a，a）=Es（a，b），只需证明1-σ（1-2a）＞δa，b（1-σ（1-2b）），由于δa，b是关于b的单调增函数，只需证明b→a时，即1-σ（1-2a）＞1-σ（1-2b）成立，即1-2a＜1-2b，显然成立；

另外，当Es（A）=1μ（xi）=γ（xi）且1-2 min（μ（xi），γ（xi））=0μ（xi）=γ（xi）=0.5，所以条件2成立。

条件3，显然成立。

条件4，对于xi∈X，当μA（xi）≤μB（xi）且γA（xi）≥γB（xi），即min（μA（xi），γA（xi））≤min（μB（xi），γB（xi）），δ（xA）≤δ（xB），那么

（1-2 min（μA（xi），γA（xi））≥（1-2 min（μB（xi），γB（xi）），即

σ（1-2 min（μA（xi），γA（xi））≥σ（1-2 min（μB（xi），γB（xi）），那么

1-σ（1-2min（μA（xi），γA（xi））≤1-σ（1-2min（μB（xi），γB（xi）），即δA（xi）（1-σ（1-2min（μA（xi），γA（xi）））≤δB（xi）（1-σ（1-2 min（μB（xi），γB（xi））），从而得到Es（A）≤Es（B）。同理，当μB（xi）≥γB（xi）时该条件也成立。证毕

例：A1=＜0.3，0.6＞，A2=＜0.4，0.4＞，A3=＜0.7， 0.1＞，取4位有效数字，根据式（1）得+0.980 0+0.230 0）=0.575 6。

2 严格直觉模糊熵一般式

根据本文给出的定理（1）可以直观的看出，为了达到区分形如A=＜a，a＞的直觉模糊熵值，所构造的式包括两部分，第一部分是基本直觉模糊熵函数，可借鉴现有构造方法，第二部分通过σ修正E（A）熵值，使其映射在一定范围内，这样严格直觉模糊熵构造方法可用抽象为如下：

式中，f（xi）是普通直觉模糊熵函数，根据这样的构造原理，这里我们可以不加证明的给出几个其他构造方法，如更一般的严格直觉模糊熵函数，记作：

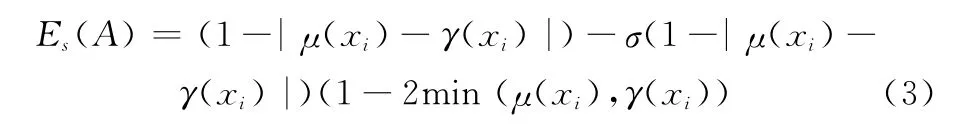
根据文献［15］可以构造严格直觉模糊熵：

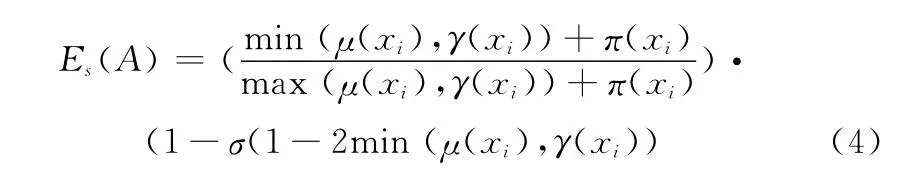
根据文献［17］可以构造一个基于三角函数的严格直觉模糊熵如：

这里取σ=0.1，可以得到式（1）的函数图像如图1所示，式（3）～式（5）的函数图像分别如图2～图4所示。通过图像可以看出，式（3）函数呈线性，式（1）和式（4）较为平滑，而式（5）熵值收敛速度较快。这些直觉模糊熵的构造方法分布大体相同，同时均能满足本文给出的定义3，可以适用于不同条件下的需求。

图1 式（1）示意图

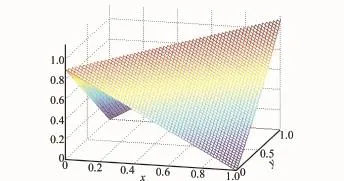
图2 式（3）示意图

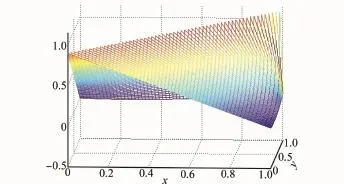
图3 式（4）示意图

图4 式（5）示意图

3 算例分析

通过分析可以发现，现有文献提供的算例中数据类型不够全面，如文献［19］中算例出现两次＜0.5，0.5＞的直觉模糊数，却没有其他隶属度与非隶属度相同但直觉指数不同情况，而文献［17］中不包括隶属度或非隶属为0的情况，这样不利于检验直觉模糊熵的边界值，所以本文认为算例中应该包括更全面的数据类型。

首先，假设要对一个多属性直觉模糊集方案X进行识别决策，认为平均直觉模糊熵值最小的方案识别度最高，即最优。这里共有3种决策方案，每种决策方案各有4个属性值，如表1所示。表中数据包括隶属度与非隶属度相同但直觉指数不同情况，也包括非隶属度为0、直觉指数为0等情况。特别地，如＜0.3，0.3＞表示隶属度和非隶属度相等，但支持和反对方面均得不到充分的证据，这符合客观实际中存在的某种现象。

表1 决策方案直觉模糊数

利用本文提出的严格直觉模糊熵构造方法进行计算，得到各属性熵值如表2所示。

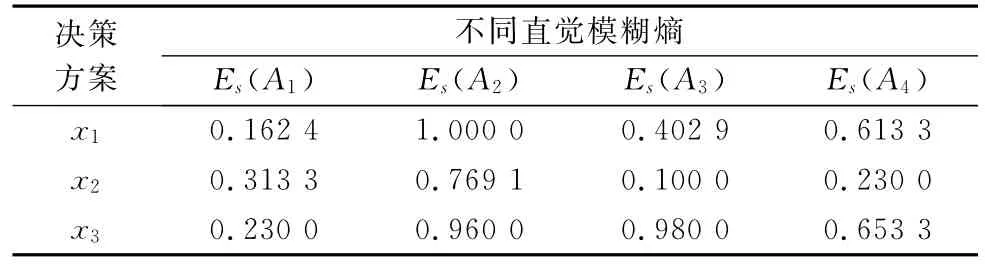
表2 严格直觉模糊熵计算结果

对所求结果取平均值得到Es（x1）=0.544 6，Es（x2）= 0.353 1，Es（x3）=0.705 8，最终得出方案x2优于方案x1优于方案x3的决策结果。

为了反映不同直觉模糊熵值计算方法存在的局限性，接着分别利用文献［14-15］和文献［17］中提出的直觉模糊熵计算方法对表1中的直觉模糊数进行处理，其中Es为本文方法计算的熵值，最后得到对比结果如表3所示。

表3 与其他直觉模糊熵比较

从表3的结果可以看出，利用本文计算的严格直觉模糊熵方法与其他文献的方法比较，均能得到相同的排序结果，从而证明了该方法的正确性。

最后，当本算例中属性退化为仅有A2时，分别计算直觉模糊熵值如表4所示。

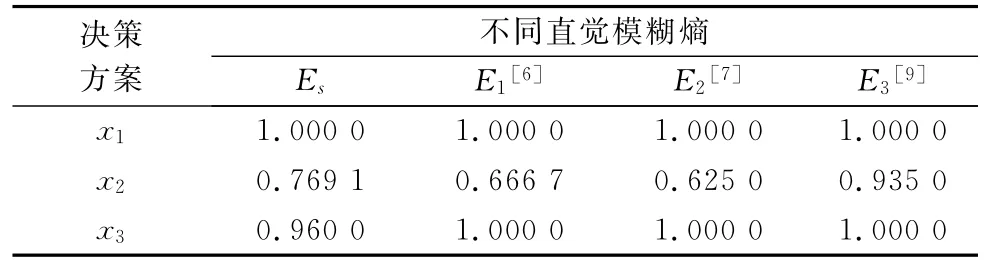
表4 退化后直觉模糊熵决策比较

通过表4可以看出，文献［14-15］和文献［17］中的方法只能得到E（x2）＞E（x1）=E（x3）的结论，不能进行严格排序，说明在某些情况下，原有直觉模糊熵的计算方法具有一定的局限性，而相关文献中无论是利用专家系统或多属性权重计算，都回避了不能比较的数据。而本文提出的严格直觉模糊熵对直觉模糊数进行了熵值严格处理，即使在仅有单一属性的条件下依旧可以得到正确的决策结果，说明严格直觉模糊熵本质上具有决策判断的特征，使得直觉模糊熵理论具有更广泛的应用能力。

4 结 论

本文通过分析现有直觉模糊熵构造方法，发现在对隶属度和非隶属度相等但直觉指数不同的直觉模糊数进行排序和决策判断中存在不足，提出严格直觉模糊熵的概念，完善了直觉模糊熵公理化定义，并给出一个基于新定义下的严格直觉模糊熵构造方法并抽象为更一般的表达式。通过算例分析并和其他直觉模糊熵构造方法进行对比，证明该方法的正确性和合理性，同时克服了原有理论的局限，将其推广到更一般的情况。类似地，区间值直觉模糊熵也可参照该方法进行定义、构造和应用。

［1］Atanassov K.Intutionistic fuzzy sets［J］.Fuzzy Sets and Systems，1986，20（1）：87-96.

［2］Mao J J，Yao D B，Wang C C.A novel cross-entropy and entropymeasures of IFSs and their applications［J］.Knowledge-Based Systems，2013，48（8）：37-45.

［3］Qin J D，Liu X W.Study on intervalintuitionisticfuzzy multi-attribute group decision making method based on choquet integral［J］. Procedia Computer Science，2013，17（5）：465-472.

［4］K haleie S，Fasanghari M.A n intuitionistic fuzzy group decision making method using entropy and association coefficient［J］. Soft Com puting，2012，16（7）：1197-1211.

［5］K ucukvar M，G u m us S，Egilmez G，et al.Ranking the sustainability performance of pavements：an intuitionistic fuzzy decision making method［J］.Automation in Construction，2014，40（15）：33-43.

［6］Pedro M P，Pedro C，H u m berto B，et al.Image seg mentation using atanassov’s intuitionistic fuzzy sets［J］.E xpert Systems with A pplications，2013，4（1）：15-26.

［7］Chaira T.A rank ordered filter for medicalimage edge enhancement and detection using intuitionistic fuzzy set［J］.A pplied Soft Com puting Journal，2012，12（4）：1259-1266.

［8］Jaganathan P，K uppucham y R.A threshold fuzzy entropy based feature selection for medical database classification［J］.Com puters in Biology and M edicine，2013，43（12）：2222-2229.

［9］Burillo P，Bustince H.Entropy on intuitionistic fuzzy sets and interval-valued fuzzy sets［J］.Fuzzy Sets and Systems，1996，78（3）：305-316.

［10］Szmidt E，Kacprzyk J.Entropy for intuitionistic fuzz sets［J］. Fuzzy Sets and Systems，2001，118（3）：467-477.

［11］Zeng WY，Li HX.Relationship between similarity measure and entropy of interval-valued fuzzy sets［J］.Fuzzy Sets and System，2006，157（11）：1477-1484.

［12］Zhang H Y.Zhang W X，Mei C L.Entropy ofinterval-valued fuzzy sets based on distance and its relationship with simi larity measure［J］. Knowledge-Based Systems，2009，22（6）：449-454.

［13］Farhadinia B.A theoretical develop ment on the entropy of interval-valued fuzzy sets based on the intuitionistic distance and its relationship with similarity measure［J］.K nowledge-BasedSystems，2013，39（2）：79-84.

［14］Zhang Q S，Jiang S Y.A note on information entropy measures for vague sets and its application［J］.Inform ation Sciences，2008，178（21）：4184-4191.

［15］W ang Y，Lei Y J.A technique for construction intuitionistic fuzzy entropy［J］.Control and Decision，2007，12（12）：1390-1394.（王毅，雷英杰.一种直觉模糊熵的构造方法［J］.控制与决策，2007，12（12）：1390-1394.）

［16］Ye J.T wo effective measures ofintuitionistic fuzzy entropy［J］. Com puting，2010，87（1/2）：55-56.

［17］W ei C P，Gao Z H，Guo T T.An intuitionisticfuzzy entropy measure based on trigonometricfunction［J］Controland Decision，2012，27（4）：571-574.（魏翠萍，高志海，郭婷婷.一个基于三角函数的直觉模糊熵式［J］.控制与决策，2012，27（4）：571-574.）

［18］Pal N R，Bustince H，Pagola M，et al.Uncertainties with atanassov’s intuitionistic fuzzy sets：fuzziness and lack of knowledge［J］.Information Sciences，2013，228（10）：61-74.

［19］Wang J Q，Wang P.Intuitionistic linguistic fuzzy multi-criteria decision-making method based on intuitionisticfuzzy entropy［J］.Controland Decision，2012，27（11）：1694-1698.（王坚强，王佩.基于直觉模糊熵的直觉语言多准则决策方法［J］.控制与决策，2012，27（11）：1694-1698.）

［20］Zhang Y J，M a P J，Su X H.Multi-attribute decision making with uncertain attribute weightinformation in the framework of interval-valued intuitionistic fuzzy set［J］.Acta Automatica Sinica，2012，38（2）：220-228.（张英俊，马培军，苏小红.属性权重不确定条件下的区间直觉模糊多属性决策［J］.自动化学报，2012，38（2）：220-228.）

［21］Chen X H，Dai Z J，Liu X.Approach to interval-valued intuitionistic fuzzy decision making based on entropy and correlation coefficient［J］.Systems Engineering and Electronic，2013，35（4）：791-795.（陈晓红，戴子敬，刘翔.基于熵和关联系数的区间直觉模糊决策方法［J］.系统工程与电子技术，2013，35（4）：791 -795.）

Strict intuitionistic fuzzy entropy

F A N Xiao-shi，L EI Ying-jie，LI Cheng-hai，G U O Xin-peng
（Air and Missile Defense College，Air Force Engineering University，Xi’an 710051，China）

Methods of intuitionistic fuzzy entropy are analyzed.Considering the classical mathematic concepts of strict greater-than and strictless-than，a concept strictintuitionistic fuzzy entropy（SIF E）and an axiomatic definition are proposed by solving defect that entropy of the degree of membership function equals the degree of none-mem bership function but different intuitionistic indexes cannot be distinguished.A technique for constructing the SIF E based on this definition is proposed and an expression is abstracted.The SIF E is m ore adaptive in decision and sorting.The validity is certified by the example and the limitis overco med by co m paring to other methods.

intuitionistic fuzzy set；intuitionistic index；strict intuitionistic fuzzy entropy（SIF E）；decision

T P 391

A

10.3969/j.issn.1001-506 X.2016.03.20

1001-506 X（2016）03-0602-05

2015-01-07；

2015-09-10；网络优先出版日期：2015-09-28。

网络优先出版地址：http：//w w w.cnki.net/kcms/detail/11.2422.T N.20150928.1036.012.html

国家自然科学基金（61272011）；陕西省自然科学青年基金（2013JQ8031）资助课题

范晓诗（1988-），男，博士研究生，主要研究方向为网络信息安全。

E-mail：fan_xs@126.com

雷英杰（1956-），男，教授，博士，主要研究方向为网络信息安全、智能信息处理。

E-mail：leiyj ie@163.com

李成海（1966-），男，教授，硕士，主要研究方向为网络信息安全、智能信息处理。

E-mail：lichengh@126.com

郭新鹏（1985-），男，讲师，硕士，主要研究方向为智能信息处理。

E-mail：305221885@qq.com