弹道导弹中段诱饵微动特性研究

王伟林，陈 磊，雷勇军（国防科学技术大学航天科学与工程学院，湖南　长沙410073）

弹道导弹中段诱饵微动特性研究

王伟林，陈 磊，雷勇军
（国防科学技术大学航天科学与工程学院，湖南长沙410073）

微动辨识是弹道导弹中段目标识别领域的研究热点，目标的微动特性与其结构、质量分布、初始状态和受力状态密切相关，将根据给定诱饵的重量、几何特性、释放初始状态等，建立诱饵进动、自旋、章动等微运动模型，对微动模型进行深入研究和理论推导，分析得到释放后诱饵的姿态角变化特性、自旋周期、章动角、章动角速率和欧拉角等微运动特征。仿真结果表明文中建立的微动模型，可以有效的对弹道导弹中段诱饵的微动特性进行分析，对比与弹头微运动特征的差异，可以有效的为弹道中段目标识别提供依据。

微动；弹道导弹中段；目标识别；模型；诱饵；弹头

网址：www.sys-ele.com

0 引 言

弹道导弹的突防技术是指弹道导弹为无损伤地通过反导防御系统拦截区，在助推段、中段、末段所采取的对付敌方反导防御系统一切探测拦截手段的技术，是衡量弹道导弹武器系统战术技术性能和武器研制水平的重要标志。包括诱饵技术、弹头隐身、有源干扰技术、弹头机动技术、多弹头技术等。突防方经常一起使用多种突防措施以达到良好的突防效果［1-2］。

在弹道导弹飞行中段，大气极为稀薄，可以认为导弹是在真空中飞行，此段弹道的射程和飞行时间占全弹道的80%～90%以上，因此容易遭到自动寻的导弹的跟踪拦截。在中段防御上，美国导弹防御局采用国家导弹防御计划中已验证的技术，进行了多次地基防御拦截试验和海基防御拦截试验。通过大量的飞行试验搜集各类弹头和诱饵的运动特性，根据导弹飞行过程中呈现的预期特征，建立了匹配识别的特征模板库，并在拦截试验中对不同目标的运动特性的识别能力进行验证［3］。

可见导弹目标的特性研究对目标识别起到至关重要作用。而目前对诱饵等目标特性的分析主要集中在对轨道特性的分析，缺少对微动特性的分析。微动特性是指诱饵除质心平动以外的运动，如自旋、进动、章动等。中段飞行过程中，弹头和诱饵的轨道特征差异不大，微动特性有较大区别，通过微多普勒效应分析，可以识别出弹头和诱饵［4］。

近年来，微动得到了广泛的关注，微动辨识成为弹道目标识别领域的研究热点［5-8］，如文献［9］研究了不同形式雷达信号对微动导弹目标的特征提取技术，文献［10］分析了雷达观测下的目标摆动模型，文献［11-12］分析了锥形目标的微动模型及其微多普勒，但都是基于文献［13-14］提出的锥形目标的自旋模型和锥旋模型，文献［15-17］也对微动模型开展了部分研究和微多普勒仿真验证。上述研究都没有对微动模型进行深入研究和理论推导，目标的微动特性与其结构、质量分布、初始状态和受力状态密切相关，鉴于中段突防诱饵释放于大气层外，本文将参照航天器姿态运动理论［18］，根据给定诱饵的重量、几何特性、释放初始状态等，建立诱饵进动、自旋、章动的微运动模型，分析释放后诱饵的姿态角变化特性、自旋周期、章动角等微运动特征，并分析与弹头微运动特征的差异，从而为弹道中段目标识别提供依据。

1 微动动力学模型

不受外力矩情况下，体坐标系内建立的绕质心转动方程为

式中，ω为诱饵瞬时转动角速度矢量；角动量矢量H=Iω；I为诱饵相对于质心的惯量张量矩阵

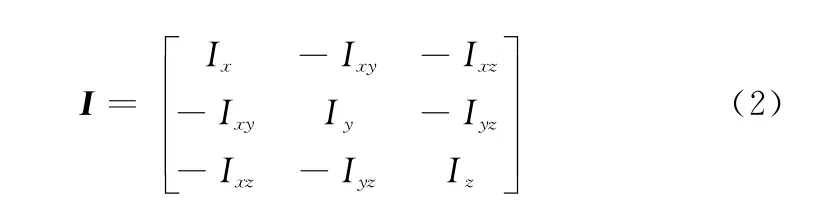
式中，将Ixx，Iyy，Izz简化为Ix，Iy，Iz表示。如果三体轴均为惯量主轴，则其姿态动力学方程可简化为

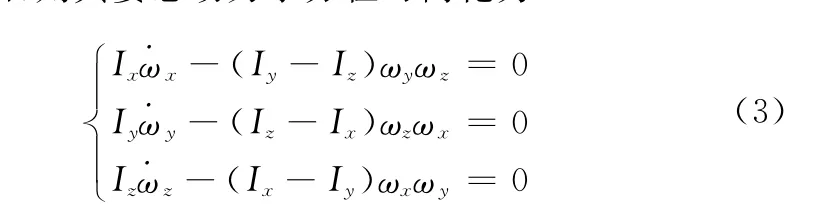
2 微动特性分析

设体坐标系的三轴为刚体对质心的惯量主轴，Ix，Iy和Iz为相应的主惯量，惯量积等于零。假定仿形轻诱饵对自旋轴oxB是轴对称的［19］，绕通过质心的横轴的横向惯量都相等，Iy=Iz。

由式（3）第一个方程得出ωx等于常值，所以诱饵的自旋运动是独立的，与横向运动没有耦合作用。令Iz=Iy= It，ωx=ωs，Ωn=（Ix/It-1）ωs，动力学方程简化为

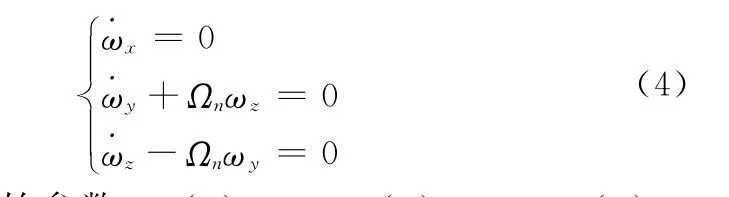
设置积分初始参数：ωx（0）=ωs，ωy（0）=ωy0，ωz（0）= ωz0，则式（4）解为

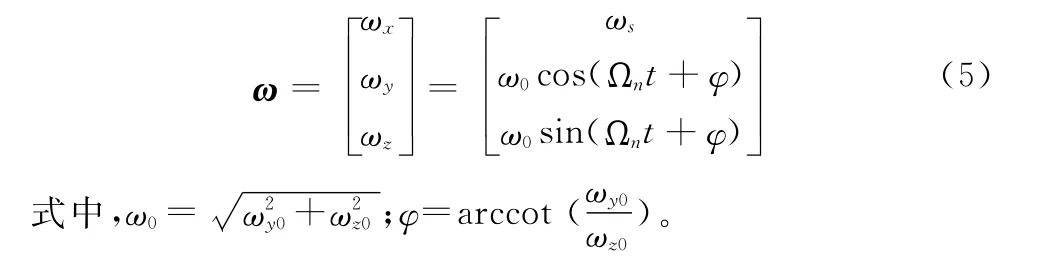
在本体坐标系中，角速率分量ωy，ωz周期性的变化，周期为2π/Ωn，自旋转速始终为常数ωs。ωy，ωz的合成角速率矢量ωt，称为横向角速率矢量，幅值为横向角速率矢量ωt绕oxB轴旋转，转速为Ωn，因此诱饵的瞬时转速ω绕自旋轴作圆锥运动，图1给出了诱饵自旋瞬时转速分解的示意图。

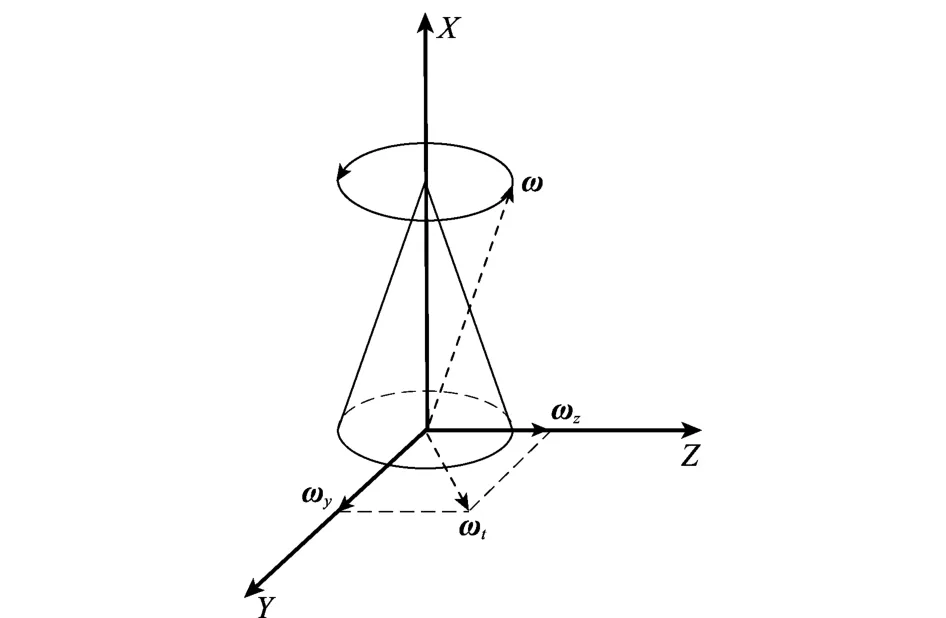
图1 诱饵自旋特性示意图

在本文中假定锥形诱饵高1.5 m，半径0.5 m，质量为M= 1 kg。转动惯量Ix=0.075，Iy=Iz=0.122。Iy=Iz＞Ix，因此Ωn＜0，转速ω做圆周运动的方向和自旋转速ωx反向。

为进一步说明诱饵自旋轴的运动规律，定义空间中固定的角动量矢量为

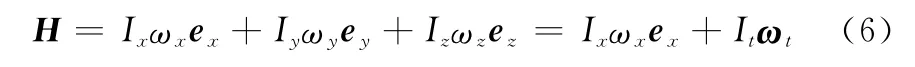
角动量矢量H由横向、轴向两部分组成，因为这两部分旋转着的矢量的合成矢量H在空间中定向，因此由于横向角速率ωt绕自旋轴旋转，导致自旋轴也作圆锥运动。因此合并式（5）和式（6），可以将瞬时转速矢量ω投影为

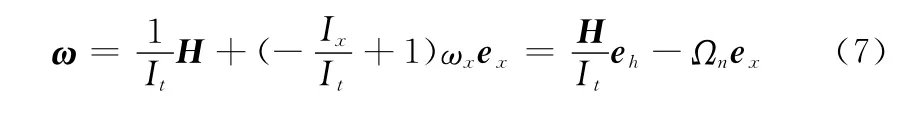
式中，eh为沿角动量方向的单位矢量。

ω矢量将同时做两种圆锥运动：一种是绕诱饵主惯量轴x的圆锥运动（本体锥），转速为Ωn，称为本体章动速率；另一种是绕角动量H做的圆锥运动（进动，空间锥），旋转速度是Ω=H/It，称为空间章动速率。诱饵的姿态运动是诱饵绕自旋轴旋转，同时本体锥在空间锥滚动。由式（7）知ω、H、x这3矢量共面，自旋轴也绕角动量H做圆锥运动，速率为Ω，x轴与H的夹角θ称为章动角。如果章动角随时间不变化，则诱饵的运动是进动。如果章动角随时间波动，则诱饵的运动称为章动，即章动是在进动的基础上再加上章动角的波动［20］。

章动角的计算公式为

式（8）说明轴对称自旋诱饵的章动角是常值，所以如果诱饵具有轴对称性，章动等同于进动。角动量由轴向角动量Ixωx和横向角动量Itωt，他们之比等于章动角的正切，

上文给出了诱饵在体坐标系下的微动特性分析，下面研究诱饵在发射惯性系下的绕质心运动方程。首先，给出发射惯性系与诱饵本体坐标系（弹体坐标系）的欧拉角关系图，如图2所示。

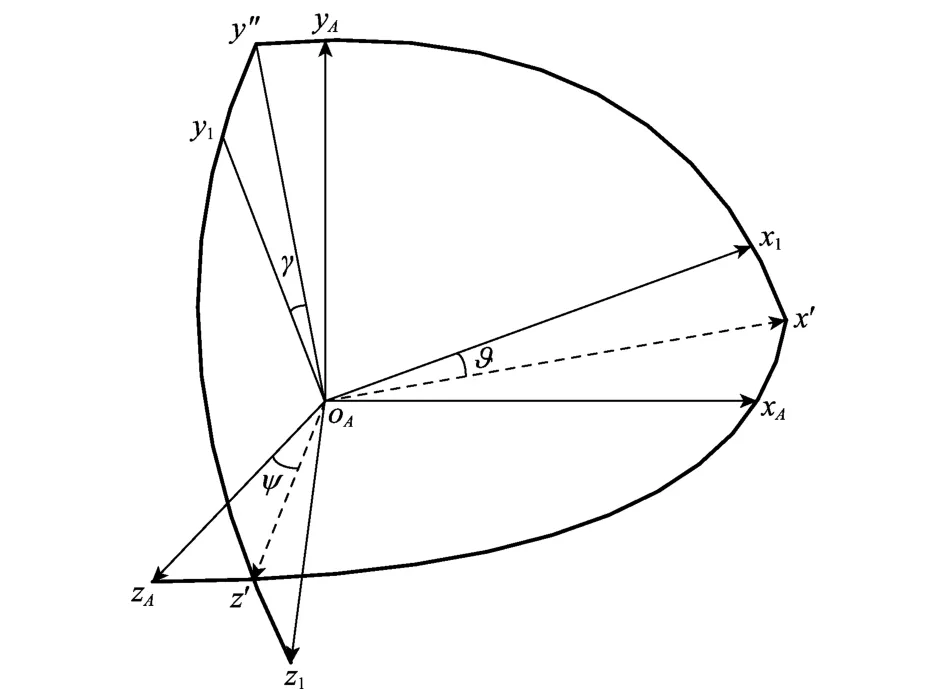
图2 发射惯性系与弹体坐标系的转换

依据图2给出发射惯性系A与弹体坐标系B之间的转换。弹体按先偏航、再俯仰、后滚动的“yzx”旋转顺序，从发射惯性系旋转至弹体坐标系，偏航角为、俯仰角为、滚动角为γ。BA表示由A系到B系的转移矩阵，AB表示由B系到A系的转换矩阵，则有［21］

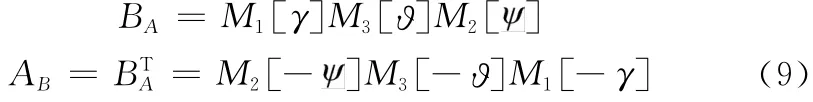
以k0，k1，k2表示yA，z′，x1方向的单位矢量，体坐标系是由发惯系作3次转动形成，转动角速度为，，γ，根据角速度的矢量合成法则，刚体在惯性系的角速度为

以体坐标系中矢量表示的角速度：

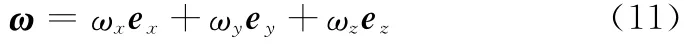
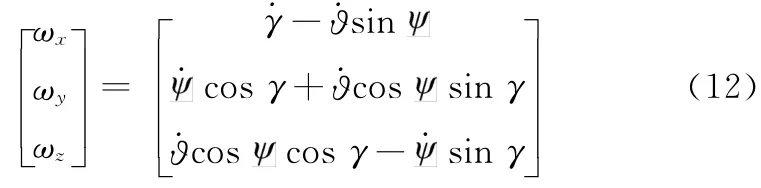
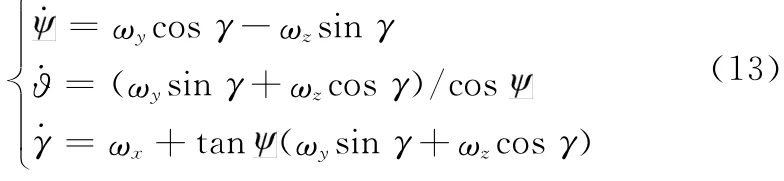
结合第2节中求得的式（4）：

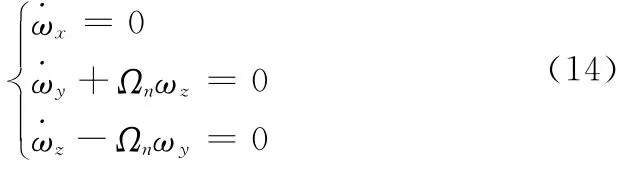
联立求解上述微分方程，可以得到诱饵在发射惯性系中俯仰角、偏航角、滚动角的值。

3 仿真算例

3.1 诱饵微动特性求解

本节给定初始值，求解对应的微动参数。仿真初始参数设置如下：则求得其转动惯量：

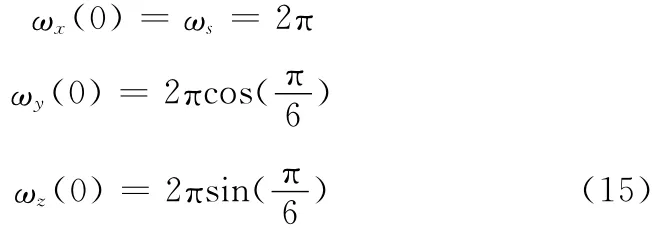
式中，Iz=Iy＞Ix。

从而求得其章动角速率：

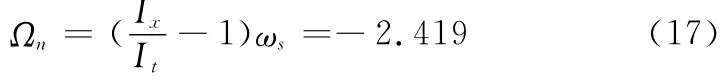
由式（5）得到在本体坐标系中角速率的分量：

从而求得角速率大小为：|ω|=8.89 rad/s。

由式（8）知，轴对称自旋诱饵的章动角是常值：

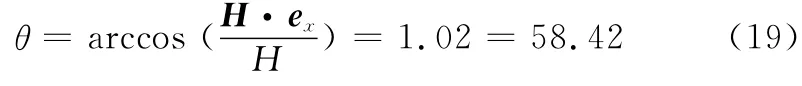
空间章动速率：

3.2 诱饵微动特性影响因素

为分析诱饵释放时的初始角速率对诱饵的微动运动的影响，本节将改变初始参数，并分析其影响。

（1）首先对沿y，z轴方向的初始释放角速率的影响进行分析。因为

假定诱饵绕各轴的转动惯量以及ωs，φ等参数不变，令ω0取值从0逐步增加到5π，看对应的章动角、本体章动角速率、空间章动角速率的变化情况。

由图3～图5的变化曲线可以看出，随着初始角速率ω0的增加，章动角θ变大，本体章动角速率对应Ωn保持不变，空间章动角速率Ω逐渐变大，验证了式（20），当θ∈［0 π/2］时，θ和Ω有相同变化趋势。

图3 章动角变化规律曲线图

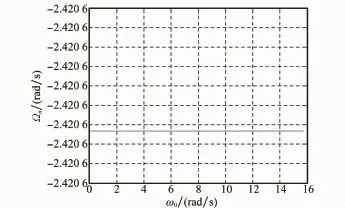
图4 本体章动角速率变化规律曲线图

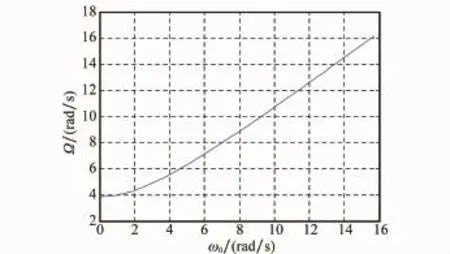
图5 空间章动角速率变化规律曲线图

（2）下面研究当诱饵绕各轴的转动惯量以及ω0，φ参数不变，自旋转速ωs取值从0～5πrad/s时，对应的章动角θ、本体章动角速率Ωn、空间章动角速率Ω的变化情况。

图6～图8分别给出了章动角、本体章动角速率、空间章动角速率的变化曲线。随着自旋转速ωs的增加，章动角逐渐变小，本体章动角速率逆向增大，空间章动角速率逐渐增加。

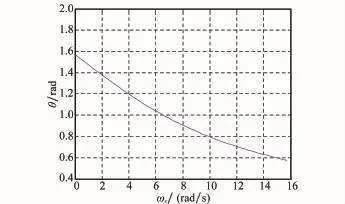
图6 章动角变化规律曲线图

由图3和图6对比可知，转速ωs和ω0增大，对章动角的影响是相反的，侧面反映诱饵飞行稳定性的变化。

3.3 弹头微动特性求解

自旋稳定的弹头，由于弹箭分离以及诱饵释放时的横向干扰，弹头在中段飞行中将发生进动。

弹头的初始角速度要低于诱饵的角速度，锥形弹头高1.5 m，半径0.5 m，参照图1，质量为M=100 kg，转动惯

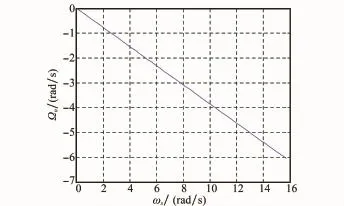
图7 本体章动角速率变化规律曲线图

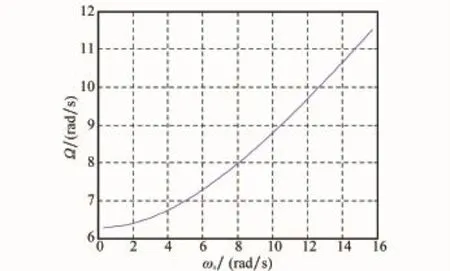
图8 空间章动角速率变化规律曲线图

因此弹头的横向转动惯量和纵向转动惯量均很大，在受到横向干扰时，弹头比诱饵更容易保持稳定，其进动角通常较小。同时因为Iz=Iy＞Ix，因此Ωn＜0，转速ω做圆周运动的方向和自旋转速ωx反向，对旋转对称目标而言，自旋运动不会产生微多普勒效应。

仿真初始参数：

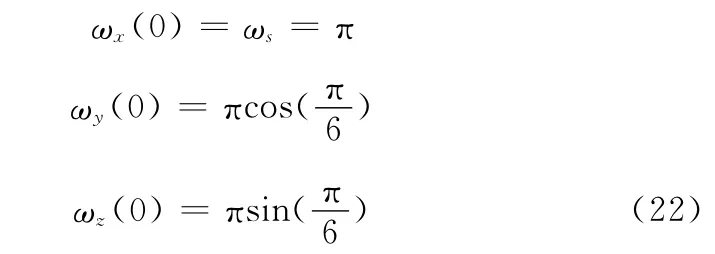
因为转动惯量Iz=Iy＞Ix，从而求得其章动角速率：

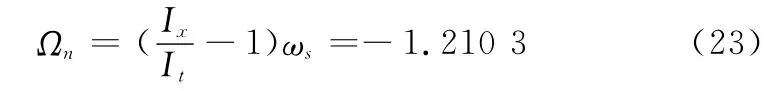
得到在本体坐标系中角速率的分量：

由式（24），求得本体坐标系中角速率大小为

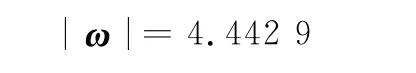
轴对称自旋诱饵的章动角是常值：

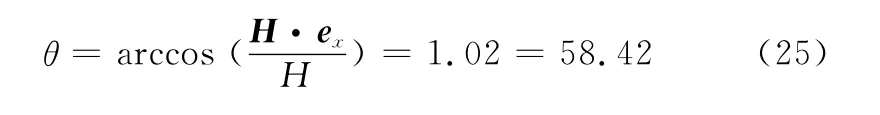
空间章动速率：

因为设计的仿形轻诱饵与弹头外形相同，虽然两者转动惯量差别较大，但因为3个方向转动惯量的比值相同，其章动角的大小是相同的。但考虑到其给定的初始角速率不等，由式（23）知，其章动角速率并不相同，可以作为弹头和诱饵识别的依据。

如果诱饵不是仿形诱饵，其转动惯量不是对应成比例，则其章动角、章动角速率等参数也存在差别，因此会更易于雷达识别。

3.4 发射惯性系下欧拉角的求解

下面求解发惯系下的欧拉角，设置仿真初始参数如下：

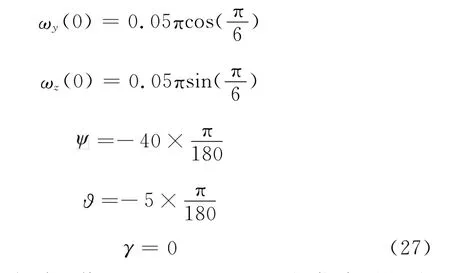
令ωx（0）分别取值0.1π，0.5π，2π，选择仿真时间为50 s。

下面给出不同初始条件下的仿真结果，并进行对比分析。

图9～图11给出了诱饵在发射惯性系中俯仰角、偏航角、滚动角随时间的变化曲线。图12～图14给出了诱饵在弹体系中转动速率随时间变化曲线。由以上各图可以发现，初始时刻绕诱饵主轴的自旋转速影响诱饵的俯仰角和偏航角变化周期和最大幅值，初始转速越大，其周期越短，幅度变化越小，而滚动角的累加效果越明显。

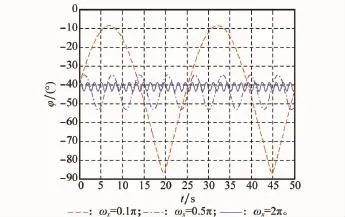
图9 诱饵俯仰角的变化曲线

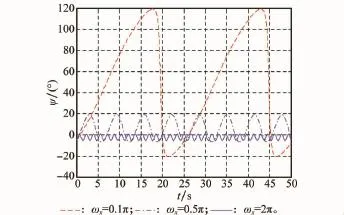
图10 诱饵偏航角的变化曲线

图11 诱饵滚动角的变化曲线图

图12 诱饵沿X轴转动速率

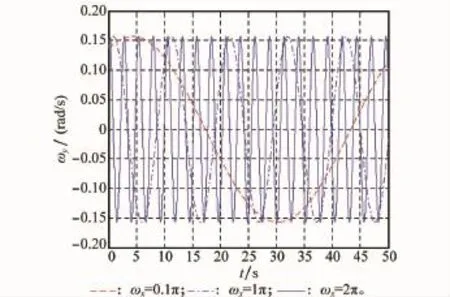
图13 诱饵沿Y轴转动速率图

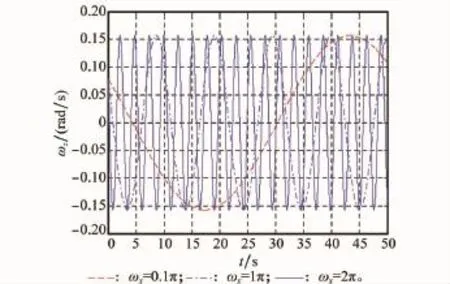
图14 诱饵沿Z轴转动速率

4 结 论

本文基于航天器姿态动力学与控制理论，建立了轴对称仿形轻诱饵的一般性微运动模型，根据给定诱饵的重量、几何特征和释放的初始状态等，解析推导得到释放后诱饵的姿态角、自旋周期、章动角、章动角速率以及发惯系下欧拉角等微动参数。通过仿真，研究了初始参数改变后，诱饵微动特性的变化，验证了公式的正确性；并对比了同形状弹头的微动特性，两者微动特征存在的差异可以为弹道中段目标识别提供依据。

［1］H u B，Li Z.Key penetration technologies and develop ment of abroad ballistic missile［J］.Tactical Missile Technology，2010，26（2）：124-128.（胡波，李壮.国外弹道导弹突防的关键技术与发展［J］.战术导弹技术，2010，26（2）：124-128.）

［2］Fetter S，Sessler AM，Cornwal l J M，et al.Countermeasures：a technical evaluation of the operational effectiveness of the planned US national missile defense system［M］.M A：U nion of Concerned Scientists MIT Security Studies Program，2000.

［3］United States Department of Defense.Ballistic missile defense review report［R］.Washington，2010.

［4］Camp WW，Mayhan J T，O’Donnell R M.Wideband radarfor ballistic missile defense and range Dopplerimaging of satellites［J］.Lincoln Laboratory Journal，2000，12（2）：267-280.

［5］Chen V C.Advances in applications of radar micro-Doppler signatures［C］∥Proc.of the IE E E Conference on Antenna M easurements&A pplications，2014：1-4.

［6］Clemente C，Balleri A，W oodbridge K，et al.Develop ments in target micro-Doppler signatures analysis：radar imaging，ultrasound and through-the-wall radar［J］.E U R A SIP Journal on A dvances in Signal Processing，2013，2013（1）：1-18.

［7］Stankovic L，Thayaparan T，Dakovic M，et al.Micro-Doppler rem ovalin the radarimaging analysis［J］.IE E E Trans.on Aerospace and Electronic Systems，2013，49（2）：1234-1250.

［8］Jung J H，Kim K T，Kim S H，et al.Micro-Doppler extraction and analysis of the ballistic missile using R D A based on the real flight scenario［J］.Progress in Electromagnetics Research M，2014，37：83-93.

［9］Liu LH，Des M，M ounir G，et al.Ballistic missile detection via micro-Doppler frequency estimation fro mradar return［J］. Elsevier Digital Signal Processing，2012，22（1）：87-95.

［10］Lei P，Liu YX，Li K L.Micro-motion identification and maximum swing angle estimation of cone-shaped wobbling targets［J］.Systems Engineering and Electronics，2013，35（8）：2258-2262.（雷鹏，刘永祥，李康乐，等.摆动锥体运动辨识及最大摆动角估计［J］.系统工程与电子技术，2013，35（8）：2258-2262.）

［11］Zhang J K，Dai D H，Xing S Q，et al.Analysis ofin SA R 3D imaging characteristics of target with rotational micro-motion［J］. Journal of Astronautics，2014，35（3）：345-355.（张静克，代大海，刑世其，等.旋转微动目标InSA R三维成像特性分析［J］.宇航学报，2014，35（3）：345-355.）

［12］Gao H W，Xie L G，W en S L，et al.A nalysis and extraction of micro Doppler induced by cone shaped target’s wobbling［J］. Chinese Journal of Electronics，2008，36（12）：2497-2502.（高红卫，谢良贵，文树梁，等.摆动锥体目标微多普勒分析和提取［J］.电子学报，2008，36（12）：2497-2502.）

［13］Chen V C，Li F Y，H o S S，et al.Micro-Doppler effectin radar phenomenon，model and simulation study［J］.IE E E Trans.on Aerospace and Electronic Systems，2006，42（1）：2-21.

［14］Chen V C.T he micro-Doppler effect in radar［M］.M A：Artech House，2011.

［15］Sun Y J，Fu Y，Cheng Z，et al.Q uaternion based micro-Doppler simulation of ballistic targets［C］∥Proc.of the IE T International Radar Conference，2013：80-85.

［16］Wang T，Wang X，Chang Y，et al.Estimation of precession parameters and generation of ISAR images of ballistic missile targets［J］.IE E E Trans.on Aerospace and Electronic Systems，2010，46（4）：1983-1995.

［17］Lei P，Wang J，Sun J.Analysis of radar micro-Doppler signatures from rigid targets in space based on inertial parameters［J］.IE T Radar，Sonar&Navigation，2011，5（2）：93-102.

［18］Markley F L，Crassidis J L.Fundamentals of spacecraft attitude determination and control［M］.New York：Springer，2014.

［19］Chen F Y，Zhao L，Zhang Q G，et al.Profile m odeling light decoy spatial attitude control design［J］.Modern Defense Technology，2010，38（4）：83-87.（陈方予，赵蕾，张其刚，等.仿形轻诱饵空间定姿初探［J］.现代防御技术，2010，38（4）：83-87.）

［20］Zhang R W.Spacecraftattitude of dynamics and control［M］. Beijing：Press of Beihang University，1998.（章仁为.卫星轨道姿态动力学与控制［M］.北京：北京航空航天大学出版社，1998.）

［21］Siouris GM.Missile guidance and control systems［M］.New York：Springer Science&Business Media，2004.

Micro-motion analysis of decoy in midcourse of ballistic missile

WANG Wei-lin，C H E N Lei，LEI Yong-jun
（College of Aerospace Science and Engineering，National University of Defense Technology，Changsha 410073，China）

Micro-motion identification of the decoy in midcourse of ballistic missile has aroused general interest in current society，and decoy’s structure，quality distribution，initial state and externalforce are essential to the micro-motion property of the decoy.The micro-motion model of the decoy，including the self-spin，procession and nutation，is established based on the quality，geometrical character and initially released state.With a deep research into the micro-motion model and theoretical derivation，the change rate of the attitude angle，self-spin period，nutation angle and nutation angle rate are achieved.Numerical simulations demonstrate the effectiveness of the proposed approach，which can act as a basis for the targetidentification in comparison with the micro-motion property of warhead.

micro-motion；midcourse of ballistic missile；target identification；model；decoy；warhead

TN95

A

10.3969/j.issn.1001-506 X.2016.03.02

1001-506 X（2016）03-0487-06

2014-11-21；

2015-05-07；网络优先出版日期：2015-09-29。

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20150929.1111.002.html

国家自然科学基金（11372345）资助课题

王伟林（1988-），男，博士研究生，主要研究方向为飞行器动力学与制导控制。

E-mail：wangweilin@nudt.edu.cn

陈 磊（1974-），男，教授，博士，主要研究方向为拦截动力学与制导控制、空间目标碰撞预警。

E-mail：clwhl@263.net

雷勇军（1968-），男，教授，博士，主要研究方向为计算固体力学理论与应用。

E-mail：leiyj108@nudt.edu.cn