基于Radon-MDCFT的空间高速机动目标检测与参数估计方法

吴仁彪，马 頔，李 海（中国民航大学天津市智能信号与图像处理重点实验室，天津300300）

基于Radon-MDCFT的空间高速机动目标检测与参数估计方法

吴仁彪，马 頔，李 海
（中国民航大学天津市智能信号与图像处理重点实验室，天津300300）

提出一种基于Radon-修正离散线性调频傅里叶变换（Radon-modified discrete chirp Fourier transform，RMDCFT）的空间高速机动目标检测与参数估计的方法。该方法在目标运动参数范围内进行搜索，将目标数据从距离单元-慢时间域中取出并进行相应匹配变换处理，在补偿回波数据相位并进行相参积累以用于目标检测的基础上同时得到目标速度和加速度的估计结果。该方法能同时对距离徙动和多普勒走动进行校正，并可在脉冲数有限和低信噪比下有效地检测到空间高速机动目标并获得较好的参数估计结果。仿真结果和对所提方法的输出信噪比表达式的数学推导结果证明了所提方法的有效性。

空间目标；距离徙动；多普勒走动；目标检测；参数估计

网址：www.sys-ele.com

0 引 言

空间目标包括空间中的卫星、导弹、空间碎片等，近年来随着空间目标数量急剧增加，其对飞行器的发射、在轨的安全运行和国土防空都造成了较为严重的威胁。所以对空间目标进行探测并获取目标参数信息，从而及早发现来袭的空间目标并为预警提供长的时间就变得尤为重要［1］。天基雷达以卫星作为平台，能够为空间目标探测和深空成像等功能的实现提供可能。它具有监视范围广、实时性强、作战有效性和生存能力高等特点，并且天基雷达能够探测到现有雷达系统无法达到的深广范围，不受地形和国土面积的限制［2］；所以天基雷达将成为未来监视雷达发展的必然趋势。目前只有美国和俄罗斯具有相对完善的空间监视网，随着对空间目标进行探测任务的日益紧迫，建设国家独立的空间监视网将变得愈加重要［2］。

天基雷达探测的空间目标通常具有较高运动速度和加速度，如弹道导弹在主动段火箭巨大的推力作用下速度可以达到7 000 m/s，空间碎片速度则可以达到10 k m/s；短距空空导弹的最大过载超过50 g，中距空空导弹加速度可以达到20 g［3］。由于所探测的空间目标的运动特点，目标的回波信号在雷达相干处理时间内会产生距离徙动和多普勒走动的问题；同时由于所探测的目标距离雷达较远且处于高速运动状态，雷达接收到的目标回波信号较为微弱且对于目标的探测时间相对有限［2］，所以在低信噪比和有限的相干处理时间内，如何有效地实现对存在距离徙动和多普勒走动的目标回波信号进行能量积累成为天基雷达探测空间目标和估计目标参数要解决的关键问题。

谱峰跟踪方法［4］、最小熵法［5］和包络相关对齐方法［6］是3种常用的包络对齐方法；它们对目标回波信号信噪比要求较高，在天基雷达接收到的微弱回波信号情况下难以获得较好的包络对齐效果。而Keystone变换方法［7］在目标存在加速度时，校正距离徙动的效果会受到影响。

文献［8］提出了Radon-傅里叶变换（Radon-Fourier transform，RFT）方法，该方法能够沿着目标在距离单元-慢时间域中的轨迹进行能量积累，但常规的RFT方法只能用于无加速度目标的检测和速度参数估计，其对于机动目标无法获得较好的检测和参数估计效果。

Wigner-Vi l le分布［9］方法能够对多普勒走动进行补偿，但该方法是一个非线性运算，且存在交叉项的干扰。文献［10-11］提出了分数阶傅里叶变换（fractional Fourier transform，FRFT）和Radon-FRFT（RFRFT）方法，在回波信号出现距离徙动和积累脉冲数有限时，回波信号在分数阶域内的能量聚敛性较低，故两个方法不能有效的补偿多普勒走动［12］。

文献［13］提出了离散线性调频傅里叶变换（discrete chirp Fourier transform，DCFT）方法用于补偿信号多普勒走动。该方法要求回波信号的慢时间采样点数为质数且调频参数为整数，实际中难以满足上述条件，其实用性会受到限制。文献［14］提出修正离散线性调频傅里叶变换（modified discrete chirp Fourier transform，MDCFT）方法，虽然它消除了DCFT对信号采样点数和调频参数的限制，实用性得到提高，但是该方法只能对无距离徙动的回波数据进行多普勒走动补偿，当天基雷达接收回波存在距离徙动时，该方法无法获得较好的多普勒走动补偿效果。综上所述，上面讨论的补偿回波信号多普勒走动的方法不能对空间目标获得较好的检测和参数估计效果。

本文提出一种基于Radon-修正离散线性调频傅里叶变换（Radon-modified discrete chirp Fourier transform，RMDCFT）的空间高速机动目标检测与参数估计方法。该方法对机动目标的回波数据进行相参积累，能够在积累脉冲数有限和低信噪比情况下有效地检测出空间高速机动目标，并获得较好的目标参数估计结果。仿真结果证明了所提方法的有效性。另外本文还通过推导所提方法的输出信噪比表达式，说明了所提方法在雷达积累脉冲数较少时能够获得较好的检测性能和准确的目标参数估计结果的原因。

1 回波信号模型

设天基雷达接收的高速机动目标回波信号为

式中，Ar为回波信号幅度；c为电磁波的传播速度；p（·）为回波包络；t′为快时间；tm=m Tr为慢时间；m=0，1，…，M-1；M为相干积累脉冲数；Tr为脉冲重复周期；fc为载波频率为目标与雷达之间的距离；R0为目标的初始距离；v0为目标运动速度；a0为目标加速度。将r（tm）表达式代入式（1）可以得到

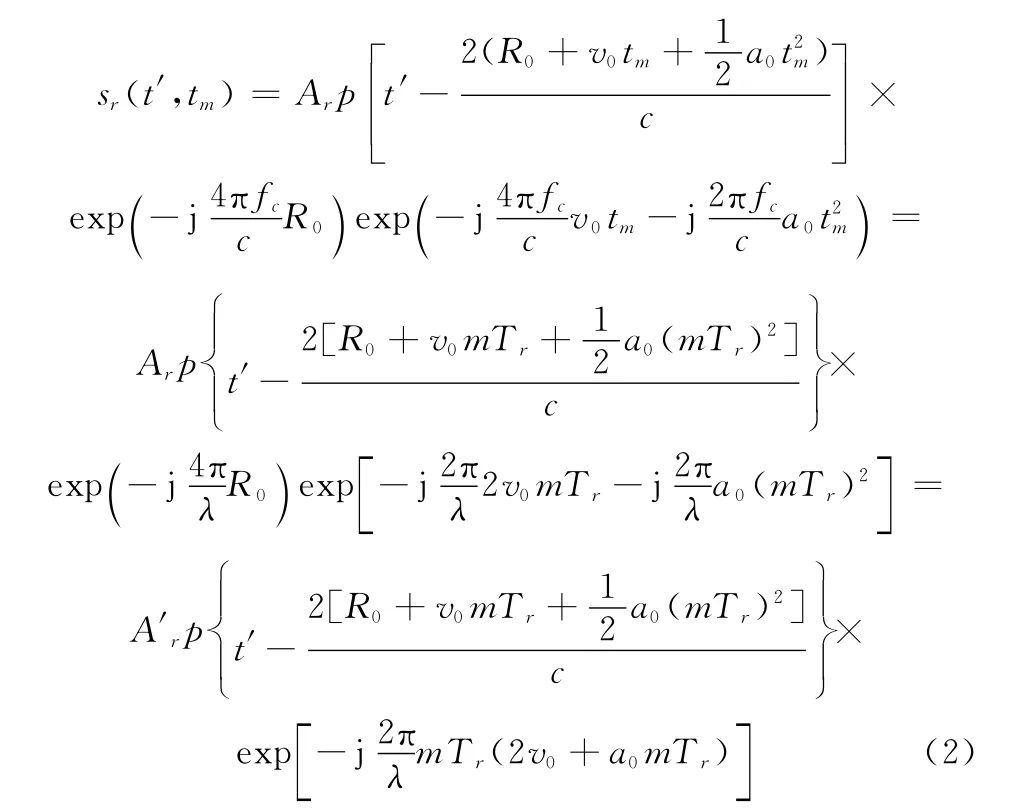
当目标加速度不变时其回波为线性调频信号［11］，从式（2）中可以看出，当目标作匀加速运动时会导致目标回波信号出现距离徙动的现象。

回波信号的多普勒频移为

2 基于R M D CFT的空间高速机动目标检测与参数估计方法

常规R F T算法能沿呈直线型的目标轨迹对相应的回波数据进行相参积累；但当目标存在加速度时回波信号在距离单元-慢时间域中的轨迹是一条二次曲线［9］，此时常规RFT方法失效，无法对目标的回波数据进行相参积累［11］。另外由于加速度的存在导致目标回波信号出现二次相位项，因此需要对其进行补偿，才能有效地积累高速机动目标的回波能量而用于后续的检测和参数估计。

本文提出一种空间高速机动目标检测与参数估计的新方法。该方法在目标的初始距离、速度和加速度搜索区间内对目标参数进行搜索，能沿存在距离徙动的目标轨迹取出数据并进行相应的匹配变换处理，在得到匹配处理输出的峰值基础上实现目标检测，并完成对目标速度和加速度的估计。下面介绍所提算法的原理和实现流程。

2.1 算法原理

为了方便讨论所提算法的原理，先假设目标参数（R0，v0，a0）已知，并针对该参数用RMDCFT算法对回波数据进行处理。

为将目标信号分散在不同距离单元和多普勒单元中的能量进行有效地积累，首先把目标参数（R0，v0，a0）代入到r（tm）中计算出目标轨迹，则此组目标参数（R0，v0，a0）对应的每个脉冲回波信号采样数据所在的距离单元位置可写为［8］

式中，Δr表示雷达距离分辨率；round［·］表示向最近整数进行取整处理［8］。则每个脉冲回波信号的采样数据在距离单元-慢时间域内的位置坐标为［IM（m），m］（m=0，…，M-1）。根据获得的每个脉冲回波信号采样数据在距离单元-慢时间域内的坐标［IM（m），m］（m=0，…，M-1），可将目标回波数据取出以形成一个数据矢量sM，表示为

为了更好地实现目标回波数据的相参积累，需要对式（2）中出现的一次相位和二次相位进行补偿，以实现对回波信号多普勒走动地补偿；相应的补偿函数表示为

对获得的目标回波数据sM用式（6）进行相位补偿后进行相参积累，积累结果［14］可表示为

对式（7）取模可得

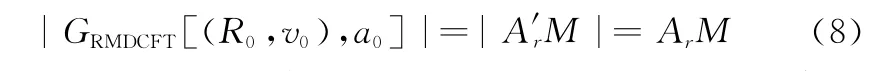
由式（8）可以看出当（R0，v0，a0）为目标所对应的真实参数时，能够对目标回波数据获得最大的积累效果［14］。实际中可利用此特性完成目标检测并对未知的目标参数进行估计。

由于实际中目标参数未知，因此需要对目标的初始距离、速度和加速度参数进行搜索；构造代价函数

式中，Ri，vq，aj分别代表在目标初始距离、速度和加速度3个参数范围内相应的搜索值。则使代价函数式（9）取得最大值时所对应的，即为目标速度和加速度的估计结果［15］。

2.2 算法实现流程

图1为本文所提方法的实现流程图，具体步骤可描述如下。

步骤1 利用参数组合（Ri，vq，aj），根据式（5）所示的方法在距离单元-慢时间域内确定一条轨迹，并将该轨迹所对应的回波数据取出。

步骤2 将取出的回波数据按式（7）所示的方法进行相参积累，对相参积累结果取模。

步骤3 利用式（9）得到目标速度和加速度的估计结果。为了降低运算量，采用变步长搜索［15］的方式进行处理。

图1 本文方法实现流程图

3 仿真结果与分析

通过计算机仿真验证本文所提方法的有效性。仿真参数设置如下：信噪比为-10 dB，脉冲重复频率为1 500 Hz，积累脉冲数为64，信号带宽为30 M Hz，载频为1 G Hz，目标初始位于第400个距离单元中，初始速度v0=3 000 m/s，加速度a0=180 m/s2。

图2所示为回波信号经过脉冲压缩处理后的结果。从图2中可以看到目标回波信号出现距离徙动现象。图3为分别利用MTD、RFT、FRFT和RFRFT方法对回波数据进行处理后的结果。从图3（a）和图3（b）中可以看出MTD、RFT方法都无法对存在距离徙动和多普勒走动的回波数据进行相参积累，经处理后目标信号仍然淹没在噪声中，因此两种方法无法有效地进行目标检测与参数估计。从图3（c）和图3（d）中可知，F R F T方法不能对存在距离徙动的回波数据进行相参积累；而RFRFT虽然能够对高速机动目标的回波数据进行相参积累，但是在脉冲数较少时，回波数据在分数阶域内的聚敛性较低［12］，故两种方法也很难获得较好的目标检测和参数估计性能。图4为应用本文提出的RMDCFT变换方法对回波数据进行处理后的结果。

图2 脉冲压缩处理后的结果图

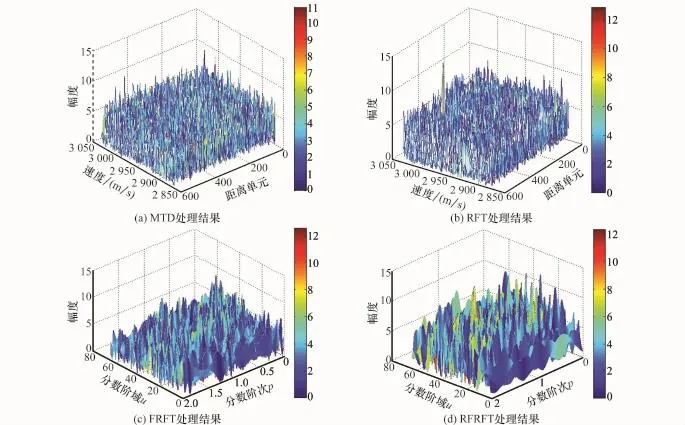
图3 不同方法对回波数据处理的结果

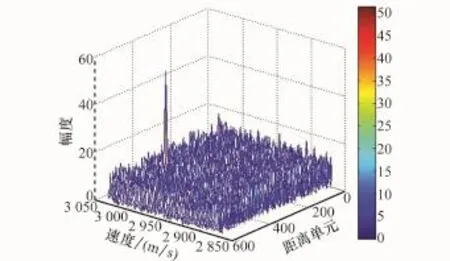
图4 本文方法对回波数据的处理结果

由图4可以看出，回波数据经过本文所提方法处理后，回波能量得到了有效积累，在距离单元-速度域内能够形成明显的积累峰值；结合仿真结果和本文所提算法的输出信噪比表达式（推导证明过程见本文的第4节）可知本文方法能够在积累脉冲数有限和低信噪比下有效的检测到目标并获得较好的参数估计结果［13，16］。

图5是分别在虚警概率为Pfa=10-4和Pfa=10-6时，做2 000次蒙特卡罗实验后得到的各个方法的检测性能曲线。

从图5（a）中可以看出，在输入信噪比分别在8 dB和2 dB左右时，M T D方法和R F T方法的检测概率Pd=0.9；在输入信噪比分别为-1 dB和-5 dB时，FRFT方法和RFRFT方法的检测概率Pd=0.9，而本文提出的RMDCFT方法能有效地将目标信号进行相参积累，在低信噪比、积累脉冲数有限的情况下能有效地检测到目标，在输入信噪比约为-13 dB时，本文方法的检测概率Pd=0.9。从图5（b）中也能看出本文方法能够在较低的信噪比下获得较高的检测概率，检测性能优于其他方法。

图5 不同方法的检测性能比较结果

图6（a）是不同方法估计得到的目标速度均方根误差随输入信噪比变化的曲线图，图6（b）是RMDCFT、RFRFT和FRFT方法估计得到的目标加速度均方根误差随信噪比变化的曲线图。本文方法对于速度和加速度估计的均方根误差和其他方法相比能更接近CRB；其估计性能优于其他方法，从而进一步验证了本文所提方法的有效性。

图6 目标参数估计的均方根误差随信噪比变化图

为了分析采用取整运算进行距离徙动校正对算法处理结果的影响，下面将分别采用插值方法和取整方法实现距离徙动校正后的目标检测和参数估计性能进行对比。

插值方法和取整方法的目标检测和参数估计性能对比结果分别如图7和图8所示。

图7 插值方法与取整方法的检测性能比较结果

图8 插值方法与取整方法的参数估计性能比较结果

从图7和图8中可看出，采用取整方法进行距离徙动校正时可获得与插值方法校正距离徙动相当的性能［8，11］；即采用取整运算进行距离徙动校正对算法结果的影响较小［16-17］。

表1给出了插值方法和取整方法进行距离徙动校正后再进行参数估计的运算时间对比结果。计算机配置为处理器：Intel（R）Xeon（R）E5-1650 v3；主频：3.50 G Hz，3.50 G Hz；内存：32.0 GB；仿真软件环境为：M ATL AB R2013a。

表1 算法运算时间比较

由表1可知，在获得和插值方法相当的性能时，取整方法的运算量相对较低。

4 RMDCFT算法的输出信噪比表达式推导

根据文献［11］中关于对算法输出信噪比表达式的定义以及RMDCFT算法的定义式；可定义RMDCFT算法输出信噪比的表达式为

式中

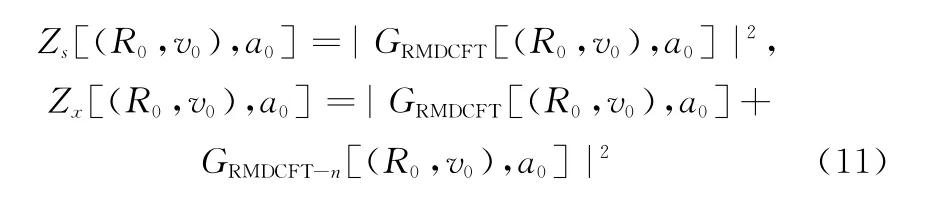
式中，GRMDCFT［（R0，v0），a0］是在目标的初始距离、速度和加速度参数都正确匹配的基础上对目标回波数据进行RMDCFT变换的结果；GR MDCFT-n［（R0，v0），a0］表示目标的初始距离、速度和加速度参数均匹配的基础上对零均值高斯白噪声的采样数据进行RMDCFT变换的结果；var［·］代表求方差；则由RMDCFT变换的定义式有

式中

从瑞丽分布，且|n（m）|2=a2+b2，令

其中有a～N（0，1），b～N（0，1），所以

根据式（19），能得到

故可以进一步得到

从式（23）中可知本文所提方法的输出信噪比高于RFRFT的输出信噪比［11］，从而能够提高检测概率［18］并获得较好的参数估计结果。

5 结 论

本文提出一种基于RMDCFT的空间高速机动目标检测与参数估计方法。该方法通过对目标的距离、速度和加速度的搜索，能够沿着目标在距离单元-慢时间域内的轨迹取出目标回波数据而进行相参积累；接着根据相参积累后的结果完成目标检测和参数估计。结合仿真结果和第4节中的数学证明可知，本文方法在积累脉冲数有限且低信噪比下较常规的MTD方法、RFT方法、FRFT方法和RFRFT方法有更好的检测性能，并也能取得比其他方法更精确的参数估计结果，从而验证了本文所提方法的有效性。

［1］Tirpak J A.T he space based radar plan［J］.Air Force Magazine，2002，85（8）：63-66.

［2］Ma L.Space based radar target detection technology［M］.Bei j ing：Publishing House of Electronics Industry，2013：21-22.（马林.空间目标探测雷达技术［M］.北京：电子工业出版社，2013：21-22.）

［3］Zhao F.Study on detection techniques of tracking and guiding radars in ballistic missile defense［D］.Changsha：National University of Defense Technology，2007.（赵峰.弹道导弹防御跟踪制导雷达探测技术研究［D］.长沙：国防科学技术大学，2007.）

［4］Wang L，Zhu Z D.New range align mentalgorithm for ISAR based on maximum modified kurtosis［J］.Journal of Nanjing University of Aeronautics&Astronautics，2006，38（6）：722-726.（汪玲，朱兆达.一种基于最大修正峰度的ISAR距离对准算法［J］.南京航空航天大学学报，2006，38（6）：722-726.）

［5］Xing M D，Su J H，W ang G Y，et al.New parameter estimation anddetection algorithm for high speed small target［J］.IE E E Trans.on Aerospace and Electronic Systems，2011，47（1）：214-224.

［6］Chen C C，Andress H C.Target motion induced radar imaging［J］. IEEE Trans.on Aerosapce and Electronic Systems，1980，16（1）：2-14.

［7］Sun G C，Xing M D，Xia X G，et al.Robust ground moving-target imaging using deramp-keystone processing［J］.IE E E Trans.on Geoscience and Remote Sensing，2013，51（2）：966-982.

［8］Xu J，Yu J，Peng Y N，et al.Radon-Fourier transform for radar target detection，I：generalized Doppler filter bank［J］.IE E E Trans.on Aerospace and Electronic Systems，2011，47（2）：1186-1202.

［9］Wang Y，Jiang Y C.ISA R imaging of maneuvering target based on the L-class of fourth-order complex-lag PWVD［J］.IE E E Trans.on Geoscience and Remote Sensing，2010，48（3）：1518-1527.

［10］White P R，Locke J.Performance of methods based on thefractional Fourier transform for the detection of linear frequency modulated signals［J］.IE T Signal Processing，2012，6（5）：478-483.

［11］Chen X L，Guan J，Liu N B，et al.Maneuvering target detection via radon-fractional fourier transform-based long-time coherent integration［J］.IE E ETrans.on Signal Processing，2014，62（4）：939-953.

［12］Chen X L，Guan J，H uang Y，et al.Radon-linear canonical am biguity function-based detection and estimation method for marine target with micro motion［J］.IE E E Trans.on Geoscience and Remote Sensing，2015，53（4）：2225-2240.

［13］Xia XG.Discrete chirp-Fourier transform and its application to chirp rate estimation［J］.IE E E Trans.on Signal Processing，2000，48（11）：3122-3133.

［14］Fan P Y，Xia X G.Two modified discrete chirp Fourier transform schemes［J］.Sciencein China Series F，2001，44（5）：329-341.

［15］Zhan L X，Tang Z Y，Zhu Z B.Keystone transform and M D CF T-based detection and parameter estimation for maneuvering weak targets［J］.Acta Aeronautica et Astronautica Sinica，2013，34 （4）：855-863.（战立晓，汤子跃，朱振波.基于Keystone变换和MDCFT的高机动弱目标检测与参数估计［J］.航空学报，2013，34（4）：855-863.）

［16］Xu J，Xia X G，Peng S B，et al.Radar maneuvering target motion estimation based on generalized radon-Fourier transform［J］. IE E E Trans.on Signal Processing，2012，60（12）：6190-6200.

［17］Tian J，Cui W，W u S.A novel method for para meter estimation of space m oving targets［J］.IE E E Geoscience and Remote Sensing Letters，2014，11（2）：389-393.

［18］H e Y，Guan J，Meng X W，et al.Radar target detection and C F A R processing［M］.2nd ed.Beij ing：Tsinghua University Press，2011：12-13.（何友，关键，孟祥伟，等.雷达目标检测与恒虚警处理［M］.2版.北京：清华大学出版社，2011：12-13.）

Space maneuvering target detection and parameter estimation based on Radon-MDCFT

WU Ren-biao，M A Di，LI Hai
（Tianjin Key Lab for Advanced Signal Processing，Civil Aviation University of China，Tianjin 300300，China）

A new method which is know n as Radon-modified discrete chirp Fourier transform（RMDCFT）is proposed to detect the space target and obtain the target’s parameters.The R MDCF Talgorithm can obtain the data of the echo fro m the range unit-slow time do main by searching the target’s motion parameters，then the corresponding transformation processing can be made.After that，the CF A R detection algorithm can be used and the target’s velocity and acceleration can also be obtained.This method can solve the range cell migration and Doppler frequency migration problems，and it is able to obtain the good estimation’s performance.This method is capable of detecting the target under the low S N R background.The performance of the proposed algorithm is verified through the numerical simulations and the mathematical derivation about the RMDCFT’s output signal-to-noise ratio expression which is given.

space target；range cell migration（R C M）；Doppler frequency migration（D F M）；target detection；parameter estimation

TN957.51

A

10.3969/j.issn.1001-506 X.2016.03.03

1001-506 X（2016）03-0493-08

2015-03-18；

2015-06-25；网络优先出版日期：2015-09-25。

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20150925.1647.006.html

国家自然科学基金（61231017，61471365，61571442）；中央高校基本科研业务费项目（3122015B002）；中国民航大学蓝天青年学者培养经费资助课题

吴仁彪（1966-），男，教授，博士，主要研究方向为自适应阵列信号处理、空时自适应处理、探地雷达信号处理。

E-mail：rbwu@cauc.edu.cn

马 頔（1990-），男，硕士研究生，主要研究方向为天基雷达空间微弱目标检测与参数估计技术。

E-mail：Dirac_madi@163.co m

李 海（1976-），男，副教授，博士，主要研究方向为自适应信号处理、动目标检测、干涉合成孔径雷达信号处理。

E-mail：haili@cauc.edu.cn