"考据"精神:数学课堂教学及评价应有的境界---基于两节观摩课的思考

江苏省连云港市教育科学研究所　孙朝仁

"考据"精神:数学课堂教学及评价应有的境界
---基于两节观摩课的思考

"考据"又谓考证,原本是一种治学方法,其本质是不能把想象当作事实,不可把观感当作结论,必须凭证据说话,进行符合逻辑的分析.把它借用到数学教学及评价中则转化为一种追本溯源、正本清源、端本澄源的思维求探过程.这里的"追本溯源"就是关注知识的连续性;"正本清源"就是关注知识的关联性;"端本澄源"就是关注知识的完备性.这些重连续、究关联、求完备的教学与评价行为,正是数学教学不可或缺的"考据"精神,而基于知识获得层面的记得、晓得、明得就是考据过程的价值外显.就这个层面而言,求实、求证、求是的"考据"精神是数学教学理应培植的"推演"意识,能缩短思维过程与结论理解的距离,进而让域内知识通体透明.

本文是笔者观摩"同底数幂的乘法""图形的旋转"两节课后的探微思考与思想凝练,试图在追求完美结论的课堂背景下张扬理性的"考据"精神,让课堂因沉稳而走向精进.

一、考据精神是师生主体评课应有的境界

1.学生评课:考据精神外显的主体

教学评价的话语权一直是教师和科研专家的专利,学生在这一领域是失语的,这就势必造成教学设计与学习主体在一定层面出现"脱节"现象.因为教学面对的对象是活生生的人,人的思维劳动不具有"取现"性,知识掌握的情况在短时效应的视域内是不可考量的.就这个层面而言,教师的教学行为是盲目的.怎样才能实现教学效用的最大化,让教学行为贴着学生的思维地带行走呢?这就要求评课中必须有学生的声音,方能让课堂真正成为学生的学堂,也才能让教学闪耀着难能可贵的考据精神.学生声音的叠加能有效规避教学预设中的"走偏"现象,使得教学走进学生的"最近发展区",而学生的思维声音带有自然性,具有一是一、二是二的"求真"意识,不具有成人世界的面子工程,这就让教学多了一份真实,进而可以提升课堂教学的效度.

笔者在本次课堂观察中反思"本我"视界(学生的思维吞吐量是巨大的,改变了笔者认同"学生资格不够"的观点),认为在课堂教学中适度切入学生评课的视角,可以让教学多一些考据的行为,多一份求甚解的作为.具体操作如下:(1)课堂伊始,让学生提炼本节课待学内容提纲,以此考据学生的求实思维;(2)课堂中段,让学生在思维洗练过程的末端,切入逆向思考的视角(你能写出类同的例子吗?),以此考证学生的求是思维(概念的类化:同底数幂的乘法法则);(3)课堂终端,让学生在整合知识的过程中因呼应和回应而显化评课的隐性视角,以此考究学生的求证思维.这些操作流程的嵌入可能让你的课堂少练了几道题,但提升了思维的透明度,充满了追本溯源的考据精神,课堂效度是毋庸置疑的.为人师者无不体认到,一轮书教下来,什么都会了;上岗前,做题如山,依然有无法克服的思维死角.因此,课堂评价必须介入学生的声音,方能发挥主体的能动作用,让数学课堂因考据而效度满满.

2.教师评课:考据精神显化的核心

评课是教学环节的继续,包括教师自我评课和科研专家的点评.前者是教师对课堂教学的即时反思,具有考据精神,试图在求真的层面上多一份作为;后者是对各级各类公开课、展示课的批注与评注,其间不乏"人情"问题,进而让评课视界出现人为的失真现象,使得课堂因缺乏合理策略的引领而趋于"无进"状态,缺失了课堂潜进的考据精神,使得教师课程执行力的外扩成为一句空话.这样的评课是要被革除的,有害而无益.执教者在"叫好声"一片的场景中,基本上处于"失我"状态,很难用考据的精神去反思教学的种种缺失,专业进步在这里无从谈起,这种异化的评课方式违背了考据的精神,也背离了裴光亚先生在"评课者的情怀"中倡导的实事求是精神.喜欢听赞美之辞是人之常情.但是,不深思成功背面的那些遗憾就会失去潜进的契机和动力.因此,笔者更欣赏评课中的考据精神.基于这样的理念,从理论视角,对本次观摩课提出两点建议,试图能让执教者和在场教师获得一种哲学视角(最容易上的课往往是最难上的,"同底数幂的乘法"归属于容易上的课型),拓宽专业视野,积淀教学的条件性知识(教育教学理论),让教学符合学生的认知规律和现代教学论.同时,让教师有能力接受不同的声音,进而涵养教育者应有的博大胸襟.对"同底数幂的乘法"课堂教学提出:一是概念的同化和顺应必须切入逆向思考的视角,方能让概念属性得以类化(比如:请写出一个能反映同底数幂乘法运算的算式,并求解且标注每一步的运算依据);二是思维过程和结论理解之间是有距离的,必须穿插学生的思路回流和教师的思维外扩,方能让知识敞亮通透(比如:让学生讲述解题路径并说明解题依据;教师要站在变式题组的思维层面,针对学生的吸纳情况给出数学思维渐次攀升的问题).这样的建议虽不中听,但却中肯,也能给参与者提供学科专业发展的指向.

二、考据精神是数学课堂教学应有的精髓

就数学课堂教学而言,记得就是能模仿;晓得就是能理解;明得便是体认了学习对象的本体,亦即对事物本身有了体验.这是三种不同的学习状态,记得不一定晓得,晓得不一定明得,但是明得必定晓得,不必模仿而自然记得.关键是师生都应该有考据的意识,方能让知识因求实而连续、因求证而关联、因求是而完备.这就要求教学问题预设要有空间、问题变式要有契机、思路回流要有时间,方能让数学教学因考据精神的介入而"神清气闲".

1.问题预设要留有考据的空间,知识的连续性因"求实"而记得

案例1:"图形的旋转"性质形成的操作片断.

(1)在平面内,任意给出点A和点O,画出点A绕点O旋转后的对应点;

(2)任意选择一个点B,将其也绕着点O按同样的方式旋转相同的角度,连接AB找出相等的线段和角;

【思考、交流】将线段AB绕点O逆时针旋转60°后的图形该怎么画?

(3)再选择一个点C,你能画出△ABC绕点O按同样的方式旋转同样的角度后的图形吗?找出相等的线段和角.

操作(1)操作(2)操作(3)记录发现

教学分析:教师让学生在操作中发现图形旋转中变与不变的元素(图形旋转不改变图形的形状与大小;图形的位置可能改变,也可能不变,但是图形上的点的位置一定改变),为后续学习圆的旋转不变性奠基.学生经历"3个梯级开放问题+1个闭合思维问题"的思维洗练过程,自然体验到图形旋转的方法就是"将图形的旋转转化为点的旋转",其中旋转中心、旋转角和旋转方向不讲自明;新知在手边诞生并从无序渐次走向有序,终归于理解,获得可理解的图形旋转的本质.这是问题预设留有空间带来的课堂内生成,也是学生求实的考据精神的具象与显化.不过,在知识连续性的层面还是需要一定的思维补位,方能让知识左右勾连,自成一体.

教学建议:散点的知识是不稳定的,很容易被遗忘;唯有站在整体知识的层面,方能让知识根深蒂固.笔者建议采用一副全等的三角板为旋转载体,通过不定式、不定项和不定向的旋转,抽象出图形旋转的本质,进而再借助三角板的立体旋转体验点动成线、线动成面、面动成体的连续性,最终达成内化新知的目标(显性目标,旋转现象→数学化→探索旋转性质;隐性目标,经历分析、概括和抽象的过程,达成三维目标).旋转过程要关注考据精神的融汇,方能让知识因螺旋生成而记得.

2.问题变式要留有考据的契机,知识的关联性因"求证"而晓得

案例2:"图形的旋转"性质的教学片断.

如图1,在6X6的方格纸中,将图形F沿x轴向右平移1格得图形F1,称为作1次P变换;将图形F沿y轴翻折得图形F2,称为作1次Q变换;将图形F绕坐标原点顺时针旋转90°得图形F3,称为作1次Q变换.R″变换表示作n次R变换.

(1)作R4变换相当于至少作_________次Q变换;

(2)请在图2中画出图形F作R2007变换后得到的图形F4.

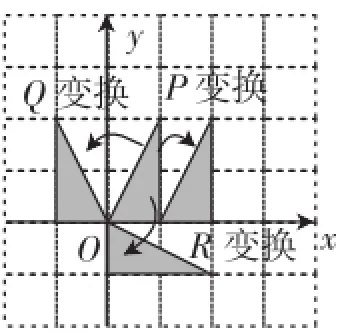
图1

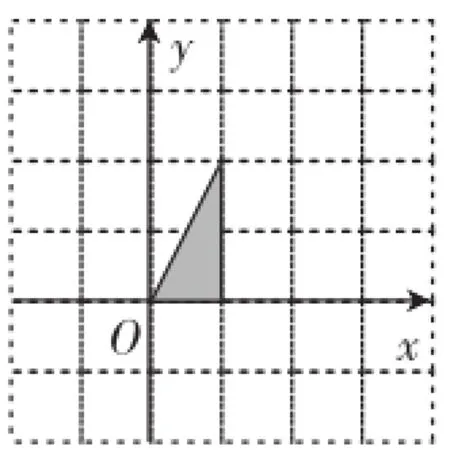
图2

教学分析:原始课堂采用《初中数学伴你学》随堂训练的5个小题(略),试图实现固化旋转图形性质的目标.由于题目本身的思维地位是课前预习身份,因而着力于单个知识散点的罗列,缺乏知识的关联性,固化图形本况且质的功能无法立位和越位.想通过"推演"的方式"激活"孤立的知识点是没有思维的空间和契机的.笔者建议选用案例2呈现的问题情境,能在考据精神的参与下达成关联知识的目标和内化旋转图形的性质之目的.

教学建议:本题是由连云港市中考数学试题改编而来.选用的价值在于这道题将图形的平移、旋转和翻折间的关联性直观呈现,侧重于图形的旋转与图形的翻折(作轴对称)之间关系的显化(作4次R变换相当于作2次R变换).要"求证"图形变换的关联性,没有考据意识的介入是无法获取真知的,让学生在操作中提炼关联性本身就是考据的契机.因此,就这个层面而言,这样的变式载体更具有实现关联的性能,在考据践行中逐步晓得图形旋转的本质和渐次内化图形变换间的关联性.

3.思路回流要留有考据的时间,知识的完备性因"求是"而明得

案例3:"同底数幂的乘法"结课片断.

教学分析:教师让学生自己回流课堂思维,相信学生的思维力量,这种下放"学权"的能力本身就具有一种考据的视野,能给学生的"求是"工作提供客观的思维时空.结课本身就是学生考据行为的过程化,在这一过程中,在逆向思考的帮助下,学生的思维经历元认知域内的"端本澄源"过程,进而获得知识的完备性的理解,这种站在盘点知识的思维经历中获得的知识理解是一种智慧的明得.在具体的结课操作中,执教者是用域内问题引导学生的考据思维的:你从系列运算中发现了什么规律?底数不同的幂相乘能运算吗?如果是三项同底数幂相乘,同底数幂的乘法公式还适用吗?为什么要学习同底数幂的乘法?经历这些问题的思维漂洗,获得完备知识的可信性是可想而知的.但是知识的完备性的获得不仅仅是回流性辨伪就能立竿见影的,还需要关照知识的展延性(学习了同底数幂的乘法运算,还会学习同底数幂的除法运算吗?它们的运算数理一样吗?也能有类似的规律吗?),方能助推知识的完备性并以此明得而迁移.

教学建议:在学生经历去伪存真的考据过程后,明得了新知,为具象知识的纯粹性和完备性储备了基础.笔者认为还要介入章节知识的整体性纲目,让学生获得研究一类问题的方法,让考据行为过程化.因此,还应该追加设问:(1)在已有的知识体系中,你认为哪些知识与本节课的内容通联?连接点在哪儿?(2)你认为我们还应该研究哪些内容?从哪几个方面去研究?为什么要研究?第一个问题能让学生再次链接乘方的意义,使得学习同底数幂的乘法运算在求简层面彰显优势而必要;第二个问题能让学生在考据中伸展研究的视角,使得知识上下贯通、左右联袂而趋于完备.寻求知识完备的过程就是考据行为运行的过程;同时,考据思维追溯的过程又是知识完备不可或缺的契机,渐次完备的知识是容易明得而晓得并记得的.无论考据行为抑或完备知识的求探,这些过程性的思维离不开时间的支持.因此,思路回流要有时间的承载,方能渐次获得完备的知识、方法及经验.

三、一点看法

课堂教学离不开考据行为,因此,教学设计要为考据行为留有余地;教学过程中,学生的考据精神能让"会一题→通一类→连一片"成为可能,教师的考据行为能让"去芜存菁"的思维行为掷地有声.评课中的考据精神是对执教者的尊重和理解,这和裴光亚先生的"为执教者的教学设计进行辩护"的核心精髓是一脉相通的.笔者一直认为,无论学生的思维现状如何,慢理念永远是数学课堂的底蕴,考据精神永远占据数学课堂的核心地位,人文价值是数学课堂亘古不变的本真夙愿.

1.郭康松,胡继芳.论清代数学考据方法[J].湖北大学学报(哲学社会科学版),1999(6).

2.张奠宙.关于数学史和数学文化[J].高等数学研究,2008(1).

3.钱云祥.课堂观察:教学评价的基本路径---例说评课值得关注的几个要素[J].中学数学(下),2015(11).