把数学史料融入数学探究之中

邵汉民 陈芳

【摘 要】“圆周率”是小学阶段一个学生不可能依靠自主探究得到的概念。在对“圆周率”数学史料进行分析的基础上，进行教学构思，首先解决圆周长问题时，设计疑问；接着在实验验证的过程中，进一步积累疑问；然后通过简要回顾数学“圆周率”的历史，认识圆周率；最后总结圆周长公式。

【关键词】圆周率 设疑 积疑 释疑

数学的概念、定义、法则的产生与形成，大多经历了漫长的历程，在课堂上让学生真实地经历这样一个过程，是不可能也是没有必要的。在设计数学探究的过程时，我们通过阅读相关的数学史料，再结合学生的学习现实，确定哪些过程适合于学生探究，哪些过程只要学生读史了解？下面以“圆周长”一课中设计“圆周率的教学”为例来阐述具体做法。

一、读史感悟

圆周长的精确测量是一个千古难题，在对这个难题的破解中，人们发现了圆周率。圆周率的发现经历了实验时期、几何法时期、分析法时期、计算机时期这四个时期。从实验时期到几何时期，是人类对于圆周率求值过程的第一次飞跃，体现了数形结合的思想；从几何时期到分析时期，是代数思想发展带给数学的生机；从分析时期到计算机时期，对圆周率的认识达到了质的飞跃，成为现代计算机技术对数学的一大贡献。

当然，要在短短的40分钟内让小学六年级的学生亲身探究这样的一个过程，无论从时间与已有的知识基础来说是做不到的。我们可以做的是，创设情境，在经历了用实验法只能得到圆周率的大致值的体验之后，介绍之后的关于圆周率的研究成果与方法。在这样一个大的背景下来认识圆周率，学生头脑中的“圆周率”才是比较完整的、真实的。

为得出圆周率，以下两个活动必不可少。

第一，让学生动手量一量圆的周长与直径，再算出它的周长与直径的倍数。

第二，在操作后发现它的结果是三倍多一些，但又不能确定是几时，展示事先准备的资料，介绍圆周率的发现史，进而总结出圆周长的计算公式。

认知心理学认为，人的学习过程是从心理平衡到不平衡再到平衡的一个认知过程。为让学生在圆的周长的教学过程中经历这样一个过程，我们在圆周率的教学这一个环节中设计了积疑、设疑和释疑这样一个学习过程。积疑，就是让学生在直接测量一些圆形物品周长的基础上，指出如果要测量黑板上的圆，怎么办？有没有更好的办法？设疑，就是让学生回顾已有知识，说一说圆的周长与直径之间的倍数关系，了解不同时期对圆周率有不同的说法，并通过实际测量发现，圆周率总是得不到统一。这时教师介绍圆周率的发现史，进行释疑。

二、教学实践

（一）积疑——从可以直接测量圆周长到不可能直接测量

【片段一】

圆的周长与直径的关系是客观存在着的一种现实，对于这一个关系进行探究的目的应该是为了解决实际问题，即当不能直接测量出圆的周长时，怎么办？

教师为同桌学生提供一枚1元硬币与一颗中国象棋子，引导学生“化曲为直”直接测量出圆的周长。接着教师提问，如果要知道画在黑板上的圆周长，你能用什么办法？

师：当一个圆形在某一个柱体上时，可以用化曲为直的方法来解决。但如果是一个圆形，我们直接测量周长就很困难了。你有什么办法来解决这个难题？

生：可以测出圆的直径，再乘3.14。

师：为什么可以这么做？

生：因为圆的周长是直径的3.14倍。（教师板书：“直径 3.14倍”“圆周长=直径×3.14”）

师：你是怎么知道周长是直径的3.14倍的。

生：我是看书知道的。

师：老师也看到一本书，上面是这样介绍的：

公元前200年《周髀算经》 周三径一

生：这里说的是“周长是直径的3倍”。（教师板书：“3倍”）

师：现在怎样求圆周长？

生：圆周长=直径×3。

师：现在我们得到了两个求圆周长的式子，用哪一个来做才是正确的呢，或者说两个都有问题？你有什么办法可以来验证？

（教学意图：对于圆周率的值，有部分学生可能已经通过看书有了认识，但又不可能对其进行全面的了解，教师充分利用学生的这一个认识起点，让学生说一说、算一算。同时教师再举一个书本中的例子，发现书本对于圆周率并没有一个统一的说法。从而产生了一个新的疑问，生发了进一步进行验证的需要。）

（二）设疑——从不能直接测量到探究圆周长与直径的关系求圆周长

【片段二】

用实际测量圆的周长与直径，再通过计算来探究圆周率的过程，就是实验法。这是人类探究圆周率最原始的方法，需要的数学基础知识最少，适合于小学生操作实验。但我们又应该清醒地认识到，这种方法并不是求圆周率的最佳策略，不可能对前面所积累的疑问得到圆满的解决，只是让学生掉进更大的疑问之中。

生：我们前面已经测量出一枚1元硬币和一颗中国象棋圆面的周长，现在只要再测量出它们的直径，除一除就可以得到结果了。

师：听清他讲的意思了吗？（学生测量并计算）

师（找两张结果都是三倍多一点的在投影上展示）：你有什么发现与疑问？

生：我发现求出的结果并不是三倍，而是三倍多一点，而且两次的结果并不相同？

师：有没有结果刚好是3.14的？

有一组学生举手。教师把他们的结果展示出来，见下表。

师：请同学们帮助算一算它的结果。

学生计算后都发现没有计算错误。这时教师追问：你对这组数据有什么疑问？

有些学生思考后举手说：周长这个数据不可能量得这么精确。

师：大家认为呢？（这时学生也恍然大悟）

师：对了，用我们的尺子来量，最多只能精确到十分位。并且用尺子测量线段时，有一些线段是不可能测到它的准确值，这一点到我们读初中时数学老师会给同学们说明。不巧的是，在圆中，直径与周长中至少有一个值是无法用尺子测量到它的准确值的。所以用测量的方法要得到圆周长与直径的倍数的准确值是不可能的。

[教学意图：从圆周率值的精确过程来看，经历了实验法计算时期、几何法计算时期、分析法计算时期与计算机计算时期。学生动手测量只是最为原始的实验法计算时期。因此，在一般情况下是不可能得到如3.14这样的结论的。但学生又是在知道圆周率的值（约）是3.14的情况下进行的，因此就会出现“3.14”这样的值。教师很好地利用课堂的生成资源，组织学生进行讨论，让学生发现其中的不可能处，进一步反证了圆周率并不是正好是3.14。也进一步激发起学生进一步认识圆周率的需要。]

（三）释疑——从得不到一个明确的结论到了解圆周率的认识史

在数学史上，很多数学问题的解决不是一蹴而就的，有一些是通过几十年、几百年甚至几千年的长期努力才获得的。让学生了解圆周率的探究过程，有利于学生更加深刻地理解圆周率。

【片段三】正六边形的研究

教师出示一个圆，再在这个圆内做出一个正六边形。

师：你能说一说正六边形的周长与圆周长的关系吗？

教师再画上正六边形的三条对角线，说一说分别是圆的什么。它的长度相当于几条六边形的边长，那么正六边形的周长是直径的多少倍，也就是周三径一。这个“周”是谁的“周”？（生：正六边形的周长）

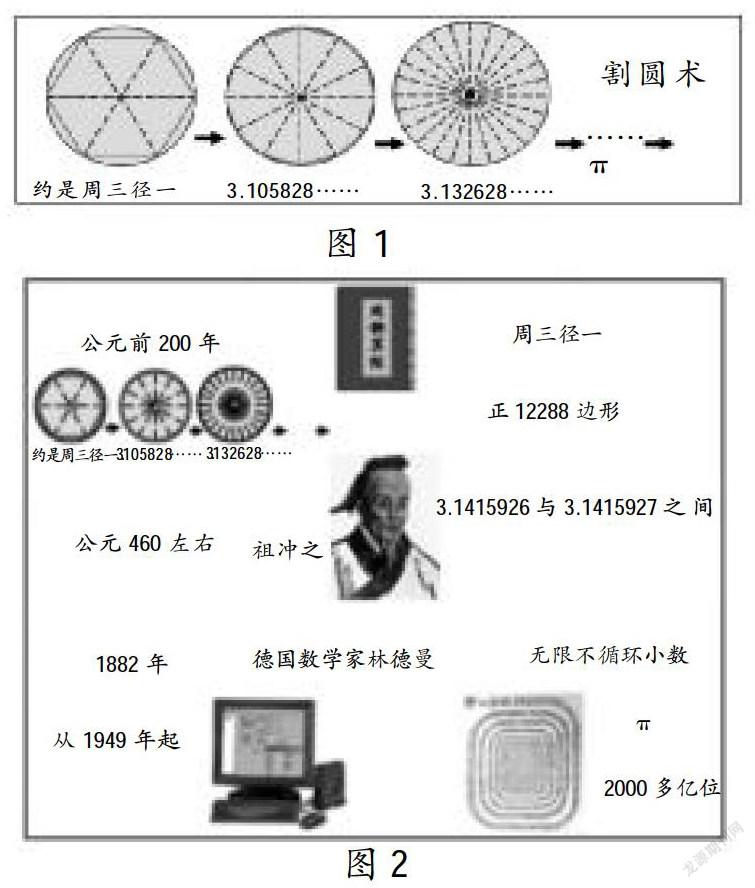
师：那么圆的周长应该是直径的3倍要——（生：多一些），或者说是约是周三径一（教师在“周三径一”的前面加上“约是”）。受到这个图的启发，当时的数学家把这个圆继续分割成——（演示：把圆十二等分后得到的正十二边形 ）。这时的正十二边形的周长和正六边形的周长谁的周长更接近于圆的周长？数学家计算出正十二边形的周长再除以圆的直径得到值为——大屏幕演示。再把刚才的圆二十四等分，得到正二十四边形，计算出近似值是——（大屏幕演示）。你发现这些数值有什么变化规律？这就是有名的割圆术。（多媒体演示见图1）

数学家用这种方法割啊割，“割”了整整六百多年，到了公元460年左右，有一位数学家叫祖冲之，它把圆分割成12288份，得到正12288边形，得到圆的周长是直径的倍数在3.1415926与3.1415927之间。这个发现比国外的数学家早了1000多年。因此人们把这个倍数关系称为“祖率”。

现在你发现前面我们说的3.14倍与3倍是一个什么数？是一个近似数。（教师在前面板书的数据前加上了约等号）1882年，离现在一百多年前的德国数学家林德曼证明了圆的周长与直径的倍数是一个无限不循环小数。这个倍数称为圆周率，为了更好地表示它，数学家用希腊字母“π”来表示，当人类发明了计算机之后，计算这个圆周率就变得轻松了，已经计算到小数点后2000亿位了。出示图形，请学生读一读。教师说明这里还只是表示了圆周率小数点后的前707位。（多媒体演示见图2）

（教学意图：可以这么说，在数学世界中，可能找不到一个数值，像圆周率这样吸引这么多数学家进行这么长时间的研究。因此，让小学生通过实验的方法来明白圆周率的内涵是不可能，如何让学生了解圆周率的历史，教师选取了数学史中的几个典型的片断，让学生“思接千年，情寄数学”。）

（四）反思——从“再计算”的过程中提炼出圆周长公式

【片段四】

师：根据我们这么一段时间的学习，对前面的两个答案有什么进一步的认识？

生：这两个算式中的“3”与“3.14”分别是圆周率的近似值。

师：哪一个值更接近于圆周长的实际值？

师：如果要更精确，可以怎么做？

生：把圆周率的值保留更多的（小数）位数。

师：那么怎样表示出这个周长的精确值？

学生感到疑惑，教师板书40π厘米。说一说为什么这个值是一个精确的值。

生：40是一个一定的数，π也是一个一定的数。

师：现在你能总结出求圆周长的计算公式吗？

生：圆周长=直径×圆周率。

生：C=πd。

（教学意图：明白了圆周率的意义，总结出求圆周长的计算公式，已经不是什么难事了。教师通过与课始的学习材料进行呼应，让学生感受到数学学习与提炼的重要性。）

圆周率的认识与定值过程，是人类对数学的认识与发展的具体表现。教师只有站在文化传承的角度，让学生经历与回顾圆周率的认识的多个历史瞬间，才能感受到数学的内在魅力。

（浙江省杭州市萧山区所前二小 311200浙江省杭州市萧山区湘师附小 311200）