π传奇
徐波
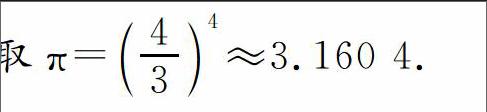


圆周率π就是一个传奇,
一、光辉岁月
古人曾认为圆周率是一个常数,《几何原本》中就提到圆周率是常数,中国古算书《周髀算经》中也说“径一而周三”,认为圆周率是常数,
早期圆周率大多是通过实验而得到的结果,古巴比伦石匾上就清楚地记载过圆周率是25/8,而古埃及纸草书中,取
第一个用科学方法寻求圆周率数值的人是阿基米德,他用圆内接和外切正多边形的周长确定圆周长的上下界,从正六边形开始计算到正96边形,得出圆周率的下界和上界分别为223/71和22/7等,公元263年,中国数学家刘徽在《九章算术》中用“割圆术”计算圆周率,“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣,”这其中的妙处就在于这个算法中已经包含了求极限的思想,公元480年,南北朝数学家祖冲之在前人成就的基础上,得出了π分数形式的近似值,取等为约率,取355/113为密率。
小伙伴们或许听说过,电子计算机的出现使7c值计算有了突飞猛进的发展,1949年美国首次用计算机(ENIAC)计算7c值,一下子就算到小数点后2037位。1989年美国哥伦比亚大学研究人员用计算机算到π值小数点后4.8亿位,后又继续算到小数点后10.1亿位,创下新的纪录,
纵观古今,把圆周率的数值算得这么精确,其实实际意义并不大,现代科技领域使用的圆周率值,有十几位已经足够了,我们计算圆周率,另一个功能是要探究圆周率是否为循环小数,自从1761年兰伯特证明了圆周率是无理数,1882年林德曼证明了圆周率是超越数后,才彻底否定了困惑人们两千多年的“化圆为方”尺规作图问题。
二、神奇应用
π在许多领域都有非常重要而独特的作用,它的性质探讨也吸引了众多数学家,π是个无理数,即不可表达成两个整数之比,但数学中许多恒等式里都有π的参与。如,

