经历过程 发展思维

何萍

[摘 要] 2015年10月，浙江省温州市开展了每年一次的初三教学研讨会. 本次研讨会主要研讨单元复习课教学如何梳理知识，巩固提升，从而发展学生的思维. 现以一节“二次函数复习”为例，与同仁交流.

[关键词] 思维；过程

教学片段呈现

环节1：回顾复习，体验数形结合思想

活动1：已知二次函数y=x2+bx-3的图像经过点A（-1，0）.

（1）这个二次函数的表达式是______；

（2）这个图像的顶点坐标是_____，对称轴为______；

（3）当-1≤x≤0时，y的取值范围为______.

（教师依次呈现（1）、（2）、（3）问，请学生个别回答. 回答第（3）问时，教师进行了提问）

问题1：你是怎么求得y的取值范围的？（学生说代入x的临界值求得）

问题2：y的值会变，那么y的值会怎么变？（启发学生利用函数增减性求解）

（教师将第（3）问进行了变式）

变式：当-1≤x≤4时，y的取值范围为______.

（教师通过下列问题引导学生思考）

问题1：你是怎么求的？（学生说代入x的临界值求得）

问题2：y的值怎么变？（学生画图说明函数增减性）

问题3：你是怎么画出草图的？（复习用五点法画草图）

教师小结：求取值范围，不仅仅代入临界值求值，更要关注函数的增减性，所以，我们解决函数问题时要用好图像这个工具.

环节2：先猜想后验算，感悟数形结合思想

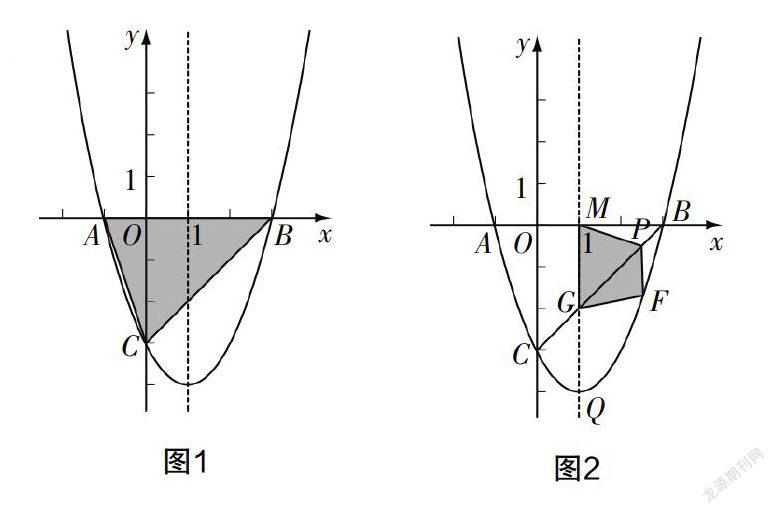
活动2：如图1，抛物线y=x2-2x-3与坐标轴的交点记为A，B，C，连接AB，BC，AC，得到△ABC，在抛物线上再找一点D，使得S=S，则D点的坐标为______.

（教师没有直接让学生求值，而是先提出几个问题引导思考）

问题1：这个D点的位置在哪里？这样的D点你能找到几个？（学生说找到了3个）

问题2：你觉得哪个点的位置最好求？坐标是多少？你是怎么求的？（学生利用同底等高直接求出点C关于对称轴对称的对称点的坐标）

问题3：那么另外两个D点的大概位置在哪儿？（学生画出大致位置）

接着，教师让学生进行求解验证. 在学生求解后，教师引导学生总结出将二次函数问题转化为一元二次方程求解.

环节3：综合运用，应用数形结合思想

活动3：二次函数y=x2-2x-3的图像如图2所示.

（1）P为线段BC上的任意一点，设P点的横坐标为x，请你写出P点的坐标：______.

（2）过P点作x轴的垂线与抛物线交于点F，是否存在点F，使得线段PF的长度有最大值？若存在，求出线段PF的长；若不存在，请说明理由.

（3）M是对称轴与x轴的交点，G是对称轴与线段BC的交点，在线段BC上是否存在一点P，使得四边形MGFP是平行四边形？若存在，求出此时P点的坐标；若不存在，请说明理由.

（教师先呈现（1）问，在学生解决（1）问后归纳）

教师归纳：P是线段BC上的一个动点，所以它的横、纵坐标都是变量，但不管怎么变，它们始终有不变的关系，那就是y=x-3.

（在呈现（2）问之前，教师先引导学生观察图形）

问题1：点P从B到C的过程中，PF的长度怎么变？（引导学生观察图形PF的变化）

问题2：什么时候PF最大？（引发学生观察图形猜想，有学生猜想PF与GQ重合时PF最大，也有学生猜想在x=时PF最大）

教师接着呈现（2）问，让学生求解验证猜想.

（解决（2）问之后，在呈现（3）问之前，教师以下列问题继续引导学生观察图形）

问题1：连接M，G，F，P，在点P从B到C的过程中，四边形MGFP的形状会发生变化吗？

问题2：有没有可能是特殊四边形？如果有，是什么图形？

问题3：四边形MGFP什么时候是平行四边形？你是怎么判断的？（学生回答当PF=MG时）

问题4：观察图形，P从B到C的过程中，由于PF的长度变化是从小到大再到小，此时有几种PF=MG的情况？（继续引导学生根据点的运动来想象图形）

学生画出两个可能的平行四边形，教师继续追问.

问题5：你是怎么画出这两种情况的？（启发学生从PF最大值的角度观察PF的左右两边出现PF=MG的情况）

问题6：点P从B点运动到C点的过程中，始终有PF∥MG，那么在PF∥MG条件下，你还有其他方法判定四边形MGFP是平行四边形吗？（激发学生思维，复习回忆平行四边形的判定）

问题7：PF=MG和MP∥GF，你觉得你能求哪个？（学生回答目前能求PF=MG）

接着教师呈现（3）问让学生求解验证，并对（3）问进行追问.

问题8：如果P点沿着射线BC继续运动，还能得到以M，G，F，P为顶点的平行四边形吗？什么时候是平行四边形？（继续引导学生画出图形）

接着，教师呈现问题变式，让学生求解.

变式：在射线BC上是否存在一点P，使得以M，G，F，P为顶点的四边形是平行四边形？若存在，求出此时P点的坐标；若不存在，请说明理由.

环节4：概括小结，提炼函数思想

教师呈现本节课的复习框图（图3），总结：解决动点问题时，首先观察图形的变化，如果需要确定图形变量之间的关系时，通常建立函数模型求解；如果已经确定了图形之间的特殊位置或者一些特殊值时，可以建立方程模型求解. 其中，变量的对应关系是函数知识的核心，我们在解决函数问题时，要学会观察图形的变化，关注变量的变化规律，这是解决问题的关键.

单元复习课的视角在哪儿

单元复习课是以复习巩固某一单元知识为主要任务的一种数学课型. 通过单元复习，使得学生对知识建立结构化、网络化和关系化，又通过查漏补缺，提升学生的数学学习能力. 所以，单元复习课要把学生摆在主体地位，给学生以充分的思考空间，让学生参与数学问题解决的全过程，建立平等、和谐的课堂气氛. 单元复习课的目标视角不宜过大，应注重核心问题、课标要求.

1. 课标的视角：重视过程体验和数学活动经验的积累

《课标》（2011年版）指出：“学生学习应当是一个生动活泼的、主动的和富有个性的过程……学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程……使学生体会和运用数学思想与方法，获得基本的数学活动经验. ”抓住“过程教学”和“数学活动经验积累”，让单元复习课摆脱“题海战术”的旧模式，上出新意.

本节课围绕着一条抛物线y=x2-2x-3，让学生充分经历了二次函数的概念、图像、性质等基础知识的复习过程；让学生经历“想图形、画图形、算图形”的全过程，层层递进，促进思考自变量在不同取值范围下的函数增减性，体验“形”的重要性；借助故事叙述的方式引导学生去发现由动点引起图形变化的过程，激发学生先猜想，再求解验证的思考过程，并通过自己的思考积累思维活动经验，从而掌握解决动点问题的一般方法.

数学活动经验的积累是提高学生数学素养的重要标志. “数学活动经验”是在“做”中积累起来的. 教师要设计有效的数学活动，深化学生对数学的理解，对数学在实际中应用的理解.

2. 系统的视角：抓住数学的核心概念和思想方法

章建跃教授指出：“构建反映数学内在发展逻辑、符合学生数学认知规律的中学数学核心概念、思想方法结构体系，并使核心概念、思想方法在数学课堂中得到落实，是提高数学课堂教学质量和效益的突破口，同时也是数学课堂教学改革的抓手. ”单元复习课也要站在系统的角度，重新审视核心知识的地位和作用，主动构架，提高单元复习课的效率.

纵观中学数学教材，二次函数占有极为重要的地位. 其中，有关二次函数的概念、图像、性质和应用的讨论和研究是相当充分的. 本例中，选取动点为载体，围绕着二次函数的核心知识和动点问题展开教学，注重图像在解决问题中的辅助作用，既使学生所学的分散知识系统化，又让学生在经历问题解决的过程中体验数形结合思想和函数思想，突出了本章的核心知识和核心思想. 同时，研究函数所提供的动态的方法、数形结合思想有利于拓展学生的思维，促进学生后续学习.

3. 学生的视角：发展思维

从学生的视角来看，提升复习课的思维含量才能让学生动起来，才能激发学生的学习欲望. 单元复习课，应该从关注考试转变到关注学生，注重发展学生的数学思维.

比如，环节2，先让学生猜D点的位置，然后再求解；环节3，由一个点的位置的变化，引起线段长度、图形形状的变化的过程，让学生先通过观察图形猜线段的最大值，猜平行四边形的个数，目的是为了引导学生关注运动趋势去猜测，猜测是为了激发学生的思维，先猜再求解验证，这是动点教学的一般方法. 然后将“点在线段上运动”变化到“点在射线上运动”，继续引导学生进行分类讨论解决问题，体会分类思想. 这样设计，不仅让学生直观感知了数形结合意识，也突出了解决动点问题的一般方法的思考途径，同时在解决问题中，渗透了函数思想和化归思想，有利于培养学生良好的思维习惯，从而发展数学思维.