番木瓜果浆微波辅助泡沫干燥过程中营养成分降解模型

唐　辉,李梦雨,陈文学,胡月英

(1.海南大学食品学院,海南海口　570228;2.海南大学材料与化工学院,海南海口　570228)



番木瓜果浆微波辅助泡沫干燥过程中营养成分降解模型

唐辉1,李梦雨1,陈文学1,胡月英2,*

(1.海南大学食品学院,海南海口570228;2.海南大学材料与化工学院,海南海口570228)

在前期的番木瓜果浆微波辅助泡沫干燥工艺基础之上,探究果浆在微波辅助干燥过程中主要物质的含量变化规律。探究了不同微波功率下水分含量变化规律和营养物质含量变化规律,并对所得的动力学方程进行验证。研究结果表明:在水分含量模型中Page方程模型预测值与实验值拟合度最高,R2为0.9884;在维生素C含量模型中零级反应模型预测值与实验值拟合度最高,R2为0.9702;胡萝卜素含量模型中一级反应动力学模型预测值与实验值拟合度较高,R2为0.9185。以上所得方程模型验证结果表明,模型预测值与实验值差异不显著,模型均能较好的反映木瓜微波辅助泡沫干燥过程中主要物质的动力学特征。

番木瓜果浆,泡沫干燥,微波干燥,干燥模型,模型验证

番木瓜(Carica papaya L),又名“万寿果”、“乳瓜”等,其原产于墨西哥和中美洲,在17世纪传入我国,广泛的种植于广东、海南、广西、云南等地[1-2]。番木瓜营养价值丰富,富含酶类、有机酸类以及各种维生素类,其中含有赖氨酸、缬氨酸、异亮氨酸等17种氨基酸,具有补充营养、增强人体免疫力、清除人体自由基以及抗菌抗病原体等保健作用[2]。目前,在食品行业番木瓜被广泛的应用于饮料、果脯以及发酵工业;在医药行业番木瓜有镇痛去湿等作用;而从番木瓜中提取的凝乳蛋白酶在化妆品行业有增加肌肤弹性和美化肌肤的功效[3]。可见,番木瓜在各个行业下可利用前景广阔。

微波加热具有加热速度快、均匀加热、节能高效、易于控制且低温杀菌、安全无害等作用[4]。与传统的加热方式相比,极大地提高了干制品的质量效果[5],在很高程度上保存了干制品的营养物质。

传统的干燥方法会容易引起果浆中的营养物质的降解,导致产品中营养物质的保留率不高。而泡沫干燥是指通过使物料的内部产生大量的泡沫,增加干燥表面积,从而提高干燥效率,且能最大程度上的保留原料中的营养物质。泡沫干燥适用于含糖量较高、热敏性强的食品物料[6]。郑先哲等研究了微波辅助泡沫干燥树莓果浆的干燥特效以及其中营养成分的降解模型[7],而张宝辉等研究了果浆微波辅助泡沫干燥品质以及对其干燥过程进行了模拟研究[8]。

在水分含量动力学研究方面,张红卫等研究了土壤表层水分含量指数模型,为土壤浅层水分监测奠定了理论基础[9];王强应用了单扩散模型来拟合新鲜无核紫葡萄在自然晾晒、烘箱干燥和热风对流干燥过程中水分含量规律[10];而林向阳等研究了茶叶真空微波干燥规律,并建立了茶叶干燥过程水分含量的单项扩散模型、Page模型以及指数模型,为绿茶的加工生产提供了理论依据[11]。在营养物质含量动力学方面,范新光等应用了零级反应动力学和一级反应动力学模型探究了鲜切西兰花经减压处理后贮藏过程中维生素C的含量变化,由此建立了西兰花的货架期预测模型[12];钟金峰等运用零级动力学模型和一级反应动力学模型拟合了竹笋在不同温度热烫下颜色变化规律[13],为其探究产品护色提供了可靠参数。

本研究以番木瓜泡沫果浆为研究对象,果浆在实验用的微波设备作用下,测定其在作用过程中水分、维生素C以及胡萝卜素的含量,从而探究番木瓜泡沫果浆的水分以及营养成分的含量规律,建立整个干燥过程中的降解模型。同时使用在适宜的微波功率条件下测定的实验数据与模型预测值进行模型验证。

1　材料与方法

1.1材料与仪器

新鲜番木瓜购自海口市南国贸易有限公司;单硬酯酸甘油酯(GMS)、大豆分离蛋白(SPI)上海原叶生物科技有限公司,分析纯;羧甲基纤维素钠(CMC-Na)国药集团化学试剂有限公司,分析纯;维生素C标准品天津市天新精细化工开放中心,分析纯;实验用水,蒸馏水。

NM-GS597M型微波炉上海松下微波炉有限公司;HH.S11-1型数显恒温水浴锅上海博迅有限公司;DHG-9073A型电热恒温鼓风干燥箱上海一恒科学仪器有限公司;TU-181OSPC型紫外可见分光光度计北京普析通用仪器有限责任公司。

1.2实验方法

1.2.1实验设计微波辅助番木瓜泡沫干燥样品制备流程为:

实验样品制备:选取新鲜、成熟度适中的番木瓜清洗,去皮、去籽、去瓤、切块,取100 g番木瓜用打浆机打浆6 min,至果浆均匀且细腻以备用。取6.828%的单甘脂(GMS)与4%的大豆分离蛋白(SPI)溶解于100 mL蒸馏水中,将混合液置于70 ℃条件下水浴30 min并不断搅拌以配制起泡剂。将已配制的起泡剂与番木瓜果浆按体积质量比为1∶1的比例进行混合,将混合果浆搅拌2 min后添加浓度为0.5%的羧甲基纤维素钠溶液20 mL并继续打浆2 min,直至所形成的果浆泡沫均匀。

取60 g的木瓜泡沫果浆,均匀平铺于微波载体中,泡沫果浆的厚度为5 mm。将木瓜泡沫果浆在合适的功率条件下,干燥至干燥终点(达国家标准),测定其干燥过程中的水分、维生素C、以及胡萝卜素的含量。

1.2.2实验指标的测定水分含量的测定采用国标的直接干燥法[14];维生素C的测定方法为紫外分光光度法[15];而胡萝卜素的测定方法为分光光度法[16]。

1.3含量模型

番木瓜泡沫果浆在微波干燥过程中不同的成分含量变化可通过不同的模型进行模拟预测。

1.3.1水分含量模型在微波作用下,物料中的水分在微波热效应的作用下受热蒸发,物料的含水量逐渐减小,直至含水量趋于稳定达到干燥终点。而在干燥过程中水分含量的变化选择采用指数模型、单扩散模型以及Page模型进行模型探究[17-18]。

指数模型为(Lweis;Newton):在牛顿冷却定律基础上建立的一种描述水分子运动的模型。其表达式为:

MR=exp(-kt)

式(1)

单扩散模型(Henderson and Pabis):主要根据Fick第二定律,假设物料中的水分是以液态水的形式从表面向外扩散,在干燥条件一定的情况下,只取扩散方程的前一项,得到单项扩散模型:

MR=A×exp(-kt)

式(2)

Page方程模型:Page方程对指数模型进行了修正,增加了一项参数,得到Page方程:

MR=exp(-ktN)

式(3)

以上三个模型公式中:MR=(M-Me)/(M0-Me),而M为t时刻时物料的干基含水量,M=kg水/kg干物质;Mo指物料原始干基含水量,Mo=kg水/kg干物质;Me指物料质量平衡时的干基含水量,Me=kg水/kg干物质;t指干燥时间(min),而A、k以及N均为待定系数。

由微波对番木瓜泡沫进行干燥,至干燥终点时物料中的平衡含水量不易测定,且数值较小,故忽略不计。则MR=M/Mo

将以上的式(1)、(2)以及(3)进行对数计算可得:

ln(MR)=-kt

式(4)

ln(MR)=ln(A)-kt

式(5)

ln[-ln(MR)]=ln(k)+N×ln(t)

式(6)

在初始装载量以及物料厚度一定的条件下进行干燥,功率有关干燥效果与,可以用微波强度(P)来代替微波功率的变化。根据实验数据,分别作不同功率下的 ln(MR)-t曲线和ln[- ln(MR)]-lnt曲线。

对于指数模型的变换,将式(4)引入待定系数 a、b、c,令:

k=a+bP+cP2

式(7)

将式(7)代入式(4)可得到下列表达式:

ln(MR)=-(a+bP+cP2)×t

式(8)

令y1=-ln(MR),x1=t,x2=P×t,x3=P2×t,则式(8)可化解成:

y1=ax1+bx2+cx3

式(9)

对于单扩散模型的变换,将式(5)引入待定系数a1、b1、c1、d1、e1、f1,令:

k=a1+b1P+c1P2

式(10)

ln A=d1+e1P+f1P2

式(11)

将式(10)、(11)代入式(5)可得到下列表达式:

ln(MR)=(d1+e1P+f1P2)-(a1+b1P+c1P2)t

式(12)

令y2=ln(MR),z1=P,z2=P2,z3=t,z4=Pt,z5=P2t,则式(12)可化解成:

y2=d1+e1z1+f1z2-(a1z3+b1z4+c1z5)

式(13)

而对于Page方程的变换,将式(6)引入待定系数a2、b2、c2、d2、e2、f2、g2、h2、i2和j2,令:

ln k=a2+b2P+c2P2

式(14)

N=d2+e2P+f2P2

式(15)

将式(14)、(5)代入式(6),可得到下列表达式:

ln[-ln(MR)]=(a1+b2P+c2P2)+(d2+e2P+f2P2)lnt

式(16)

令 y3=ln[-ln(MR)],k1=P,k2=P2,k3=lnt,k4=Pln(t),k5=P2lnt,则式(16)可化解成:

y3=a2+b2k1+c2k2+d2k3+e2k4+f2k5

式(17)

则以上式(9)、(13)、(17)分别表示了指数模型、单扩散模型和Page方程的变化模型。

1.3.2物料含量模型(维生素C以及胡萝卜素)在微波泡沫干燥过程中的维生素C和胡萝卜素含量模型,探究了零级反应模型以及一级反应模型[19]:

零级反应数学方程为:

C=Co-kt

式(18)

则:kt=Co-C

式(19)

而设定k=a+bP+cP2

式(20)

则将式(20)带入式(18)可得:

Co-C=(a+bP+cP2)×t

式(21)

令Y1=Co-C,x1=t,x2=Pt,x3=P2t,则式(20)可化解成:

Y1=ax1+bx2+cx3

式(22)

一级反应动力学方程为:

C=C0×exp(-kt)

式(23)

k=a+bP+cP2

式(24)

且令MR=C/C0

将式MR和式(24)代入式(23)可得到下列表达式:

ln(MR)=-(a+bP+cP2)t

式(25)

令Y2=-ln(MR),z1=t,z2=Pt,z3=P2t,则式(25)可化解成:

Y2=az1+bz2+cz3

式(26)

1.4数据统计分析

本实验数据采用SAS软件、Design Expert软件以及Excel数据处理软件进行数据处理,每组实验数据均重复取样3次进行实验,使用平均值。

2　结果与分析

2.1干燥过程中水分变化及模型分析

2.1.1水分含量曲线在微波泡沫干燥过程中,泡沫果浆的水分含量随着干燥时间的增加趋于递减趋势,最终达到干燥终点,物料的含水量达到近乎恒定值[20]。各功率下干燥过程中含水量如图1所示。

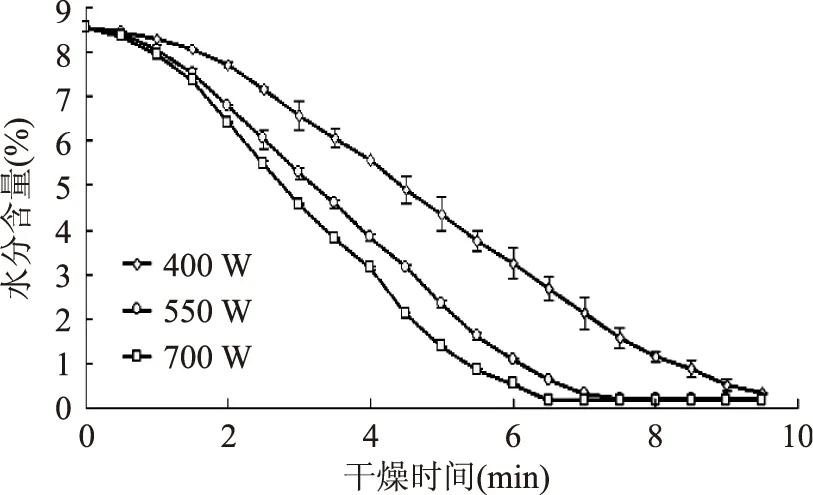
图1　水分含量曲线Fig.1　The curve of the moisture content

由图1中趋势可以看出,番木瓜泡沫果浆的最初含水量为8.54%,在400 W的功率条件下需干燥9.5 min;550 W时需干燥8 min干燥;而700 W条件下只需干燥6.5 min。微波功率越大,有益于物料内部热量的增加,干燥速率越快,且得到的最终干燥产物的含水量越低。由此可见微波功率对番木瓜泡沫干燥成品的质量影响极大。

2.1.2水分含量模型分析探究在400、550 W以及700 W功率下,作用于厚度为5 mm而质量为60 g的番木瓜泡沫果浆微波辅助干燥过程水分含量的模型。利用SAS9.1统计软件实验数据进行多元线性回归分析[21]。由实验数据可得出ln(MR)-t以及ln(-ln(MR))-ln t的关系,如图2、图3所示。

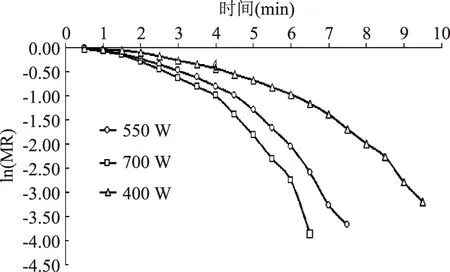
图2　不同微波强度下的ln(MR)-t曲线Fig.2　The curve of ln(MR)-t underthe different microwave intensity

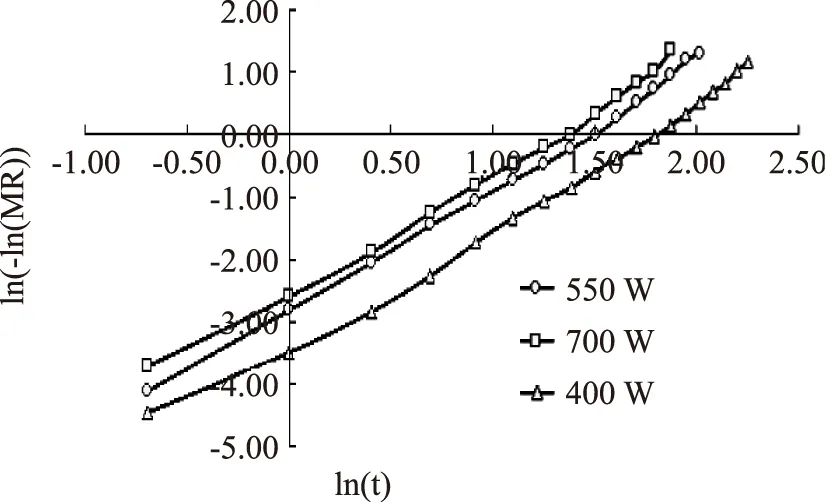
图3　不同微波强度下的ln[-ln(MR)]-ln(t)曲线Fig.3　The curve of ln[-ln(MR)]-ln(t)under the different microwave intensity

由图2、图3可以看出ln(MR)与时间t之间的线性关系不明显,而ln(-ln(MR))与ln(t)之间的线性关系比较明显。

由三个功率下的测试结果可求得上式(9)、式(13)和式(17)的各待定系数以及各方程的方差分析,分析结果如表1所示。

由表1可以看出,指数模型回归方程显著水平p<0.0001,则X2对y1有显著性影响;而单扩散模型回归方程的Z1、Z4对y2有显著性影响;在Page方程中K1、K2、K3、K4、K5对y3有显著影响。将以上各模型的系数值带入式(9)、式(13)、以及式(17)中,可得到以下方程:

ln(MR)=-0.03527Pt

式(27)

ln(MR)=0.07522P+0.04956Pt

式(28)

ln[-ln(MR)]=(-0.85487P+0.055494P2)+(-2.27216+0.96382P-0.052192P2)ln(t)

式(29)

表1　指数模型、单扩散模型以及Page模型回归系数表

由于以上模型回归方程均表现为极显著,所以对其进行相关系数的拟合程度以及比较模型间的优劣以此对其进行综合分析,分析结果如表2所示。

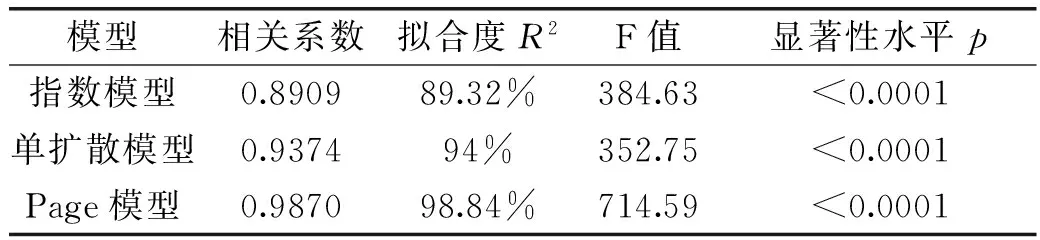
表2　指数模型、单扩散模型以及Page模型统计分析表

由表2可知,指数模型、单扩散模型和Page方程的F值分别为384.63、352.75和714.59,而显著性水平p<0.0001,由此可见三个模型的回归方程均极显著。相关系数表现了实验数据与预测数据之间的拟合关系。一般而言,相关系数越大,则说明模型与实验数据拟合程度越高。表2中,指数模型、单扩散模型和Page模型的相关系数分别为0.8909、0.9374和0.9870,可以得出Page模型的相关系数高于指数模型和单扩散模型,而Page模型的拟合度为98.40%也高于指数模型和单扩散模型的89.32%和94%,所以Page方程对实验数据的拟合效果很好。说明三个模型中Page模型能够更好的描述木瓜果浆微波泡沫干燥特性。而根据所得相关系数可得Page模型方程为:

式(30)

2.2干燥过程中维生素C降解及模型分析

在微波辅助泡沫干燥过程中,维生素C发生了部分降解,导致在干燥制品中,维生素C的含量有所下降[22]。而通过对其降解过程进行分析以及模型设计,能够有助于对干燥过程中维生素C含量的变化规律进行预测。

按照1.3.1工艺参数进行干燥,每1min测定一次维生素C的含量。根据数据得到不同初始微波强度下Co-C-t(零级反应)曲线以及-ln(MR)-t(一级反应)曲线,曲线如图4、图5。

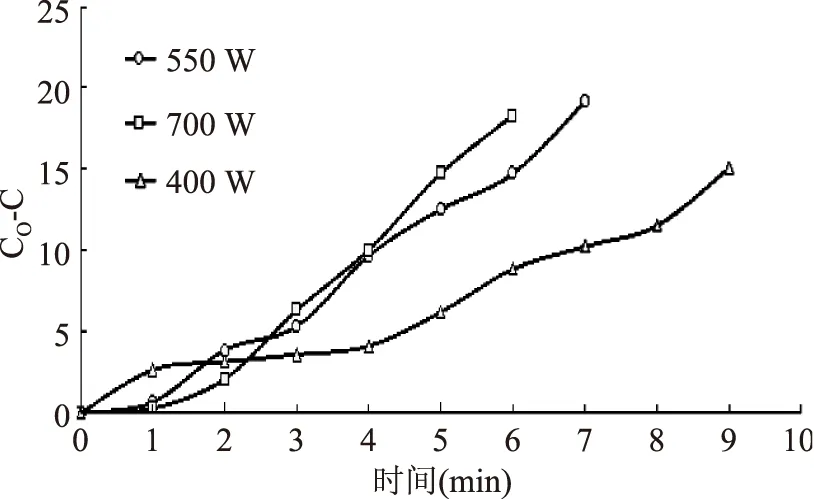
图4　不同微波强度下的Co-C-t曲线(零级反应)Fig.4　The curve of Co-C-tunder the different microwave intensity(zero order model)

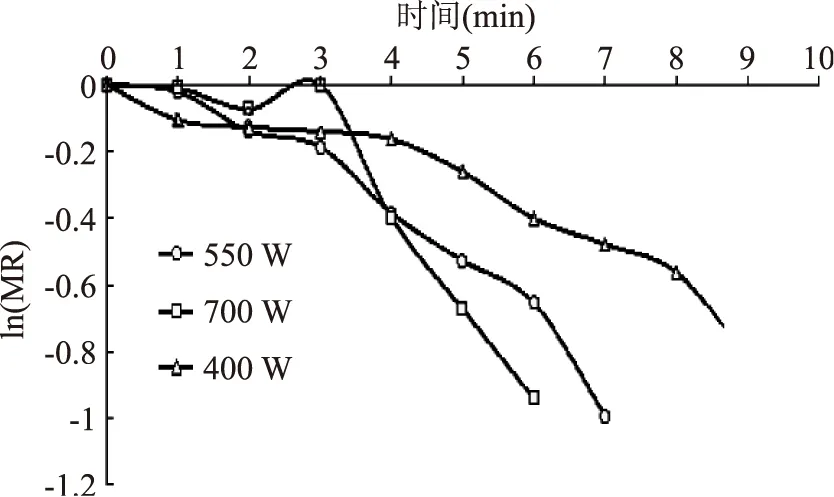
图5　不同微波强度下的-ln(MR)-t曲线(一级反应)Fig.5　The curve of-ln(MR)-t underthe different microwave intensity(first order reaction kinetics)

由图4、图5可以看出,Co-C-t(零级反应)比-ln(MR)-t(一级反应)具有更加明显的线性关系。则利用SAS9.1对实验数据进行多元线性回归分析,由测试结果求得零级反应的式(21)和一级反应的式(25)的各项待定系数以及对方程进行方法分析,所得结果如表3所示。

由表3各方程的回归系数和各回归系数的显著水平可知,对于零级模型,回归方程的 x2对 Y1有显著影响;而一级模型,回归方程的z2对Y2有显著影响。将各系数代入式(21)和式(25)中,分别得到:

Co-C=0.2411Pt

式(31)

-ln(MR)=0.0113Pt

式(32)

由于两种模型的回归方程均极显著,则采用相关系数的拟合程度,比较不同模型间的优劣。两种模型的综合分析比较如表4所示。

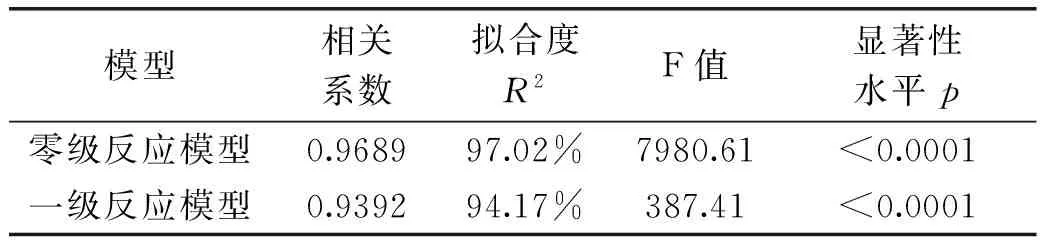
表4　零级模型、一级模型统计分析表

由表4可知,零级反应模型和一级反应模型的F值分别为7980.61和387.41,p<0.0001,两个模型的回归方程均极显著。而根据相关系数表现实验数据与预测数据间的关系,一般而言,相关系数值越大,说明模型与数据拟合得越好。表4中,零级反应模型和一级反应模型的相关系数分别为0.9689和0.9392,可以看出零级反应模型的相关系数高于一级反应模型,零级反应模型的拟合度为97.02%也较高于一级反应模型,对实验数据的拟合效果很好。说明两个模型中零级反应模型能更好的描述木瓜果浆微波泡沫干燥特性。因此,番木瓜果浆微波辅助泡沫干燥过程中维生素C含量的数学模型为:

c=c0-0.2411×p×t

式(33)

2.3干燥过程中胡萝卜素降解及模型分析

在微波辅助干燥番木瓜泡沫果浆的过程中,果浆中的胡萝卜素发生了降解,物料中总的胡萝卜素的含量降低[23]。通过对其降解过程进行分析以及模型设计,能够有助于对干燥过程中胡萝卜素含量的变化规律进行预测。

按照1.3.1相同工艺参数,每1 min测定一次胡萝卜素含量。根据测定的数据得到不同初始微波强度下Co-C-t(零级反应)曲线以及-ln(MR)-t(一级反应)曲线,曲线如图6、图7所示。

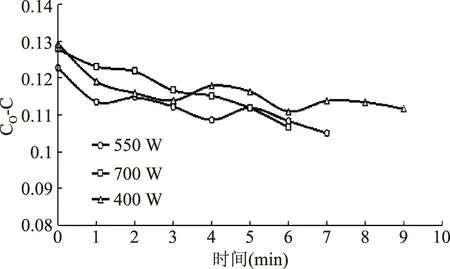
图6　不同微波强度下的Co-C-t曲线Fig.6　The curve of Co-C-tunder the different microwave intensity

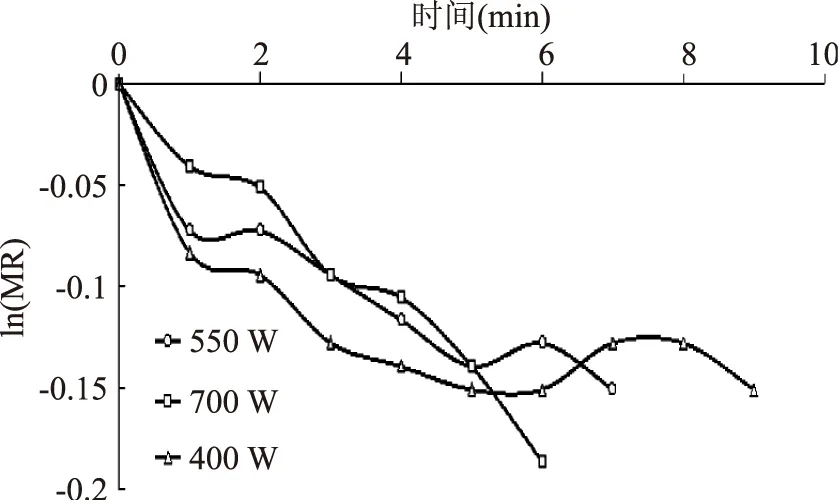
图7　不同微波强度下的-ln(MR)-t曲线Fig.7　The curve of-ln(MR)-tunder the different microwave intensity

由图6、图7可以看出,在Co-C-t(零级反应)曲线与-ln(MR)-t(一级反应)曲线中,Co-C-t(零级反应)曲线比-ln(MR)-t(一级反应)曲线表现出更加显著的线性关系。则使用SAS软件对数据进行多元线性回归分析,由550 W条件下的测试结果求得式(21)、(25)的各个待定系数以及方程的方差分析数值,得到回归系数表如表5所示。

由表5可知,对于零级反应模型,回归方程的x2对Y1有显著影响,p<0.0001;对于一级反应模型,回归方程的z2对Y2有显著影响。将各系数带入式子(21)、(25)可得:

Co-C=0.000138Pt

式(34)

-ln(MR)=0.00270Pt

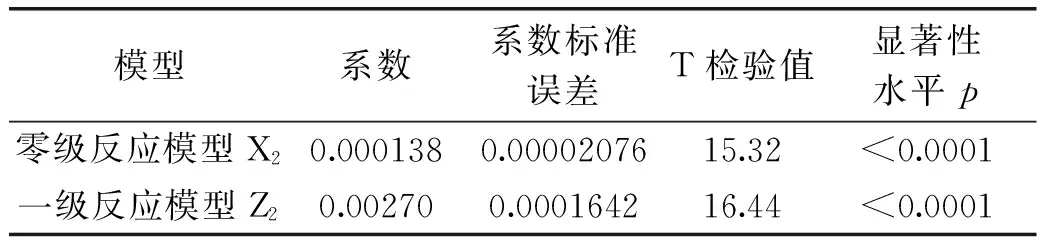
式(35)

由于两种模型的回归方程均极显著,采用相关系数的拟合程度,比较不同模型间的优劣。得到的相关系数等值如表6所示。

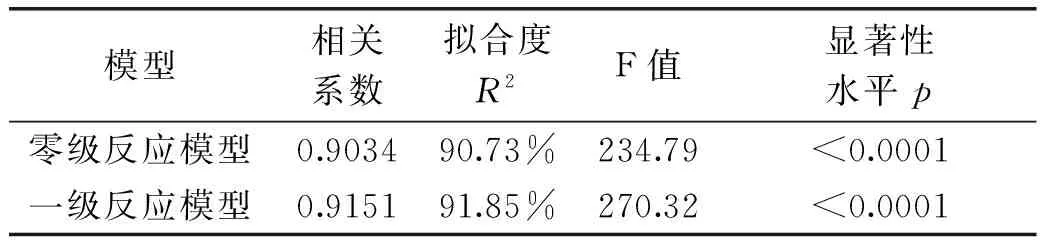
表6　零级模型、一级模型统计分析表

由表6可以看出,零级反应模型和一级反应模型的F值分别为234.79和270.32,p<0.0001,两个模型的回归方程均极显著。

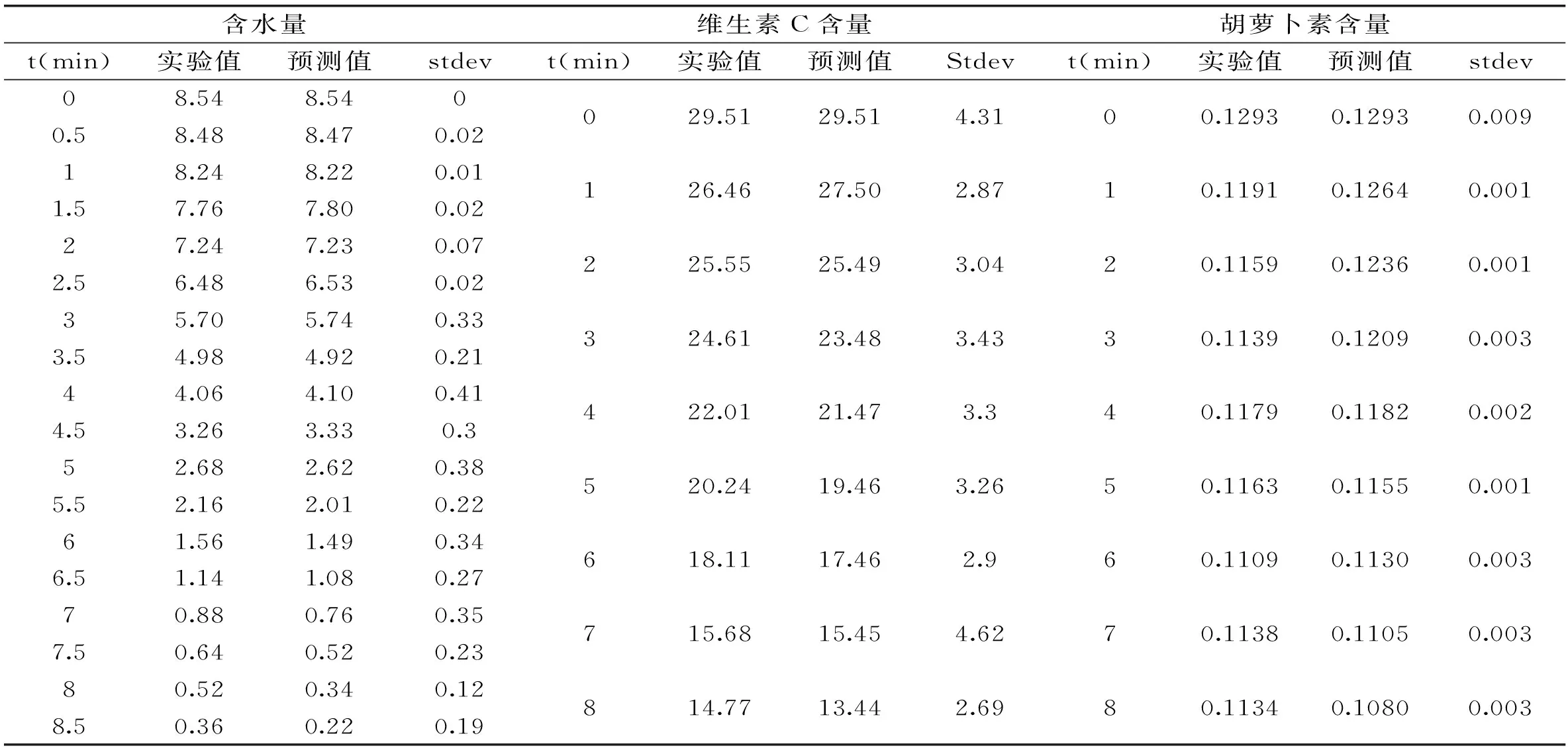
表7　500 W条件下实验值与模型预测值记录表

而相关系数表现实验数据与预测数据间的关系,且值越大说明模型与数据拟合得越好,则一级反应模型比零级反应模型能够更好的与数据拟合。并且一级反应模型的拟合度为91.85%高于零级模型的90.73%,所以两个模型中一级反应模型能更好的描述木瓜果浆微波辅助泡沫干燥过程中胡萝卜素的含量规律,则对应的一级反应动力学模型为:

C=C0×λ(-0.0027pt)

式(36)

3　模型验证

番木瓜果浆微波辅助泡沫干燥,当所使用的微波功率为100 W时,物料的干燥速度过慢;而当所使用的微波功率为1000 W时,物料的干燥速度由过快,容易引起物料的焦化[24]。所以在进行验证实验时我们采用500 W和600 W作为功率条件对水分含量的Page模型;维生素C含量的零级反应模型以及胡萝卜素含量的一级反应模型进行验证实验。

在500 W的干燥条件下,每30 s测定一次含水量,每1 min测定一次维生素C含量以及胡萝卜素的含量。以干燥功率和干燥时间为已知条件,通过Page模型、零级反应模型以及一级反应模型进行预测对应干燥时间的含水量、维生素C含量以及胡萝卜素的含量,将所得结果如表7所示。

由表7所得的实验值、预测值根据t值检验法对其数据差异显著性进行检验:对于400W条件下Page模型所得预测值与实验值进行检验得到t=0.0139,而t理论值为1.740,则可得t0.05,则模型所得预测值与实验值差异不显著;根据相同的方法对维生素C含量零级模型以及胡萝卜素含量一级反应模型进行验证,验证结果为零级模型的预测值与实验值差异不显著,一级模型的预测值与实验值差异不显著。验证结果说明实验所得模型预测值与实际干燥过程中实验值基本吻合,以上三个模型可较准确的预测该功率条件下干燥过程中水分、维生素C以及胡萝卜素的含量。

在600 W的干燥条件下,由于微波强度的提高,使得干燥效率的提高,则干燥时间降低,每30 s测定一次含水量,每1 min测定一次维生素C和胡萝卜素含量。以干燥功率和干燥时间为已知条件,通过Page模型、零级反应模型以及一级反应模型进行预测对应干燥时间的含水量、维生素C含量以及胡萝卜素的含量,将所得结果如表8所示。

对表8数据进行验证分析,使用t值检验法对其数据显著性进行检验:600 W条件下水分含量模型Page方程的所得预测值与实验值进行检验得到t0.05则所得预测值与实验值差异不显著,说明Page方程模型可以较准确的预测干燥过程中水分含量的变化。同理对维生素C含量的零级方程以及胡萝卜素的一级反应方程进行t值检验,验证结果为实验值与预测值均表现为差异不显著,说明所得模型可很好的描述在干燥过程中水分、维生素C以及胡萝卜素含量的变化。

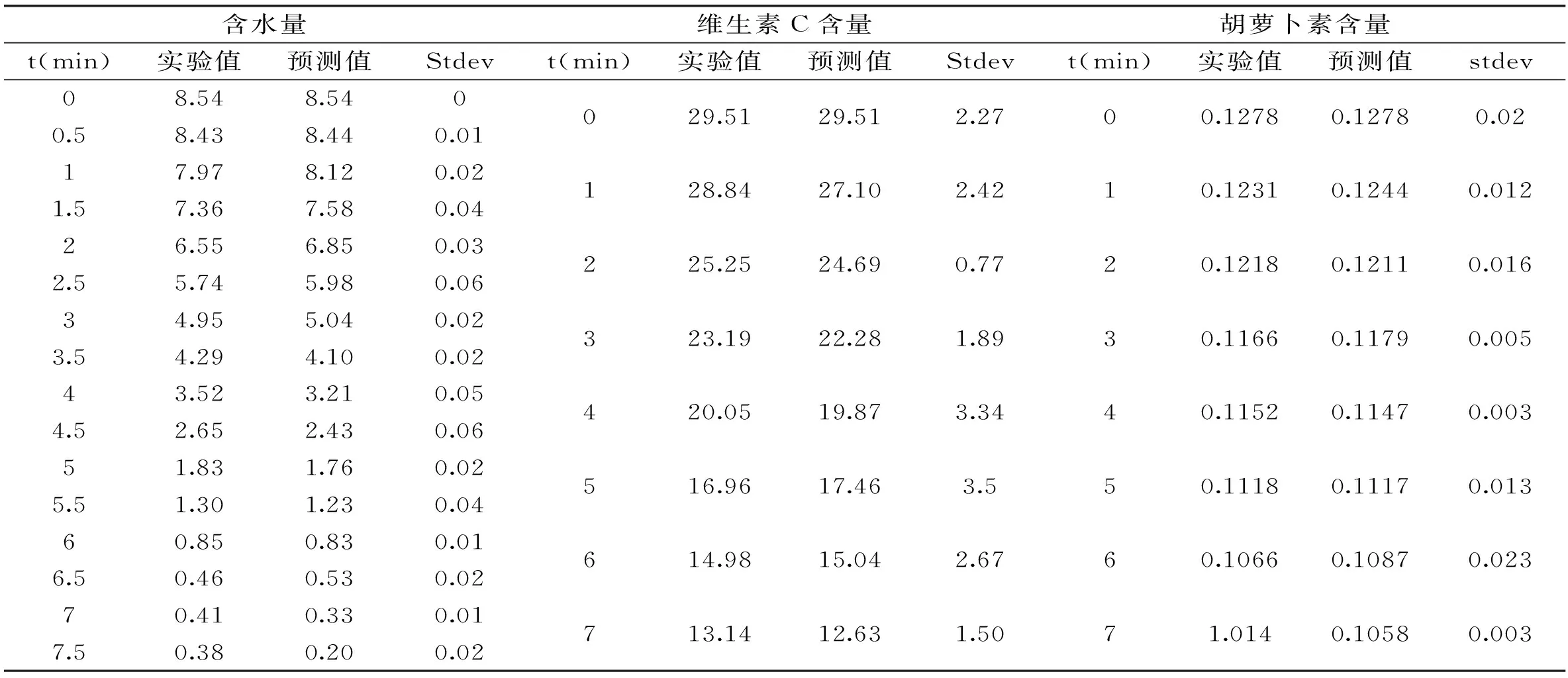
表8　600 W条件下实验值与预测值数据记录表

4　结论

番木瓜泡沫果浆在微波的作用下,其物料内部热量增加促使水分增发,同时也易引起物料中的维生素C和胡萝卜素等营养物质的被破坏。通过探究指数模型、单扩散模型和Page方程模型模拟水分含量变化规律,Page方程模型拟合度最高,得到水分含量变化动力学模型;使用零级反应模型和一级反应模型探究木瓜果浆微波泡沫过程中营养物质含量变化规律,得到模拟维生素C含量变化的零级反应方程和胡萝卜素含量变化的一级反应方程;

水分含量动力学方程:

维生素C含量动力学方程:

c=co-0.2411×p×t

胡萝卜素含量动力学方程:

C=C0×λ(-0.0027×p×t)

在500W以及600W条件下,对水分含量的Page方程模型、维生素C含量的零级反应模型以及胡萝卜素一级反应模型进行验证。从结果可以看出预测值与实验值接近,所得模型均能够极好的反映出干燥过程中对应物质的含量,说明所建立的模型具有极好的推广性。

本研究结果能够较准确的预测番木瓜微波泡沫干燥过程中水分含量、维生素C和胡萝卜素含量变化规律,有利于工业化生产过程中物料含水量和营养物质含量的检测,为番木瓜泡沫果浆微波泡沫干燥过程的优化和控制提供了理论依据。

[1]周鹏,沈文涛,言普,等. 我国番木瓜产业发展的关键问题及对策[J]. 热带生物学报,2010,01(3):257-260,264.

[2]袁志超,汪芳安. 番木瓜的开发应用及研究进展[J]. 武汉工业学院学报,2006,25(3):15-20.

[3]刘思,沈文涛,黎小瑛,等. 番木瓜的营养保健价值与产品开发[J]. 广东农业科学,2007(2):68-70.

[4]朱妞. 微波技术在食品工业中的应用及研究进展[J]. 中国调味品,2011,10(10):18-21.

[5]段振华,汪菊兰. 微波干燥技术在食品工业中的应用研究[J]. 食品研究与开发,2007(1):155-158.

[6]SankatCK,CastaigneF.Foaminganddryingbehaviorofripebananas[J].Lebensm-WissTechnology,2004,37:517-525.

[7]郑先哲,刘成海,周贺. 黑加仑果浆微波辅助泡沫干燥特性[J]. 农业工程学报,2009(8):288-293.

[8]张宝辉,郑先哲. 浆果微波辅助泡沫干燥品质和过程模拟研究[D]. 哈尔滨:东北农业大学,2014.

[9]张红卫,陈怀亮,刘忠阳. 基于MODIS数据的增强型土壤表层水分含量指数模型构建与应用[J]. 气象科技,2012,12(6):1039-1041.

[10]王强,任彦荣,蒲昌玖,等. 无核紫葡萄干燥特性及其总酚含量变化研究[J]. 食品科学,2015:1-8.

[11]林向阳,张丽晶,RogerRuan,等. 茶叶真空微波干燥特性及动力学模型[J].中国农学通报,2010,26(22):65-70.

[12]范新光,张长峰,肖璐,等. 减压处理鲜切西兰花的货架期预测模型构建[J]. 现代食品科技,2013,29(9):2120-2124.

[13]钟金峰,覃小丽,郑炯. 竹笋热烫处理过程中颜色变化的动力学模型[J]. 食品科学,2014,35(19):101-105.

[14]李秀伟,刘秉欣,陶岩,等. 浆果果浆微波泡沫干燥特性[J]. 农机化研究,2015(6):132-135.

[15]张建军,王海霞,马永昌,等. 辣椒热风干燥特性的研究[J]. 农业工程学报,2008,24(3):298-301.

[16]郭鹏飞. 番木瓜中番茄红素和β-胡萝卜素的制备及抗氧化性与稳定性研究[D]. 广州:暨南大学,2008.

[17]于海明. 山楂微波热风耦合干燥数学模型研究及干燥设备设计[D]. 长春:吉林大学,2015.

[18]周贺. 黑加仑果浆微波泡沫干燥工艺的研究[D]. 哈尔滨:东北农业大学,2009.

[19]郑先哲,张宝辉,梁玉朋,等. 微波辅助泡沫干燥过程中浆果营养成分降解模型[J]. 东北农业大学学报,2013(11):78-84.

[20]KrishnaMurthy.EffectofMicrowavePowerandSampleThicknessonMicrowaveDryingKineticsElephantFootYam(AmorphophallusPaeoniifolius)[J].AmericanJournalofFoodScienceandTechnology,2014,2(1):28-35.

[21]胡良平,高辉. 非线性回归分析与SAS智能化实现[M].北京:电子工业出版社,2013:34-36.

[22]郑宏. 温烫过程中芦笋(AsparagusofficinalisL)营养成分损失的预测以及调控研究[D]. 金华:浙江师范大学,2011.

[23]孙宇,郑先哲,李强,等. 微波辅助泡沫干燥蓝靛果果粉工艺的研究[J]. 东北农业大学学报,2012(5):17-23.

[24]Sari M,Karaaslan S. Microwave drying of pineapple and determination of suitable drying model[J]. Ziraat Fakültesi Dergisi-Süleyman Demirel üniversitesi,2014,9(1):42-50.

Model of the component degradation about foam-drying the papaya bubble by microwave

TANG Hui1,LI Meng-yu1,CHEN Wen-xue1,HU Yue-ying2,*

(1.College of Food Science and Technology,Hainan University,Haikou 570228,China;2.College of Materials and Chemical Engineering,Hainan University,Haikou 570228,China)

Based on the optimization of foam-drying the papaya bubble by microwave,the main materials content in the papaya was investigated. The rule of the moisture content and nutrition ingredient content was analyzed and studied under the different microwave power. And the best kinetic equation was verified by appropriate power. The results showed that the predictive value of Page equation model was well fitted for the experimental value when the moisture content was investigated and theR2was 0.9884.The zero order model of content of vitamin C was well fitted for the experimental value and theR2was 0.9702. And the first order reaction was most suitable for the content of carotene and theR2was 0.9185.There was no significant difference between predictive values and experimental values about the equation model. Models could be used to predict the dynamics characteristics of the main materials in papaya bubble in the process of foam-drying by microwave.

papaya pulp;foam-drying;microwave;model;model validation

2015-12-08

唐辉(1991-)，男，在读研究生，研究方向：热带农产品加工及应用微生物学，E-mail：877980232@qq.com。

胡月英(1971-)，女，硕士，助理研究员，研究方向：热带农产品加工及应用微生物学，E-mail：735844955@qq.com。

海南省产学研一体化专项(cxy20150032)。

TS255.1

A

1002-0306(2016)11-0089-08

10.13386/j.issn1002-0306.2016.11.010