一类带有参数的分数阶差分方程边值问题正解的存在性和不存在性
葛 琦, 侯成敏
( 延边大学理学院 数学系,吉林 延吉 133002 )
一类带有参数的分数阶差分方程边值问题正解的存在性和不存在性
葛琦, 侯成敏
( 延边大学理学院 数学系,吉林 延吉133002 )
研究一类带有参数的分数阶差分方程正解的存在性和不存在性。首先,分析该方程的格林函数的一些性质;然后,利用Banach空间锥上的不动点指数定理和Krasnosel'skii不动点定理,证明当参数属于不同范围时,该方程正解的存在性;最后,利用反证法,证明当参数属于不同范围时,该方程正解的不存在性。
Green函数; 不动点指数定理; 不动点定理; 不存在性
0 引言
近年来,随着分数阶差分方程理论研究的深入,关于分数阶差分方程解的存在性研究取得很大进展[1-17]。大多数文献在研究带有参数的分数阶差分方程边值问题时,只讨论正解的存在性[13,15-16],而关于其正解的不存在性的研究相对较少[17]。如2001年,Goodrich C S[13]研究成对的离散分数阶边值问题
正解的存在性,但未讨论正解的不存在性,其中,t∈[0,b]N0,1<νi≤2,λi>0,ai:R→(0,∞),Φi,Ψi:Rb+3→R是给定的泛函,fi:[0,+∞]×[0,+∞)⟹[0,+∞)是连续函数,i=1,2。
Kang Shugui等[16]于2014年研究阶数在(1,2]内的分数阶差分方程
正解的存在性,其中,1<ν≤2,t∈[0,b]N0,参数λ>0,f:[0,+∞)→[0,+∞)是连续函数,Φ,Ψ:Rb+3→R是给定的线性泛函,h:[ν-1,ν+b-1]Nν-1→[0,∞)。利用Krasnosel'kii不动点定理建立正参数λ属于不同区间时,方程存在一个正解和至少存在2个正解的充分条件,但对于正解的不存在性,文献没有讨论。
Han Zhenlai等[17]于2014年研究阶数在(1,2]内的分数阶差分方程
正解的存在性和不存在性,其中,1<ν≤2,t∈[0,b+1]N,λ是参数,f:[ν-1,ν+b]Nν-1×R→(0,+∞)是连续函数。也是利用Krasnosel'kii不动点定理,建立参数属于不同区间时,方程至少存在一个正解的充分条件,再利用反证法建立方程不存在正解的充分条件。
由于研究分数阶差分方程边值问题正解不存在性的文献相对较少,并且对于带有参数的分数阶差分方程,研究参数λ属于不同区间时,正解的存在性和不存在性具有一定的实际意义。笔者研究阶数在(2,3]内的分数阶差分方程
(1)
其中,2<ν≤3,0≤α,β<1,ν-β>2,参数λ>0,η∈[0,T-1]N0且满足下列条件:
(D1)f:[0,+∞)→[0,+∞)是连续函数;
(D2)g:[ν-1,T+ν-1]Nν-1→[0,+∞),且不恒为0。
首先将分别利用不动点指数定理和Krasnosel'skii不动点定理,建立当参数属于不同区间时,分数阶差分方程式(1)至少存在一个正解或2个正解的充分条件;再利用反证法建立方程式(1) 正解不存在的充分条件。
记Nα∶={a,a+1,a+2,…},[a,b]N0∶={a,a+1,a+2,…b}(b-a∈N1)。
1 预备知识
定义1[15]对于ν>0,函数f的ν阶分数和定义,有
对于N∈N,0≤N-1<ν≤N,函数f的ν阶分数差分定义有Δνf(t)=ΔNΔν-Nf(t)(t∈Na+N-ν)。
引理1[15]设N∈N,0≤N-1<ν≤N,那么Δ-νΔνy(t)+C1tν-1+C2tν-2+…+CNtν-N(Ci∈R,1≤i≤N)。

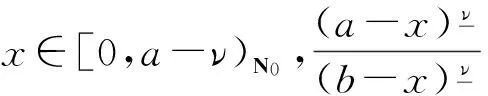
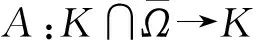
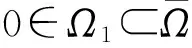
(A1)‖Sw‖≤‖w‖,w∈P∩∂Ω1;‖Sw‖≥‖w‖,w∈P∩∂Ω2;
(A2)‖Sw‖≥‖w‖,w∈P∩∂Ω1;‖Sw‖≤‖w‖,w∈P∩∂Ω2。
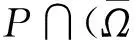
关于分数阶差分理论的相关基本概念和性质见文献[7-16]。
2 Green函数及其性质
定理1设2<ν≤3,0≤α,β<1,ν-β>2,η∈[0,T-1]N0,h(t+ν-1)∶[ν-1,T+ν-1]Nν-1→[0,+∞),则与方程式(1)有相同边值条件的方程
(2)
的唯一解是
(3)
这里记
(4)
(5)
证明由引理1有
由边值条件x(ν-3)=0得出C3=0。由于
则由边值条件[Δβx(t)]|t=ν-β-2=0,得出C2=0。再由边值条件x(T+ν)=αx(η+ν),得
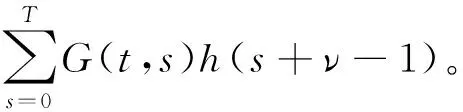
由此知式(3)成立。
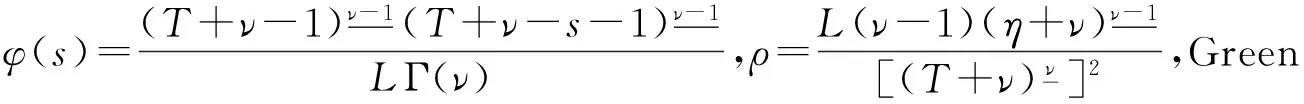
证明当0≤max{η+1,t-ν+1}≤s≤T时,记G(t,s)=g1(t,s); 当0≤η+1≤s 当0≤s 由G(t,s)的定义知,对于(t,s)∈[ν-1,T+ν-1]Nν-1×[0,T],有 当0≤η+1≤t-ν+1≤s≤T时,g1(t,s)>ρφ(s)显然成立。所以性质成立。 注1由定理2.2知,方程式(2)有解x(t)≥0,t∈[ν-3,T+ν]Nν-3。 由定理1知,求方程式(1)的解,等价于求方程 的解。先定义Banach空间B,即 并且范数为‖x‖=max|x(t)|,t∈[ν-3,T+ν-1]Nν-3。 定义B上的锥P0和P,即 定义算子A:B→B,即 (6) x是方程式(1)的解,当且仅当x是算子A的不动点。由于算子A是离散的有限集上的和算子,所以A是平凡完全连续算子。 引理6假设条件(D1)和(D2)成立,那么对于∀x∈P0有Ax∈P,特别,算子A是锥P到P上的映射。 证明对于∀x∈P0,由定理2.1和条件(D1),有(Ax)(t)≥0(t∈[ν-1,T+ν-1]Nν-1)。由定理2.2的知‖Ax‖。所以,对于∀x∈P有Ax∈P成立。 为了方便,记 (7) 定理3假设条件(D1)和(D2)成立,且f∞>0,f0<∞,N/f∞ 证明对于∀λ∈(N/f∞,M/f0),由f0 对于∀x∈P∩∂Ω1,当0<μ≤1,‖x‖=R时,有μAx≠x。 (8) 产生矛盾。因此,根据引理4有 (9) 注2如果f∞=∞,那么记N/f∞=0;如果f0=0,那么记M/f0=∞。定理3包含N/f∞=0,M/f0=∞的情形。 定理4假设条件(D1)和(D2)成立,且f0>0,f∞<∞,N/f0 由类似于定理3的证明可得,对于∀x∈P∩∂Ω3,当0<μ≤1,‖x‖=R3时,有μAx≠x。因此,算子满足引理4的条件,根据引理4有 (10) 另一方面,由N/f0<λ及f0的定义,存在常数R4(0 (11) 注3如果f0=∞,那么记N/f0=0;如果f∞=0,那么记M/f∞=∞。定理4包含N/f0=0、M/f∞=∞的情形。 注4由式(7)知,如果f∞N2>f0N1成立,那么当λ∈(1/(f∞N2)、1/(f0N1))时,定理3成立;如果f0N2>f∞N1成立,那么当λ∈(1/(f0N2),1/(f∞N1))时,定理4成立。 定理5假设条件(D1)和(D2)成立,且存在2个不同的正数r1、r2,使得 那么方程式(1)有一个解x∈P,且满足min{r1,r2}≤‖x‖≤max{r1,r2}。 证明设Ω5={x∈P0:‖x‖ 另外,设Ω6={x∈P0:‖x‖ 由引理5知方程式(1)有一个正解x∈P,且满足min{r1,r2}≤‖x‖≤max{r1,r2}。 记 (12) 根据条件(D1)和(H1),有0<λ1≤+∞和0≤λ2<+∞。 定理6假设条件(D1)、(D2)和(H1)成立,如果f0=+∞和f∞=+∞,那么对于∀λ∈(0,λ1),方程式(1)至少有2个正解。 因此有 (13) (14) 另外,由条件f0=+∞和f∞=+∞知,存在常数n1、n2(0 (15) (16) 由式(13)和式(15)、式(14)和式(16)及定理5知,对于∀λ∈(0,λ1),方程式(1)至少有2个正解。 推论1假设条件(D1)、(D2)和(H1)成立,如果f0=+∞或f∞=+∞,那么对于∀λ∈(0,λ1),方程式(1)至少有一个正解。 定理7假设条件(D1)、(D2)和(H1)成立,如果f0=0和f∞=0,那么对于∀λ∈(λ2,+∞),方程式(1)至少有2个正解。 (17) (18) 另外,由条件f0=0知,存在常数d3(0 (19) (20) 由式(17)和式(19)、式(18)和式(20)及定理5知,对于∀λ∈(λ2,+∞),方程式(1)至少有2个正解。 推论2假设条件(D1)、(D2)和(H1)成立,如果f0=0或f∞=0,那么对于∀λ∈(λ2,+∞),方程式(1)至少有一个正解。 首先建立方程式(1)不存在正解的充分条件。 定理8假设条件(D1)、(D2)和(H1)成立,如果f0<+∞和f∞<+∞,那么存在λ0>0,使得对于∀λ∈(0,λ0),方程式(1)不存在正解。 证明由于f0<+∞和f∞<+∞,那么存在正数l1,l2,r3和r4,使得r3 产生矛盾,所以方程式(1)不存在正解。 定理9假设条件(D1)、(D2)和(H1)成立,如果f0>0和f∞>0,那么存在λ0>0,使得对于∀λ∈(λ0,+∞),方程式(1)不存在正解。 证明由于f0>0和f∞>0,那么存在正数l3、l4、r5和r6,使得r5 产生矛盾,所以方程式(1)不存在正解。 利用Banach空间锥上的不动点指数定理和Krasnosel'skii不动点定理,研究一类带有参数的分数阶差分方程正解的存在性,利用反证法研究该方程正解的不存在性。分别建立当参数属于不同区间时,该方程存在正解和不存在正解的充分条件。 [1]Goodrich C S. Existence and uniqueness of solutions to a fractional difference equation with nonlocal conditions [J]. J.Comput. Math. Appl, 2011,61(2):191-202. [2]Goodrich C S. On a fractional boundary value problem with fractional boundary conditions [J]. Appl Math Lett, 2012,25(8):1101-1105. [3]Goodrich C S. Solutions to a discrete right-focal boundary value problem [J]. Int. J. Difference Equ, 2010,5(2):195-216. [5]Goodrich C S. On discrete sequential fractional boundary value problems [J]. J. Math. Anal. Appl, 2012,385(1):111-124. [6]Goodrich C S. Existence of a positive solution to a system of discrete fractional boundary value problems [J]. J. Applied Mathematics and Computation, 2011,217(9):4740-4753. [7]张瑜,孙明哲,何延生.一类分数阶差分方程解的吸引性[J].延边大学学报:自然科学版,2012,38(2):95-99. Zhang Yu, Sun Mingzhe, He Yansheng. Atrractivity of a class of fractional difference equations [J]. Journal of Yanbian University: Natural Science, 2012,38(2):95-99. [8]葛琦,侯成敏.一类分数阶差分方程边值问题多重正解的存在性[J].东北石油大学学报,2012,36(4):101-110. Ge Qi, Hou Chengmin. Existence of multiple positive solutions for a class of fractional difference equations boundary value problems [J]. Journal of Northeast Petroleum University, 2012,36(4):101-110. [9]葛琦,侯成敏.一类分数阶差分方程边值问题递增正解的存在性[J].吉林大学学报:理学版,2013,51(1):47-52. Ge Qi, Hou Chengmin. Existence of positive and nondecreasing solution for a class of fractional difference equations boundary value problems [J]. Journal of Jilin University: Science Edition, 2013,51(1):47-52. [10]慎闯,何延生.一类带有分数阶非局部边值条件的分数阶差分方程解的存在性[J].烟台大学学报:自然科学与工程版,2013,26(2):90-96. Shen Chuang, He Yansheng. Existence of solutions for a class of fractional difference equation with nonlocal fractional boundary conditions [J]. Journal of Yantai University: Natural Science and Engineering Edition, 2013,26(2):90-96. [11]慎闯,何延生,侯成敏.一类有序分数阶差分方程解的存在性[J]. 扬州大学学报:自然科学版,2013,16(1):12-16. Shen Chuang, He Yansheng, Hou Chengmin. Existence of solution for a class of sequential fractional difference equation [J]. Journal of Yangzhou University: Natural Science Edition, 2013,16(1):12-16. [12]Chen Fulai, Luo Xiannan, Zhou Yong. Existence results for nonlinear fractional difference equation [J]. J. Advances in Difference Equations, 2011,2011(1):1-12. [13]Goodrich C S. Existence of a positive solution to a system of discrete fractional boundary value problems [J]. Comput.Math. Appl. 2011,217(9):4740-4753. [14]Huang Zhongmin, Hou Chengmin. Solvability of nonlocal fractional boundary value problems [J].Discrete Dynamics in Nature and Society, 2013,2013(1):1-9. [15]艾尚明,卢源秀,高鹏,等.一类带有成对边界条件的奇异半正分数阶差分系统的正解[J].东北石油大学学报,2014,38(4):103-118. Ai Shangming, Lu Yuanxiu, Gao Peng, et al. Positive solutions for a class of singular semipositione fractional difference system with coupled boundary conditions [J]. Journal of Northeast Petroleum University, 2014,38(4):103-118. [16]Kang Shugui, Li Yan, Chen Huiqin. Positive solutions to boundary value problems of fractional difference equation with nonlocal conditions [J]. Advances in Difference Equations, 2014(1):1-12. [17]Han Zhenlai, Pan Yuanyuan, Yang Dianwu. The existence and nonexistence of positive solutions to a discrete fractional boundary value problem with a parameter [J]. Applied Mathematics Letters, 2014,36(1):1-6. [18]Dun Tiaoxia, Chen Pengyu. Existence of positive solutions for nonlinear third-order boundary value problems [J]. Journal of Mathematics, 2014(1):1-5. [19]Zhao Yige, Sun Shurong, Han Zhenlai. Positive solutions for boundary value problems of nonlinear fractional differential equations [J]. Applied Mathematics and Computation, 2011(217):6950-6958. 2015-12-07;编辑:关开澄 国家自然科学基金项目(11161049);吉林省教育厅“十二五”科技项目(吉教科合字[2015]第36号) 葛琦(1975-),女,硕士,副教授,主要从事微分方程理论及应用方面的研究。 10.3969/j.issn.2095-4107.2016.02.015 O175.6 A 2095-4107(2016)02-0112-09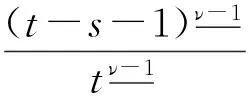
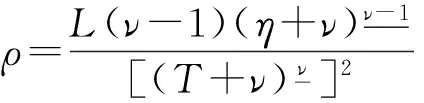
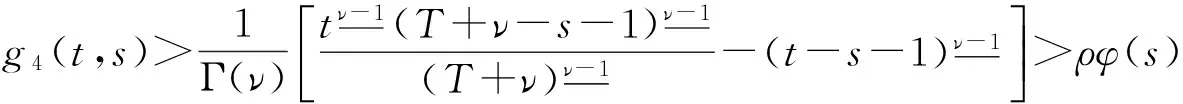
3 正解的存在性

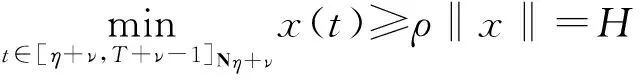
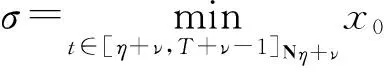
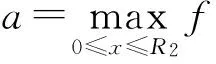
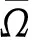
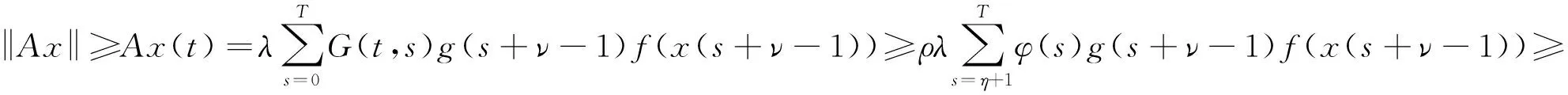

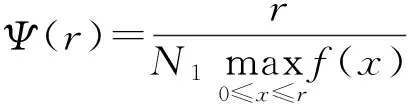
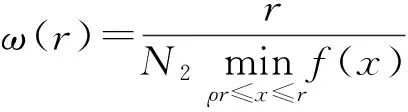
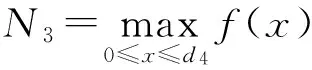
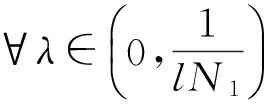
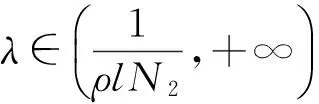
4 正解的不存在性

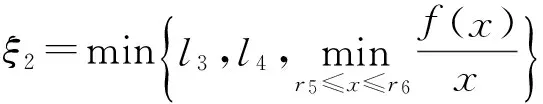
5 结束语

