低速非达西渗流动边界移动规律

王建俊， 鞠斌山， 罗二辉

( 1. 中国地质大学(北京) 能源学院，北京　100083；　2. 中国石油勘探开发研究院，北京　100083 )



低速非达西渗流动边界移动规律

王建俊1， 鞠斌山1， 罗二辉2

( 1. 中国地质大学(北京) 能源学院，北京100083；2. 中国石油勘探开发研究院，北京100083 )

低渗透油藏非达西渗流动边界的产生归因于启动压力梯度。在考虑动边界的基础上，建立包含表皮效应和井筒存储的单一、以Warren-Root模型为基础的双重和三重介质低速非达西渗流数学模型；并通过定义无量纲压力得到模型的Laplace解，利用Stehfest数值反演获得动边界的传播规律，对比动边界与无限大、封闭及定压等三类外边界条件下的压力及压力导数分布特征。结果表明：对于低速非达西渗流，启动压力梯度越大，动边界向外传播越慢；在双重介质和三重介质中，动边界移动出现短暂的停滞，曲线上表现为水平段或平缓段；动边界主要影响压力及压力导数曲线的中后期，而无限大、封闭及定压等三类外边界主要影响曲线的后期形态。

非达西渗流； 启动压力梯度； 动边界； 单一介质； 双重介质； 三重介质

0　引言

达西定律已广泛应用于多孔介质的渗流力学问题，当渗流速度过快或过慢时，达西定律描述的渗流速度与压力梯度之间的线性关系不再成立，偏离达西定律线性关系的渗流问题可以归结为非达西渗流。低速非达西渗流是指流速较慢而导致偏离达西定律的流动，如低渗透储层或深部弱透水层[1-2]。李凡华等[3]研究表明，当启动压力梯度值大于0时，压力的传播并非瞬时达到无穷远，可以采用数值离散化方法计算动边界随时间的变化；贾振岐等[4]通过实验证明，低渗透油藏的孔隙越小、喉道越窄、固液表面的分子作用力越强，启动压力越高；程时清等[5]对低速非达西动边界问题进行积分求解；闫栋栋等[6]通过气泡法岩心测试表明流度越低，启动压力梯度越高；计秉玉等[7]运用稳态逐次逼近方法，求解定流量和定流压条件下的非达西渗流模型；王晓冬等[8]采用数理方法，求解包含启动压力梯度和动边界的非线性不定常渗流数学模型；王军磊等[9]利用叠加原理，求解考虑启动压力梯度的七点井网稳态压力方程，表明启动压力梯度越大，有效动用程度越低。

当储层中存在溶洞、裂缝时，渗流通道不再是单一的孔隙介质，而是形成双重介质和三重介质。多重介质中低速非达西渗流问题更加复杂。姜瑞忠等[10]利用油藏工程方法，研究裂缝存在时形成的优势渗流通道。针对双重介质，罗二辉、程林松、Xu Jianchun等考虑启动压力梯度，得到非达西渗流的特征[11-13]。罗二辉等[14]利用解析方法，得到三重介质中压力分布，并分析敏感因素。由于低速非达西渗流具有高度非线性，难以获得解析解，目前还没有针对不同介质中动边界的移动规律的研究。在考虑动边界的基础上，基于启动压力梯度的非达西渗流，笔者建立包含表皮效应和井筒存储的单一、以Warren-Root模型为基础的双重[15]和三重介质[16]低速非达西渗流有效井径数学模型；利用Laplace变换和Stehfest数值反演获得压力分布的解析解表达式，分析不同介质类型中启动压力梯度对动边界传播规律的影响，并对比动边界与无限大、封闭及定压等三类外边界条件下的压力及压力导数的变化动态特征。

1　低速非达西渗流数学模型

1.1假定条件

(1)平面径向流动，储层厚度为h；(2)介质分别为单一、双重和三重孔隙介质且各向同性，外边界为无限大、封闭、定压、动边界等四类；(3)储层流体和岩石微可压缩；(4)动边界条件下符合低速非达西渗流，启动压力梯度为G；(5)考虑表皮效应和井筒存储，不考虑重力和毛管力。

1.2参数无量纲化

无量纲化可以使渗流方程变得简洁整齐，便于分析和求解。对渗流方程中参数进行无量纲化，包括压力、时间等，其中启动压力梯度的影响体现在孔隙介质压力与裂缝系统压力上。

其中:pi为原始地层压力；pd为单一介质中孔隙介质压力，pdD为对应的无量纲形式；pf为裂缝系统压力，pfD为对应的无量纲形式；pv为溶洞系统压力，pvD为对应的无量纲形式；pm为基质系统压力，pmD为对应的无量纲形式；pw为井底流动压力；kd为单一介质渗透率；kf为裂缝系统渗透率；km为基质系统渗透率；r为距井中心的距离，rD为对应的无量纲形式；rw为井筒半径；rf为压力扰动边界，rfD为对应的无量纲形式；μ为地下原油黏度；B为原油体积系数；t为生产时间，tD为对应的无量纲形式；q为油井产量；φ为单一介质储层孔隙度；φf为裂缝系统孔隙度；φm为基质系统孔隙度；φv为溶洞系统孔隙度；ct为单一介质地层压缩系数；cm为基质系统压缩系数；cf为裂缝系统压缩系数；cv为溶洞系统压缩系数；C为井筒存储系数，CD为对应的无量纲形式；S为井底附近表皮因子；GD为G的无量纲形式。

1.3渗流控制方程

根据连续性方程、运动方程和状态方程，建立低速非达西渗流微分方程的无量纲表达形式。

对于单一介质渗流微分方程(只存在孔隙介质系统)为

(1)

对于双重介质渗流微分方程(存在裂缝和基质系统)，其中裂缝系统的渗流方程为

(2)

基质系统的渗流方程为

(3)

式(2-3)中：λm为基质窜流系数；ωf为裂缝弹性储容比；ωm为基质弹性储容比。

对于三重介质渗流微分方程(存在裂缝、溶洞和基质系统)，其中裂缝系统的渗流方程为

(4)

溶洞系统的渗流方程为

(5)

基质系统的渗流方程为

(6)

式(4-6)中：λv为溶洞窜流系数；ωv为溶洞弹性储容比。

1.4定解条件

渗流控制方程必须在一定的定解条件下才能求得特定解，定解条件包括初始条件和边界条件。

(1)初始条件为

(7)

(2)边界条件分为内边界条件和外边界条件。其中，内边界定产，外边界分为4种，无量纲表达。

内边界定产条件为

(8)

对于外边界条件，无限大外边界条件为

(9)

封闭外边界条件为

(10)

定压外边界条件为

(11)

动边界条件为

(12)

(13)

2　有限井径Laplace解

对式(1-13)作Laplace变换(tD/CD→u，u为Laplace变换量)。

渗流控制方程式(1-6)统一转化为

(14)

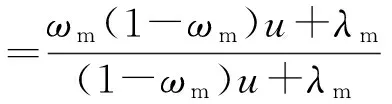
对定解条件进行转化，内边界条件为

(15)

外边界条件分别为

(16)

(17)

(18)

(19)

(20)

式(14-20)中：

根据式(15-20)，求解渗流控制方程式(14)，得到相应的Laplace空间压力分布解。

无限大外边界Laplace解为

(21)

封闭外边界Laplace解为

(22)

定压外边界Laplace解为

(23)

动边界Laplace解为

(24)

利用贝塞尔函数相应的Wronskians关系式，将式(24)代入式(20)，得到动边界传播方程为

(25)

式(21-25)中：I0(x)、I1(x)分别为0阶、1阶第一类变型贝塞尔函数；K0(x)、K1(x)分别为0阶、1阶第二类变型贝塞尔函数。

对前三类边界条件，直接应用Stehfest数值反演式(21-23)，求得实空间解。动边界条件下的计算过程：首先利用Newton迭代法，在Laplace域中计算动边界传播方程式(25)；再利用Stehfest数值反演方法计算动边界条件下的解析式(24)，获得实空间下任意时刻低渗透储层无量纲压力和压力导数曲线。

3　压力及压力导数曲线

低渗储层非达西渗流动边界条件对压力分布的变化产生影响，由式(21-24)得到无限大、封闭、定压及动边界条件下压力及压力导数的分布特征，并分析动边界条件下特征与其他三种边界条件下的不同。

不同介质系统中，四种外边界条件下压力及压力导数的分布特征有明显的差异性(见图1-3)。由图1-3可以看出，三种介质中，无限大、封闭及定压等三类外边界效应主要影响晚期流动，其中无限大外边界压力导数晚期为一斜率等于0的水平线；封闭外边界出现上翘；定压外边界出现下掉。动边界对中期流动也具有一定影响，在井筒存储和表皮效应流动段后的某一个时间点，压力导数曲线出现缓慢抬升，且最终上翘程度比封闭边界的要小。低渗透储层中启动压力梯度的存在使渗流过程中阻力增加，即动边界的影响介于无限大和封闭边界的影响之间，若简单地将低渗透油藏中的动边界简化成无限大或封闭边界，则导致压力及压力导数特征分析中产生误差。

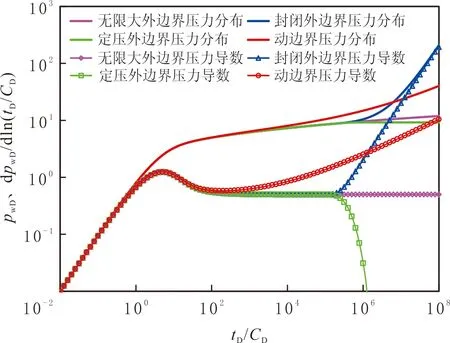
图1　四类外边界对单一介质压力及压力导数曲线的影响Fig.1 Distribution of pressure and pressure derivate in single-porosity media with four different types of boundaries

图2　四类外边界对双重介质压力及压力导数曲线的影响Fig.2 Distribution of pressure and pressure derivate in dual-porosity media with four different types of boundaries

与单一介质相比，双重介质中，压力导数曲线存在一个“凹子”，下凹表明基质与裂缝之间流体交换的典型特征，且在下凹后，动边界作用下的压力导数曲线逐渐上翘(见图2)，与其他三种外边界条件下的特征有显著不同。三重介质中，压力导数曲线上有两个“凹子”，符合三重介质的典型特征，即第一个“凹子”表示三重介质溶洞对裂缝的补给；第二个“凹子”表示基质系统对裂缝系统的供液，与其他三种外边界条件相比，动边界作用下的压力导数曲线第二个“凹子”的下凹程度较小；在第二个下凹后，动边界作用下的压力导数曲线逐渐上翘，但上翘幅度低于封闭外边界压力导数曲线的(见图3)。

4　动边界移动曲线

根据动边界传播方程式(25)，得到单一介质、双重介质及三重介质中不同启动压力梯度下的动边界传播规律(见图4-6)。由图4-6可以看出，启动压力梯度越大，压力扰动边界越小，即动边界移动越慢；同时说明动边界的存在使得地层能量消耗增加，启动压力梯度越大，能量消耗越大。

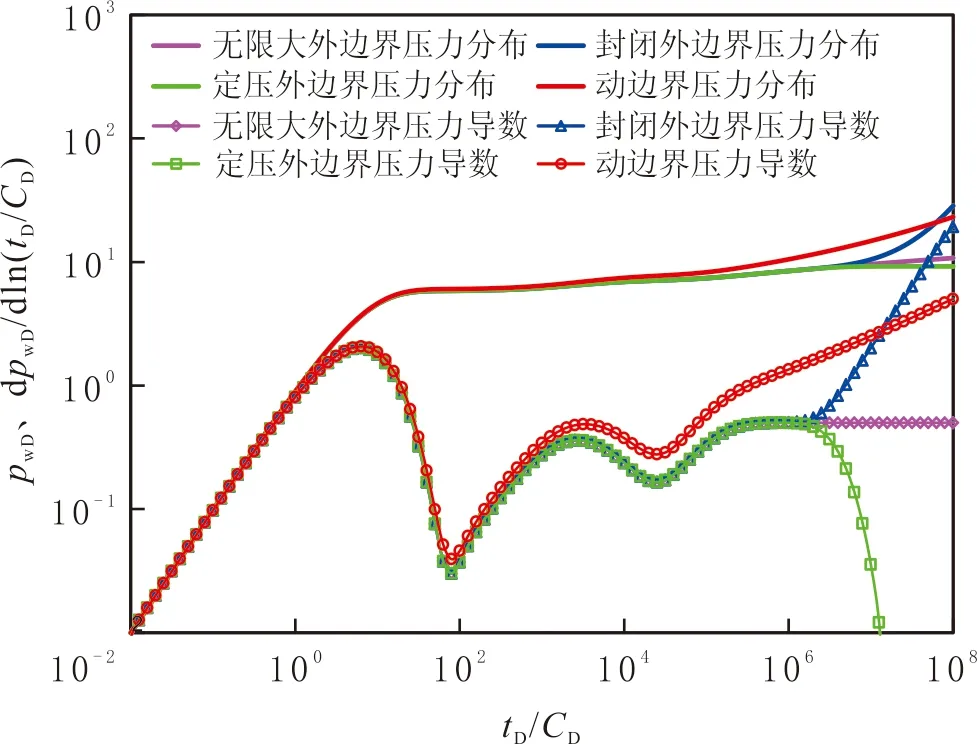
图3　四类外边界对三重介质压力及压力导数曲线的影响Fig.3 Distribution of pressure and pressure derivate in triple-porosity media with four different types of boundaries

图4　不同启动压力梯度下单一介质动边界移动规律Fig.4 The movement of dynamic boundary in single-porosity media with different threshold pressure gradient

与单一介质相比，在中期阶段，双重介质中压力扰动边界随时间的变化曲线出现斜率为0的水平段(见图5)，在这一水平段时间里，动边界停止移动，即出现停滞现象。原因在于基质向裂缝进行供液，当供液结束后，动边界继续移动。对比双重介质压力与压力导数分布特征曲线(见图2)，在中期阶段tD/CD≈102时，压力导数曲线出现下凹，即基质向裂缝供液，证实动边界移动规律的正确性。

三重介质中，在中期阶段，动边界移动曲线上出现两个相对平缓段(见图6)。第一个平缓段斜率为0，表明此时间段动边界停止移动；而第二个平缓段比第一个平缓段陡一些，表明此时间段动边界的移动相当缓慢。原因是溶洞系统向裂缝供液导致第一个平缓段的产生，第二个平缓段的产生源自基质向裂缝的拟稳态窜流，而且溶洞中的流体比基质中的流体更容易流入裂缝，即供液能力不同，导致两个平缓段的斜率不同。对比三重介质压力与压力导数分布特征曲线(见图3)，压力导数曲线出现两个下凹，验证动边界移动规律的可靠性。

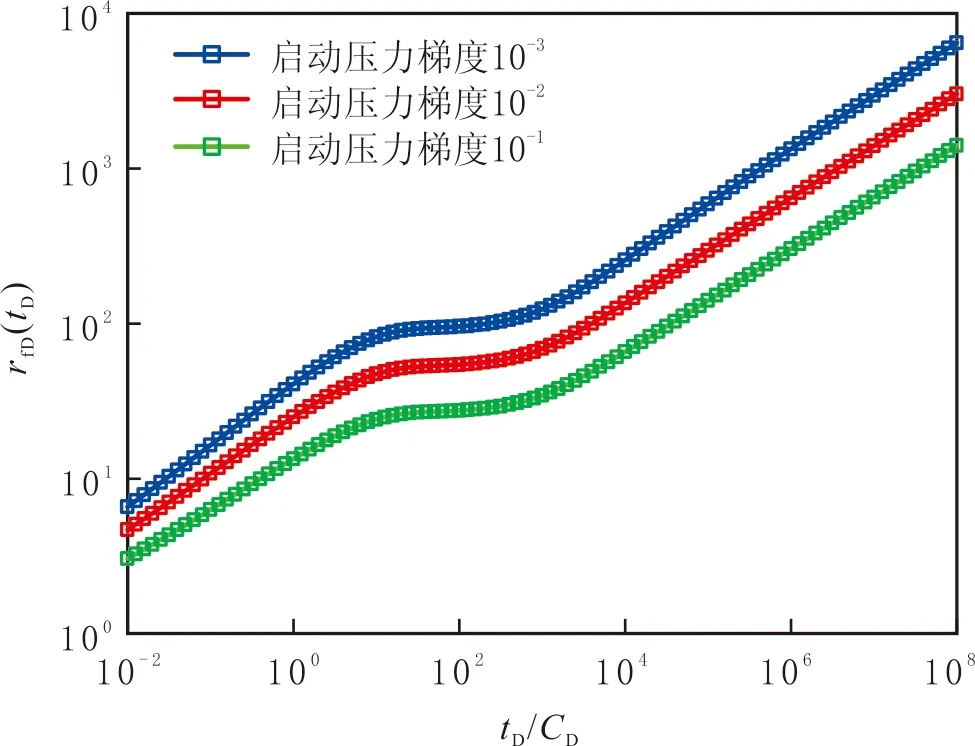
图5　不同启动压力梯度下双重介质动边界移动规律Fig.5 The movement of dynamic boundary in dual-porosity media with different threshold pressure gradient

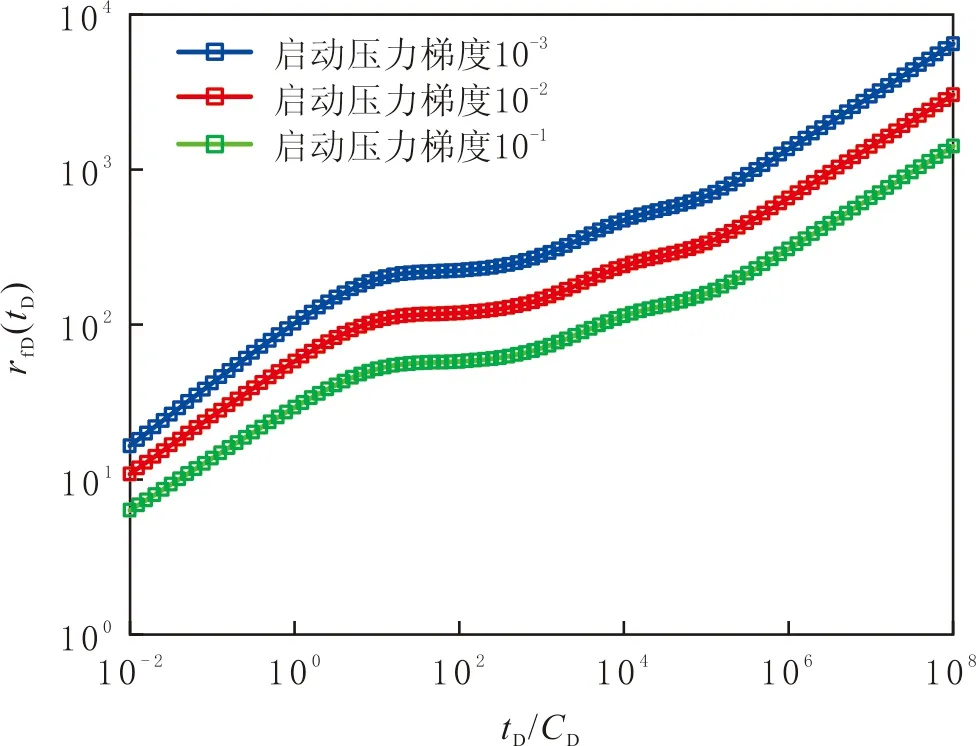
图6　不同启动压力梯度下三重介质动边界移动规律Fig.6 The movement of dynamic boundary in triple-porosity media with different threshold pressure gradient

5　结论

(1)考虑动边界效应，定义包含启动压力梯度的无量纲压力，建立考虑表皮效应和井筒存储的三种不同介质类型的非达西渗流数学模型。采用Laplace变换和Newton迭代法求解动边界方程和压力控制方程。

(2)与无限大、封闭及定压三类外边界相比，低渗储层中非达西渗流动边界条件下的压力及压力导数分布特征具有明显差异。动边界作用下，无量纲压力及压力导数曲线在中后期上翘，说明在低渗透储层开发过程中需要相对较大的能量。

(3)计算得出单一、双重和三重介质中的动边界移动规律，随启动压力梯度的增加，动边界向外移动传播速度减缓。在双重介质和三重介质动边界移动曲线上出现水平段或者平缓段，表明了动边界的移动具有停滞性，而不存在启动压力梯度的中高渗流储层中不会出现此现象。

[1]冯文光,葛家理.单一介质、双重介质中非定常非达西低速渗流问题[J].石油勘探与开发,1985,12(1):56-62.

Feng Wenguang, Ge Jiali. The unsteady non-Darcy flow in single-porosity and dual-porosity porous media [J].Petroleum Exploration and Development, 1985,12(1):56-62.

[2]谢海澜,武强,赵增敏,等.考虑非达西流的弱透水层固结计算[J].岩土力学,2007,28(5):1061-1065.

Xie Hailan, Wu Qiang, Zhao Zengmin, et al. Consolidation computation of aquitard considering non-Darcy flow [J]. Rock and Soil Mechnics, 2007,28(5):1061-1065.

[3]李凡华,刘慈群.含启动压力梯度的不定常渗流的压力动态分析[J].油气井测试,1997,6(1):1-4.

Li Fanhua, Liu Ciqun. Pressure tansient analysis for unsteady porous flow with start-up pressuere derivative [J]. Well Testing, 1997,6(1):1-4.

[4]贾振岐,王延峰,付俊林,等.低渗低速下非达西渗流特征及影响因素[J].大庆石油学院学报,2001,25(3):73-76.

Jia Zhenqi, Wang Yanfeng, Fu Junlin, et al. Characteristics of non-Darcy percolation and under the condition of low-permeability and low-velocity [J]. Journal of Daqing Petrpleum Institute, 2001,25(3):73-76.

[5]程时清,张盛宗,黄延章,等.低速非达西渗流动边界问题的积分解[J].力学与实践,2002,24(3):15-17.

Cheng Shiqing, Zhang Shengzong, Huang Yanzhang, et al. An integral solution of free-boundary problem of non-Darcy flow behavior [J]. Mechanics and Engineering, 2002,24(3):15-17.

[6]闫栋栋,杨满平,王刚,等.低流度油藏启动压力梯度分析[J].大庆石油学院学报,2010,34(1):39-42.

Yan Dongdong, Yang Manping, Wang Gang, et al. Threshold pressuere gradient analysis for low mobility reservoir [J]. Journal of Daqing Petrpleum Institute, 2010,34(1):39-42.

[7]计秉玉,何应付.基于低速非达西渗流的单井压力分布特征[J].石油学报,2011,32(3):466-469.

Ji Bingyu, He Yingfu. Formation pressure distribution of a single well based on low velocity non-Darcy flow [J]. Acta Petrolei Sinica, 2011,32(3):466-469.

[8]王晓冬,侯晓春,郝明强,等.低渗透介质有启动压力梯度的不稳定压力分析[J].石油学报,2011,32(5):847-851.

Wang Xiaodong, Hong Xiaochun, Hao Mingqiang, et al. Pressure transient analysis in low-permeability media with threshold gradients [J]. Acta Petrolei Sinica, 2011,32(5):847-851.

[9]王军磊,周明旺,罗二辉,等.低渗透油藏七点井网的有效动用程度[J].东北石油大学学报,2013,37(2):102-106.

Wang Junlei, Zhou Mingwang, Luo Erhui, et al. Effective development degree for seven-spot well patterns in low permeability reservoirs [J]. Journal of Northeast Petroleum University, 2013,37(2):102-106.

[10]姜瑞忠,于成超,孔垂显,等.低渗透油藏优势渗流通道模型的建立及应用[J].特种油气藏,2014,21(5):85-88.

Jiang Ruizhong, Yu Chengchao, Kong Chuixian, et al. Establishment and application of dominant seepage path model of low-permeability oil reservoirs [J]. Special Oil & Gas Reservoirs, 2014,21(5):85-88.

[11]罗二辉,王晓冬.双重低渗介质含启动压力梯度不定常渗流研究[J].中国海上油气,2011,23(5):318-321.

Luo Erhui, Wang Xiaodong. A study on transient flow under threshold pressure gradient in dual-pore media with low permeability[J]. China Offshore Oil and Gas, 2011,23(5):318-321.

[12]程林松,任胜利,廉培庆.动边界双重介质油藏低速非达西渗流试井模型[J].计算力学学报,2011,28(6):879-883.

Cheng Linsong, Ren Shengli, Lian Peiqing. Well test analysis on low velocity and non-Darcy flow in dual-porosity reservoir with dynamic boundary [J]. Chinese Journal of Computational Mechanics, 2011,28(6):879-883.

[13]Xu Jianchun, Jiang Ruizhong, Xie Lisha, et al. Transient pressure behavior for dual porosity low permeability reservoir based on modified Darcy's equation [C]. SPE 153480, 2012.

[14]罗二辉,胡永乐.三重介质低渗油藏非达西非稳态渗流研究[J].中国矿业大学学报,2013,42(1):100-104.

Luo Erhui, Hu Yongle. A study of non-Darcy transient flow in triple porosity media with low permeability reservoir [J]. Journal of China University of Mining Technology, 2013,42(1):100-104.

[15]Warren J E, Root P J. The behavior of naturally fractured reservoirs [J]. SPE Journal, 1963,3(3):245-255.

[16]Abdassah D, Ershaghi I. Triple-porosity systems for representing naturally fractured reservoirs [J]. SPE Formation Evaluation, 1986,1(2):113-127.

2015-11-13；编辑：刘丽丽

国家科技重大专项(2011ZX05016-006)；中央高校基本科研业务费专项资金项目(35832015034)

王建俊(1986-)，女，博士研究生，主要从事油气藏工程与渗流机理方面的研究。

10.3969/j.issn.2095-4107.2016.02.009

TE312

A

2095-4107(2016)02-0071-07