一类黎卡提方程逼近解的求法

吴　洁，胡　农（天津中德职业技术学院 基础课部，天津 300350）

一类黎卡提方程逼近解的求法

吴洁，胡农
（天津中德职业技术学院 基础课部，天津 300350）

摘要：首先，针对一类特殊的黎卡提方程，提出一种求其逼近解的方法，得到了该方程逼近解的表达式.其次，基于该方法，并利用换元法，得到了另一类黎卡提方程的逼近解.最后，讨论了逼近解的收敛性问题.

关键词：黎卡提方程；逼近解；待定函数；换元法；收敛性

对于一阶微分方程y′=f（x，y），设右端函数f（x，y）为一个关于y的二次多项式，该方程可表示为

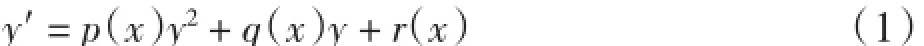
其中：函数p（x）、q（x）和r（x）在区间I上连续，而且p（x）≠0.方程（1）即为黎卡提方程.

黎卡提方程是形式最简单的非线性方程.Liouville已证明它不能用初等积分法求解［1］.许多学者从不同角度对黎卡提方程进行了研究.文献［2］在已知黎卡提方程特解的条件下，利用变量变换得到了其通解.文献［3］给出了周期系数黎卡提方程存在周期解的一个充分条件.文献［4］通过定义黎卡提方程的广义反射函数寻找其周期解，并分析了周期解的稳定性.文献［5］探讨了二阶变系数线性微分方程和黎卡提方程之间的内在联系.文献［6］通过齐次平衡原理和G′/G展开法求解黎卡提方程，得到了满足一定条件的黎卡提方程的G′/G解.本研究针对一类特殊的黎卡提方程，得到了其逼近解的表达式，并讨论了逼近解的收敛性问题.

1　逼近解的求解方法

考虑如下形式的黎卡提方程：

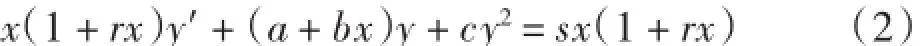
函数序列｛f（nx）｝满足

r2n+1=0.具体推导过程如下：

设y=（fx）+g（x）/y1为方程（2）的解，将其代入方程（2）并化简，则有

将上式变形为关于y1的方程，可得

为使方程（2）和方程（4）的形式相同，设g（x）=x（1+ rx），将g（x）代入方程（4），则方程（4）变为

设（fx）=mx+n（m、n待定），将（fx）代入方程（5），则方程（5）变为

为使方程（2）和方程（6）的形式相同，令an+cn2=0，即n=-a/c，代入方程（6），则方程（6）变为

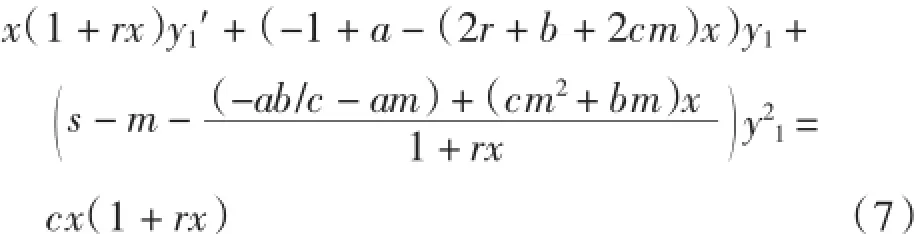
当m=-ar/c时，将其代入方程（7），则方程（7）变为

设a1=a-1，b1=-b+2ar-2r，c1=s+（ar-a2r+ab）/c，则方程（8）变为

可以看出方程（2）和方程（9）形式相同，而此时

因此有y=（fx）+g（x）/y1=-ar/cx-a/c+x（1+rx）/y1，故cy=-a（1+rx）+cx（1+rx）/y1.类似前面方法，可设y1=f（1x）+g（1x）/y2，重复上述过程，可得

其中：常数列｛an｝、｛bn｝满足：

令c0=c，由数学归纳法不难得到

由此可得方程（2）的逼近解为式（3）.

当m=-b/c时，同理可得方程（2）与cy=f（0x）类似的逼近解.

下面考虑黎卡提方程

将x、y、y′代入方程（10）并化简，可得

方程（11）即是方程（2）在r=-1时的情形，由方程（2）的逼近解式（3）可得方程（11）的逼近解，进而得到方程（10）的逼近解为

函数序列｛g（nx）｝满足

其中：αn=-a+n；γ2n=sc+（a-n）（b-n），γ2n+1=sc+ （n+1）（b-a+n+1）.

2　逼近解的收敛性

对于序列

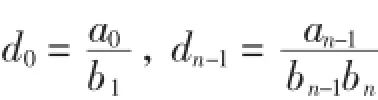
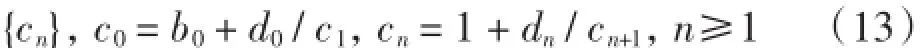
的连分式c0.对于序列（13）的连分式c0，有如下结论.

下面讨论方程（10）的逼近解式（12）的收敛性.

当n=2k-1时，有

3　结语

本研究针对一类特殊的黎卡提方程，得到了其逼近解的表达式，并讨论了逼近解的收敛性问题.在一些特殊的情况下，由本研究结果可得到方程（2）的特解，如当a=1，b=-1，c=1，s=1，r=0时，方程（2）为x（1+x）y′+（1-x）y+y2=x（1+x），这时由式（3）可得y=-x-1即为该方程的特解，而在已知方程特解的情况下，可通过换元法将黎卡提方程变为伯努利方程，进而利用初等积分法得到方程的通解.

参考文献：

［1］王高雄，周之铭.常微分方程［M］.3版.北京：高等教育出版社，2006. WANG G X，ZHOU Z M.Ordinary Differential Equation［M］.3rd ed. Beijing：Higher Education Press，2006（in Chinese）.

［2］贾庆菊，冯文俊，武跃祥.某些黎卡蒂（Riccati）方程的解［J］.中央民族大学学报：自然科学版，2013，22（1）：48-51. JIA Q J，FENG W J，WU Y X.The solution of some Riccati equations ［J］.Journal of MUC：Natural Sciences Edition，2013，22（1）：48-51 （in Chinese）.

［3］陈敏.关于Riccati方程的一个结论［J］.福州大学学报：自然科学版，2013，41（6）：954-957. CHEN M.A result for Riccati equation［J］.Journal of Fuzhou University：Natural Science Edition，2013，41（6）：954-957（in Chinese）.

［4］孙长军.Riccati方程的广义反射函数与周期解［J］.辽宁工程技术大学学报：自然科学版，2011，30（4）：576-578. SUN C J.Generalized reflection function and periodic solution of Riccati equation［J］.Journal of Liaoning Technical University：Natural Science，2011，30（4）：576-578（in Chinese）.

［5］胡劲松.二阶变系数线性微分方程与Riccati方程的关系［J］.大学数学，2009，25（1）：163-167. HU J S.The relation between the various coefficient linear differential equation of order 2 and Riccati equation［J］.College Mathematics，2009，25（1）：163-167（in Chinese）.

［6］魏帅帅，李凯辉，刘汉泽.G′/G展开法在Riccati方程中的应用［J］.河南科技大学学报：自然科学版，2015，36（5）：92-96. WEI S S，LI K H，LIU H Z.Application of G′/G expansion method in Riccati equation［J］.Journal of Henan University of Science and Technology：Natural Science，2015，36（5）：92-96（in Chinese）.

［7］哈凡斯基A H.连分式及其推广在近似分析问题上的应用［M］.叶乃膺，译.北京：科学出版社，1962. ФОВАНСКИЙ A H.The Applications of Continued Fraction and Its Extension on Approximate Analysis［M］.Translated by YE N Y.Beijing：Science Press，1962（in Chinese）.

（责任编校马新光）

第一作者：吴洁（1965—），女，副教授，主要从事计算数学方面的研究.

文章编号：1671-1114（2016）01-0040-08

中图分类号：O175.1

文献标志码：A

收稿日期：2015-03-14

A method for finding approximate solutions for a type of Riccati equations

WU Jie，HU Nong
（Basic Courses Department，Tianjin Sino-German Vocational Technical College，Tianjin 300350，China）

Abstract：Firstly，A method for finding approximate solutions for a type of Riccati equations is presented，and the expression of the approximate solution is obtained.Secondly，by using the method of substitution，the approximate solution of another type of Riccati equations is given based on the method.Finally，the convergence of approximate solutions is discussed.

Keywords：Riccati equation；approximate solution；undetermined function；method of substitution；convergence