恰含1个n圈和2个s圈的本原有向图的scrambling指数

宋卓蓉，高玉斌（中北大学 数学系，太原 030051）

恰含1个n圈和2个s圈的本原有向图的scrambling指数

宋卓蓉，高玉斌
（中北大学 数学系，太原 030051）

摘要：在图Ds，n的基础上，增加1个s长圈.研究含有1个n长圈和2个s长圈（2个s长圈有公共顶点）的本原有向图.通过分析图中每个点经过t长途径所到达的点的集合及点的个数，得出此类本原有向图的scrambling指数.

关键词：本原有向图；scrambling指数；圈

1　引言与预备知识

2009年，Akelbek等［1］将本原有向图本原指数的概念进行了推广，提出了scrambling指数的概念.几年来，该研究已经取得了许多成果.文献［2-3］得到了n阶本原有向图 scrambling指数的上界，并对scrambling指数达到上界的图进行了刻画.文献［4］提出了一种求本原有向图scrambling指数的新方法，并解决了含有d个环的本原有向图的scrambling指数的问题.文献［5］对本原对称有向图的scrambling指数进行了详细研究.文献［6］以非记忆通讯系统为背景，对scrambling指数进行了推广，引入了广义scrambling指数的概念.文献［7］研究了本原有向图指数集的问题.文献［8-10］得到了一些特殊的本原有向图的scrambling指数或广义scrambling指数.本研究考虑含有1个n长圈和2个s长圈的本原有向图，得到了此类本原有向图的scrambling指数.

设D=（V，E）是一个n阶有向图，其顶点集V= V（D），弧集E=E（D）（允许有环但无重弧）.

定义1［1］称有向图D是本原的，当且仅当存在正整数k，使得D中的任意一点x到另外一点y（y可能等于x）都存在k长途径.称满足上述条件的最小正整数k为有向图D的本原指数，记为exp（D）.

设D是一个n阶本原有向图，k∈Z+，对于任意顶点x、y∈V（D），用N+（Dk：x）表示顶点x经过k长途径所到达的点的集合，用N+（Dk：x，y）=N+（Dk：x）∩N+（Dk：y）表示顶点x、y经过k长途径所到达的公共点的集合，用|A|表示集合A中元素的个数.

定义2［1］设D是n阶本原有向图，如果存在正整数k，对D中任意顶点u和v，都存在顶点w∈V（D），使得从u和v到w都有k长途径，称满足上述条件的最小正整数k为本原有向图D的scrambling指数，记为k（D）.

称ku，v（D）=min｛k：|N+（Dk：u，v）|≥1｝为顶点u、v的局部scrambling指数［1］.称ku（D）=min｛k：u与Dk的任意顶点均有公共外邻域｝为顶点u的局部scrambling指数［1］.

显然，

引理［1］若D为含有1个n圈和1个s圈的本原有向图，gcd（n，s）=1，则k（D）≤K（n，s）.当且仅当D=Ds，n时（Ds，n如图1所示），有K（n，s）=k（n，s）+ n-s且

图1　本原有向图Ds，nFig.1　Primitive digraph Ds，n

2　主要结论

设n≥7，gcd（n，s）=1，D是恰含1个n圈和2 个s圈的n阶本原有向图.D（n；s，s）表示全部仅含1 个n圈和2个s圈（2个s长圈有公共顶点）的n阶本原有向图D组成的集合.下面将给出D（n；s，s）中所有本原有向图的scrambling指数.在证明过程中，顶点的指标按mod n看待.如，vn+1=v1，vn+2=v2，v0= vn，v-1=vn-1，v-2=vn-2等.

定理设D是如图2所示的n阶本原有向图，D∈D（n；s，s），gcd（n，s）=1，n-s+1≤t≤n-1，则

证明情形1.s为偶数.

首先证明k（D）≤t-s+（n-1）s/2，即证明对任意u、v∈V（D），均有k（D：u，v）≤t-s+（n-1）s/2. 在D中，顶点vt-s，vt-s+1，…，vt-1形成1个s长圈，记为C1.顶点vn-s，vn-s+1，…，vn-1形成1个s长圈，记为C2.任取vi、vj∈V（D），总存在x、y∈V（C1）∪V（C2），使得vit→-sx，vjt→-sy.

图2　本原有向图DFig.2　Primitive digraph D

设

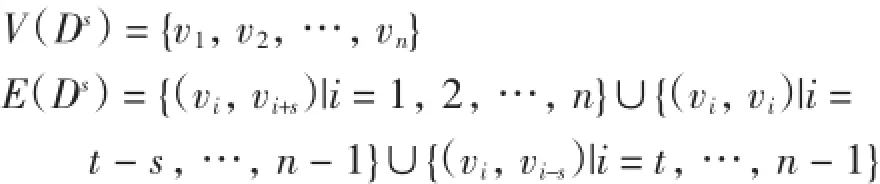
顶点vt-s，vt-s+1，…，vt-1和顶点 vn-s，vn-s+1，…，vn-1在Ds中均为环点.

设l=t-s+（n-1）s/2.因为

则对任意u、v∈V（D），均有 N（+Dl：u，v） ≥（n+1）/ 2+（n+1）/2-n=1，故k（D：u，v）≤t-s+（n-1）· s/2.由u、v的任意性可知k（D）≤t-s+（n-1）s/2.

下面证明k（D）≥t-s+（n-1）s/2.因为

故有N（+Dl-1：vs/2，vn）=，所以k（D）≥l=t-s+（n-1）s/2.

综上可得k（D）=t-s+（n-1）s/2.

情形2.s为奇数.

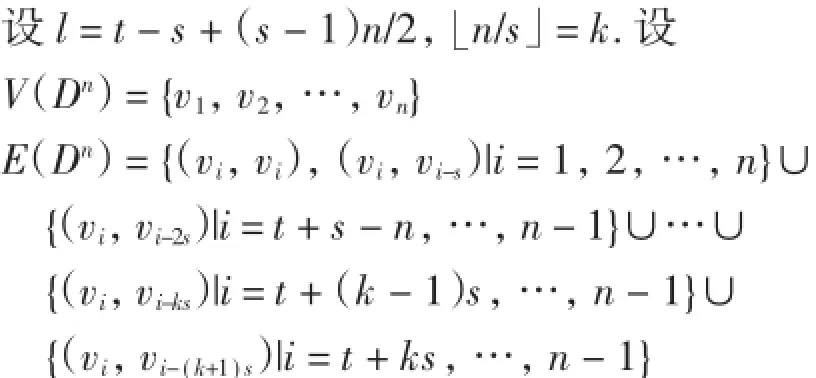
顶点v1，v2，…，vn形成1个n圈.记这个n圈为M.

情形2.1n为奇数.

情形2.1.1t-s≥n-t.

首先证明k（D）≤t-s+（s-1）n/2.在图D中，任取u、v∈V（D），总存在C1中的点vi、v（ji，j=t-s，…，t-1），使得ut→-svi，vt→-svj.所以只需证明对任意i，j=t-s，…，t-1，均有k（D：vi，v）j≤（s-1）n/2.

在Dn中，令M1=Dn［｛vt-s，…，vt-1｝］，M1为Dn的一个导出子图.M1中顶点vt-s，…，vt-1均为环点并构成1个s圈，则对任意vi、vj∈V（M1），均有中，任取u、v∈V（D），均有k（D：u，v）≤t-s+（s-1）n/2.

下面证明k（D）≥t-s+（s-1）n/2.

当k为奇数时，有

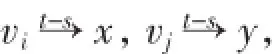
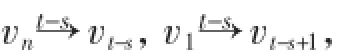
所以对任意u、v∈V（D），均有k（D：u，v）≤ts+（s-1）n/2.

下面证明k（D）≥t-s+（s-1）n/2.因为

综上可得k（D）=t-s+（s-1）n/2.

情形2.2 n为偶数.

情形2.2.1 t-s≥n-t.

利用情形2.1.1的方法，可证得在图D中任取u、v∈V（D），均有k（D：u，v）≤t-s+（s-1）n/2.

下面证明k（D）≥t-s+（s-1）n/2.

当k为奇数时，

当k=2时，有

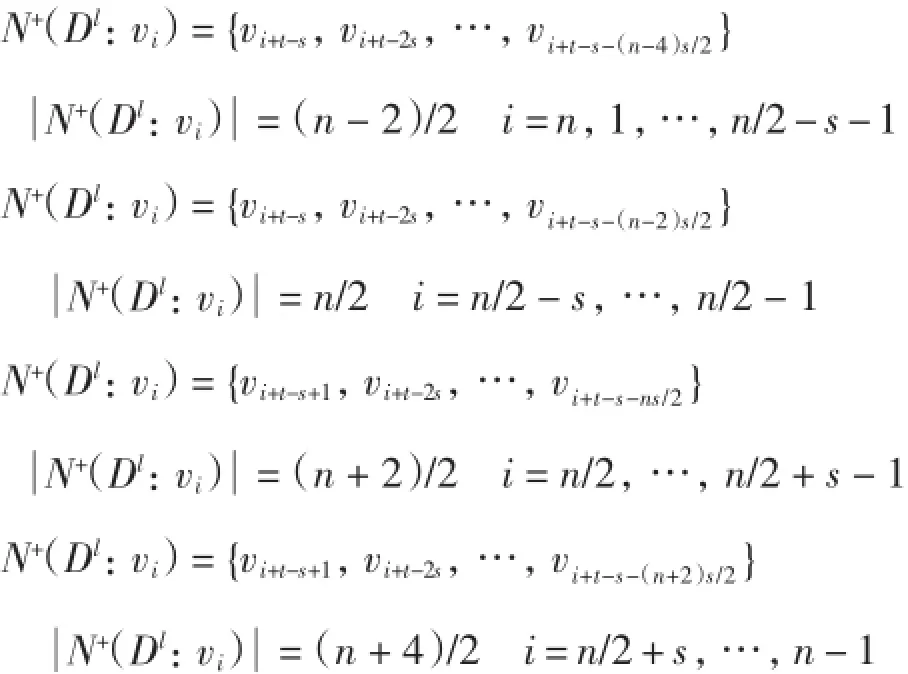
由此可得：

当 i=n/2+s，…，n-1，j=1，…，n时，有N（+Dl：vi，vj） ≥（n+4）/2+（n-2）/2-n=1，k（D：vi，v）j≤l；

当i=n/2，…，n/2+s-1，j=n/2-s，…，n/2+s-1时，有 N（+Dl：vi，v）j≥（n+2）/2+n/2-n=1，k（D：vi，v）j≤l；

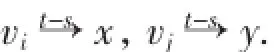
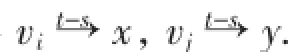
所以对任意u、v∈V（D），均有k（D：u，v）≤t-s+ （s-1）n/2.

下面证明k（D）≥t-s+（s-1）n/2.因为

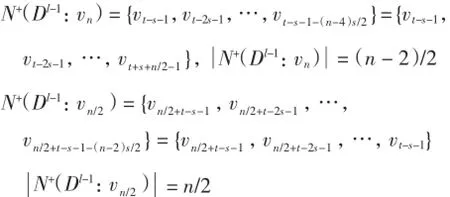
综上所述，k（D）=t-s+（s-1）n/2.定理得证.

参考文献：

［1］AKELBEK M，KIRKLAND S.Coefficients of ergodicity and scrambling index［J］.Linear Algebra and Its Applications，2009，430（4）：1111-1130.

［2］ AKELBEK M，KIRKLAND S.Primitive digraphs with the largest scrambling index［J］.Linear Algebra and Its Applications，2009，430 （4）：1099-1110.

［3］AKELBEK M，FITAL S，SHEN J.A bound on the scrambling index of a primitive matrix using Boolean rank［J］.Linear Algebra and Its Applications，2009，431（10）：1923-1931.

［4］ LIU B，HUANG Y.The scrambling index of primitive digraphs［J］. Computers and Mathematics with Applications，2010，60：706-721.

［5］CHEN S，LIU B.The scrambling index of symmetric primitive matrices ［J］.Linear Algebra and Its Applications，2010，433（6）：1110-1126.

［6］HUANG Y，LIU B.Generalized scrambling indices of a primitive digraphs［J］.Linear Algebra and Its Applications，2010，433（11）：1798-1808.

［7］HWA K K.Scrambling index set of primitive digraphs［J］.Linear Algebra and Its Applications，2013，439（7）：1886-1893.

［8］SHAO Y L，GAO Y B，LI Z S.The m-competition indices of symmetric primitive digraphs without loops［J］.Electronic Journal of Linear Algebra，2012，23（1）：457-472．

［9］KIM H K.Generalized competition index of an irreducible Boolean matrix［J］.Linear Algebra and Its Applications，2013，438（6）：2747-2756．

［10］KIM H K，PARK S G.A bound of generalized competition index of a primitive digraph［J］.Linear Algebra and Its Applications，2012，436 （1）：86-98.

（责任编校马新光）

第一作者：宋卓蓉（1990—），女，硕士研究生.

文章编号：1671-1114（2016）01-0004-04 1671-1114（2016）01-0008-04

中图分类号：O157.5

文献标志码：A

收稿日期：2015-03-20

基金项目：国家自然科学基金资助项目（11071227）.

通信作者：高玉斌（1962—），男，教授，主要从事组合数学方面的研究.

Scrambling index of primitive digraph with one n-cycle and two s-cycles

SONG Zhuorong，GAO Yubin
（Department of Mathematics，North University of China，Taiyuan 030051，China）

Abstract：Based on the graph Ds，n，one s-cycle is added.The primitive digraph of order n with one n-cycle and two s-cycles where the two s-cycles have common vertexes is studied.By analyzing the vertex set of each vertex in digraph can be reached by a walk of length t，the scrambling index of such primitive digraph is obtained.

Keywords：primitive digraph；scrambling index；cycle