基于三维CAD模型的复杂艏、艉船型曲面快速光顺方法及实现
周春凯,董枫,罗亮,陈顺怀,廖显庭
1中国舰船研究设计中心,湖北武汉4300642武汉理工大学交通学院,湖北武汉430063
基于三维CAD模型的复杂艏、艉船型曲面快速光顺方法及实现
周春凯1,董枫2,罗亮2,陈顺怀2,廖显庭1
1中国舰船研究设计中心,湖北武汉430064
2武汉理工大学交通学院,湖北武汉430063
利用船舶型值和复杂艏、艉特征参数等数据,结合三维CAD设计软件进行初步建模,提出一种基于三维CAD软件模型的复杂艏、艉船型曲面快速光顺方法,实现复杂艏、艉船型曲面的快速三向光顺。利用生成的光顺仿真模型和曲面求交算法,获得艏、艉部位任意型值点数据。该方法将拼接和光顺处理分为三个阶段来实现,即曲面重建、G1光顺拼接、曲面微调3个阶段。相较于三维CAD软件中基于单个控制点调整的曲面拼接光顺方法,该方法能够大幅提高曲面拼接与光顺的处理效率,同时曲面的内在连续性和型值点数据精度也得到了保证。
三维CAD模型;复杂艏、艉;船型曲面;拼接;光顺
网络出版地址:http://www.cnki.net/kcms/detail/42.1755.TJ.20160729.0945.004.html期刊网址:www.ship-research.com
引用格式:周春凯,董枫,罗亮,等.基于三维CAD模型的复杂艏、艉船型曲面快速光顺方法及实现[J].中国舰船研究,2016,11(4):7-13.
ZHOU Chunkai,DONG Feng,LUO Liang,et al.Fast fairing method for ship-hull surfaces with complex bow and stern based on 3D models[J].Chinese Journal of Ship Research,2016,11(4):7-13.
0 引 言
目前,在三维CAD设计软件中进行的船舶型线设计,主要是通过将船舶各分段对应的型值点转化为全船坐标点,再将全船坐标点生成样条曲线,然后由样条曲线生成NURBS曲面模型,由此进行船舶型线设计和总体性能计算。然而,在型值表中的这些离散型值点并不能够完全有效地表达整个船体线型。型值点缺乏数据不仅在三维设计软件建模过程中容易引起曲面片之间的较大孔洞和缝隙,使曲面拼接工作量大为增加,而且造成复杂艏、艉形状与船舶主体的连接往往不光顺,进一步加大了曲线、曲面光顺的工作量。同时,在船舶CAD/CAE软件的三维建模过程中,对于复杂艏、艉船型曲面,其曲面曲率变化剧烈,仅根据型线图中提供的有限站位处的型值点无法建立光顺和精确的复杂艏、艉三维模型。三维模型的不光顺不仅造成三维CAD设计软件自动生成的二维型线图不光顺,也容易引起总体性能计算结果的偏差。
另一方面,在船舶复杂艏、艉船型多方案优化设计中,设计人员需要不断将光顺后的复杂艏、艉船型数据导入到CAD/CAE三维设计软件中进行艏、艉选型设计和优化。在三维设计软件中建立光顺的三维模型时,由于需要通过手工交互调节曲线曲面的控制点不断地进行曲线曲面的拼接和光顺才能实现,调节过程异常繁杂,工作量大,计算和分析效率低,严重制约了船舶型线设计和复杂艏、艉多方案选型与优化的效率。
有鉴于此,本文利用船舶型线设计所必需的型值和复杂艏、艉特征参数等相关数据,结合三维设计软件进行初步建模和型线设计。通过导出IGES文件提取三维模型数据,并采用曲线曲面拼接与光顺算法[1-2]等处理技术,避免频繁地手工交互调整控制点,自动快速实现船舶复杂艏、艉三维模型的光顺。利用生成的三向光顺仿真模型,采用曲面求交算法获得船体肋位以及复杂艏、艉部位的任意横剖面处型值点的数据,而且,通过相应的IGES数据接口的研究开发,可以快速将生成的船舶和复杂艏、艉外型三维光顺仿真模型及型值数据导入到其他CAD/CAE软件中以进一步完成模型处理和仿真分析,大幅提高复杂艏、艉船型三维建模的效率,减少大量、繁琐的数据重复输入,从而快速有效地进行复杂艏、艉的设计和优化,为复杂艏、艉的型线设计研究和总体性能预估等提供技术支撑。
1 曲面拼接光顺算法理论分析
1.1曲面拼接理论及算法原理
船体曲面特别是艏、艉曲面由轮廓复杂和不规则的三维曲面构成,在三维CAD设计软件系统中,试图用一张曲面去构造其几何模型极难保证模型精度,因此,需要将船体曲面划分为多个比较简单、容易处理的曲面片,根据实际的光滑性要求对这些曲面片进行拼接和缝合,最终完成船体曲面设计,实现船体的整体几何造型。曲面拼接和光顺是曲面设计的两项基本工作,两者具有理论交叉,拼接的本质是使邻接的曲面片在边界处具有满足设计要求的光顺性。衡量拼接质量的一个重要因素就是光滑性,而光滑性的高低取决于拼接曲面边界的连续性。
两块B样条曲面的G1拼接算法[3-4]适用于边界完全重叠的情况,也适用于不完全重叠的情况,如图1所示。给定两B样条曲面 p(s,t)和q(u,v),其控制顶点网格分别为(i=0,1,…, m1;j=0,1,…,n1),(i=0,1,…,m2;j=0,1,…, n2);参数s与t的次数为 k1与l1,两个节点矢量与;参数u与v的次数为k2与l2,两个节点矢量与。对于G0连续的两曲面 p(s,t)与q(u,v)上的公共边界点Qj,有Qj=p(s′,0)=q(u′,1)。s′和u′分别为节点矢量S和U中对应Qj的参数值,pt(s′,0),qv(u′,1),qu(u′,1)分别为点Qj处跨界切向矢量。两曲面在Qj处具有公共的切平面的条件如式(1)所示。
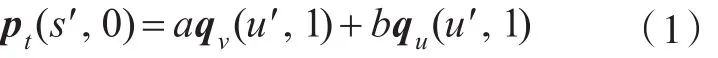
式中:a与b为常数。另外为保证两曲面在该点处不形成尖棱,应满足a>0。
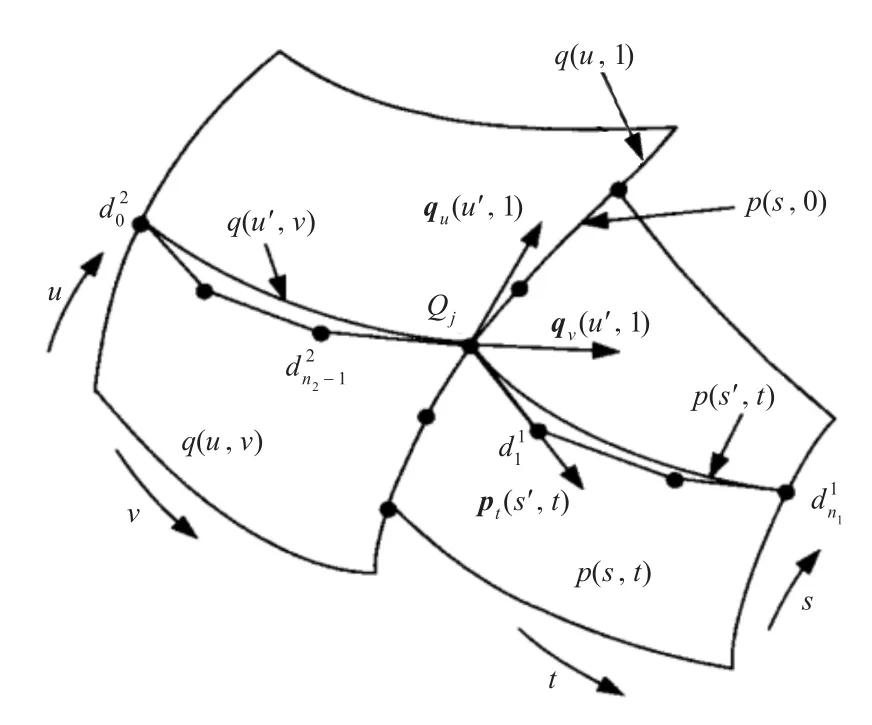
图1 B样条曲面的G1拼接Fig.1 G1-splicing of B-spline surface
两曲面在点Qj处的等参数线可表示为
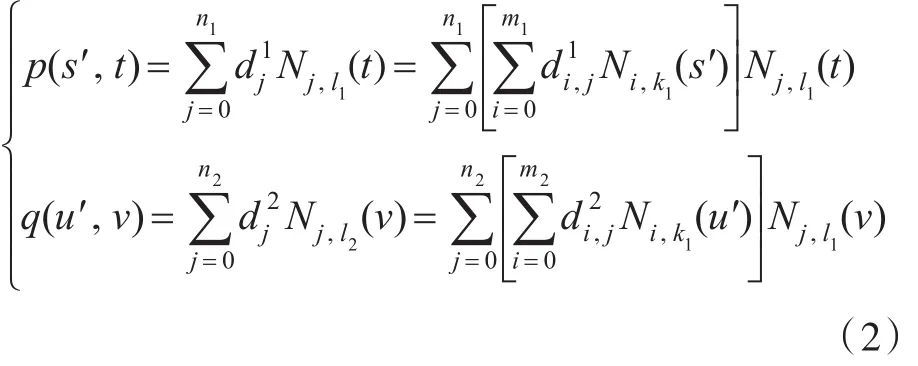
式中,Nj,l(t)为B样条基函数,其余类似符号与此
1意义相同。根据B样条曲线的端点性质,有Qj==成立,且两曲面在Qj处的跨界切向矢量分别为
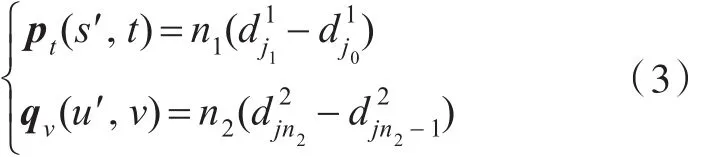
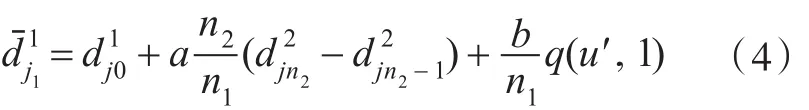
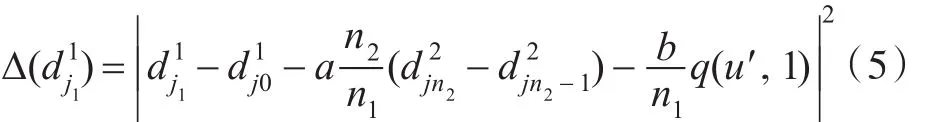
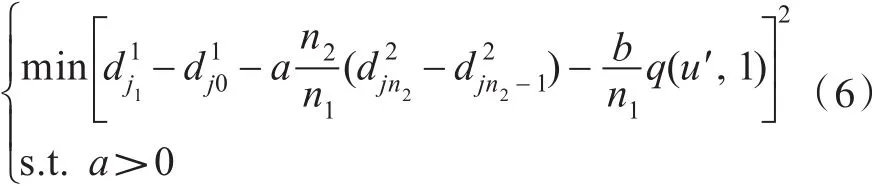
求解式(6)可以使用拉格朗日乘子法,得到a 与b,再代入式(4),便可得到调整后的控制顶点dˉ1j1。对于B样条曲面p(s,t)上等参数线p(s′,t)的第i0个控制顶点,见式(2),当s′从0连续变化到1时所形成的曲线C(s)就是由曲面 p(s,t)第i0列控制顶点定义的k1次B样条曲线,数学表达式为
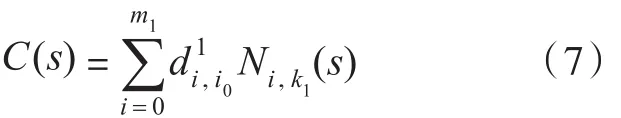
两个B样条曲面间G1光滑拼接的算法描述如下:
1)以预先给定的份数N分割参数s的定义区间,获得节点序列。
2)循环i=0,1,…,N,由式(7)获得序列{Sˉ}中Sˉ处t参数线的第1个(以0为起点)控制顶点。同时判断该位置是否位于两边界线的重合范围,由此可由式(4)得到调整后的。
重复上述步骤,可使 p(s,t)与q(u,v)达到近似的G1连续。
如果想进一步简单处理,即避开式(6)定义的优化问题,可在步骤(2)中取a=1,b=0。
1.2曲线光顺理论及算法原理
光顺准则为曲率变化均匀,即曲线具有光滑的曲率梳。
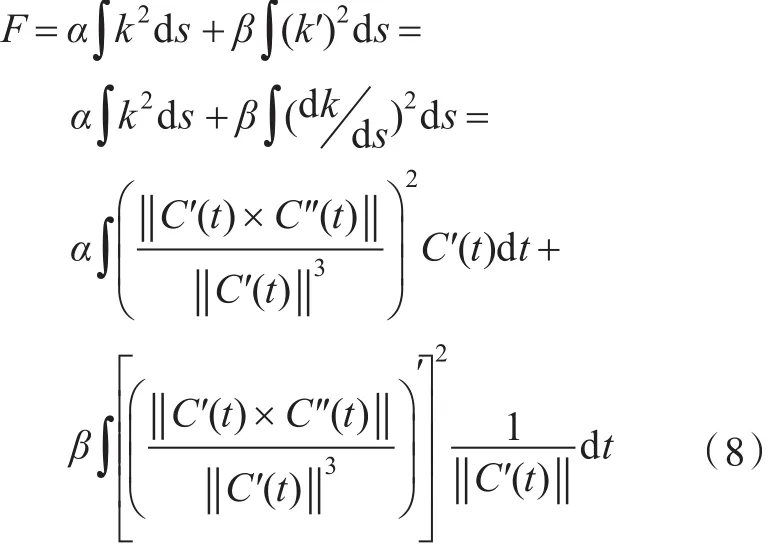
由于关注的是均匀的曲率变化,因此这里将曲率k和曲率导数k′=dk/ds作为判断的光顺依据,因此曲线C(t)的光顺性泛函为式中:第1项表征应变能,控制曲线的总曲率,第2项表征曲率导数,控制曲线的曲率变化;α和β为平衡权因子,α+β=1,控制光顺的侧重点;C′(t)和C″(t)分别为曲线C(t)的一阶和二阶导数。
光顺算法[5-9]以式(8)为目标函数,约束条件为设计者指定的控制顶点或型值点偏离,包括切向矢量和法向矢量等约束条件,令光顺前后的曲线分别为C0(t)和C(t),则约束条件相应的表达式分别为:
针对正算问题,控制顶点偏离:
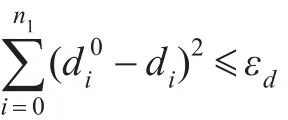
针对插值问题,型值点偏离:
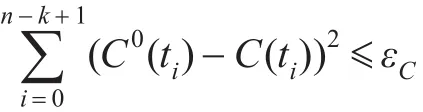
切向矢量约束:
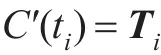
法向矢量约束:
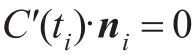
在构造了光顺性泛函和约束条件后,便可通过相应的优化问题得到光顺优化后的曲线。
2 曲面快速拼接光顺算法实现
2.1船型曲面拼接光顺整体研究流程
利用船舶型值和复杂艏、艉特征参数等数据,结合三维CAD设计软件进行初步建模和型线设计,采用曲面拼接和曲线曲面光顺算法,进行复杂艏、艉船型的快速三向光顺。利用生成的光顺模型,采用曲面求交算法可以获得复杂艏、艉曲面任意型值点的数据,相应的数据接口可以快速将复杂艏、艉船型三维光顺模型数据转换成.iges文件格式,导入到CAD/CAE软件中进行进一步的模型处理和仿真分析,从而提高复杂艏、艉船型的优化设计效率。整体研究流程如图2所示。
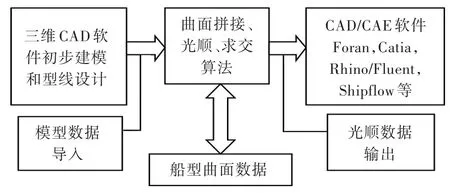
图2 整体研究流程Fig.2 The process of whole research for fairing
2.2曲面快速拼接、光顺的具体实施方案
曲面的快速拼接光顺处理分为3个阶段,在这3个阶段之前称为预处理阶段,即还需要经过曲线的光顺处理,主要是对一些边界曲线进行快速光顺处理,参见1.2节。
第1阶段:曲面重新生成。使具有共同边界的各曲面在拼接处具有相同数目的控制顶点,同时在相应的方向具有相同的次数,这一阶段因为所有的曲面皆为双三次所以可自动满足。在此阶段可以通过三维设计软件Foran中的reinterpolate命令或者用Rhino的曲面重建命令实现,其他如CAD/CAM软件也基本包含类似功能。在处理过程中曲面形状可能会发生变化,但是只要给定适当数量的u向和v向的控制顶点数,便可以较好地达到保形的要求。
第2阶段:曲面G1光滑拼接。这部分内容参见第1.1节的拼接算法实现过程。
第3阶段:各曲面内部调整。保持边界和G1连续性条件。
船型曲面需要满足船舶的设计要求,本文采用一种保持边界和G1连续性的曲面全局调整方法来调整曲面,让设计者交互地调整曲面,从而最终获得较为光顺的曲面。该方法虽然依旧为交互式调整,但由于每次能大范围调整,大幅减少了设计工作量,极大提高了复杂曲面的拼接光顺效率。
具体的调整方法分为两种:一种为双线性调整,另一种为双余弦调整。两者流程基本一致,具体步骤如下:
1)获得曲面的u向和v向控制顶点数m和n,如图3所示。图中的方格点即为曲面的控制网格。注意这里只调节曲面控制顶点的y坐标分量,图中为控制顶点的拓扑结构图,而非实际的控制顶点。
2)设计者根据曲面具体的凹凸情况选择调整峰值点,即调整幅度最大的点,如图3中的红色点所示,调整的幅值r也由设计者给定。具体的幅值可参考该曲面和周围邻接曲面的匹配情况。以艏部曲面为例,对于拓扑为6×12的曲面,由于其相对周围邻接曲面凸起明显,因此幅值可取得较大一些,例如0.1或0.2。通常幅值建议取小一些,这样能够更容易掌握曲面的整个细节变化过程。
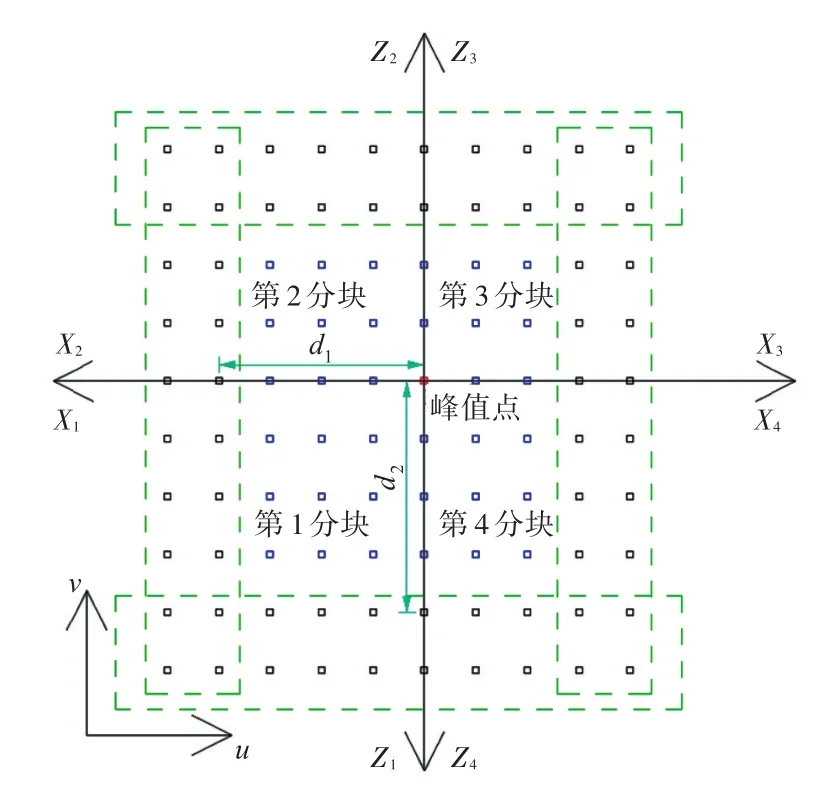
图3 单片曲面分块示意图Fig.3 Division of single patch
3)为了保持边界和与其他曲面间的G1连续性条件,需要保证艏、艉两行和艏、艉两列的控制顶点不变,需调整的点仅包括中间的蓝色方格点和红色峰值点。
4)以峰值点为坐标原点,将需调整的点分为4个分块,每个分块采用相应的双线性函数或双余弦非线性函数进行调整。函数的确定方式要保证在峰值点处函数取得极大值,同时保证函数在紧邻最外层的那一层控制顶点处取得极小值,即调整值为0。以第1分块为例,双线性函数和双余弦函数分别为:
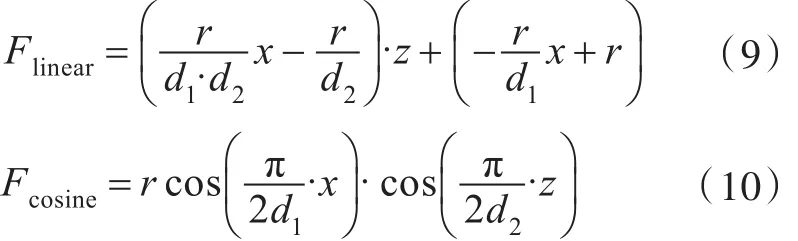
式中:d1为峰值点到该分块与边界控制顶点相邻的那一列控制顶点间的x向距离;d2为峰值点到该分块与边界控制顶点相邻的那一行控制顶点间的z向距离。其他3个分块的调整函数确定方式与第1分块类似。
5)输出调整后的曲面。第3阶段的流程如图4所示。
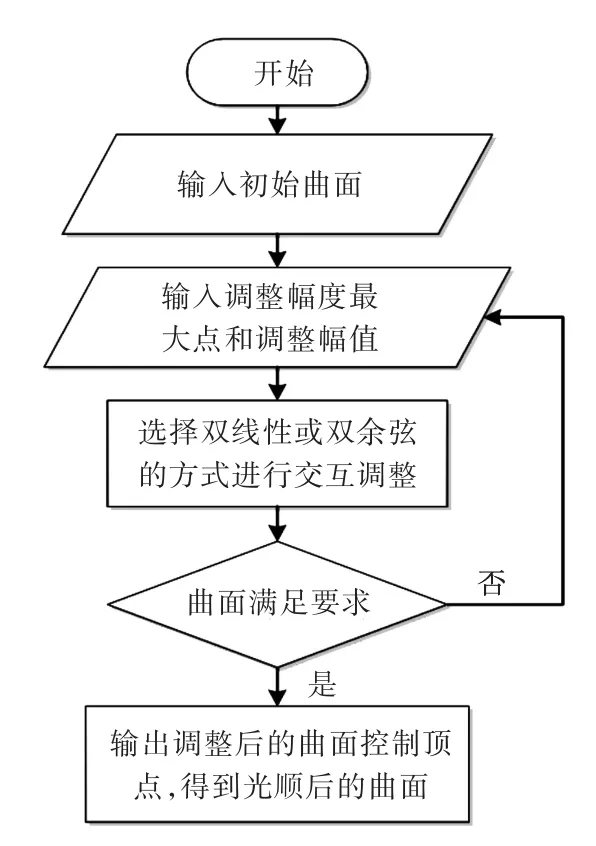
图4 曲面微调流程Fig.4 The process of surface fine-tuning
3 算法测试与数据对比分析
3.1第1阶段前后对比
以某大型拖网渔船艏部曲面为例(艉部曲面的处理与此相同),分析3个阶段的前后数据对比。第1阶段为曲面重建,使共边界曲面在边界处具有相同数量的控制顶点。通过对比,重建后的曲面完全达到了保形要求,而且还消除了部分曲面褶皱,但独立曲面片之间的不连续性依旧非常明显,如图5所示。

图5 重建前、后曲面对比图Fig.5 Comparison of surface before and after reinterpolation
3.2第2阶段前后对比
G1拼接前的曲面即为重建后的曲面,如图5(b)所示,图6则为G1拼接后的曲面。从G1光滑拼接前后对比,可明显地看到曲面在拼接处光顺性的改善,且从图7所示的等照度线图对比中也可证明各曲面片确实达到了近似G1连续。

图6 G1拼接后曲面图Fig.6 Surface after G1-splicing

图7 G1拼接前、后等照度线对比图Fig.7 Comparison of surface's isophotes before and after G1-splicing
3.3第3阶段前后对比
分析上一阶段得到的艏部曲面,发现连接球艏和进流段大曲面的曲面片在内部有些不必要的凸起,因此调整该曲面,将行数为8,列数为4的控制顶点作为修改的峰值点,调整幅值为0.1 m,仅经过几次的双线性和双余弦调整后的曲面对比如图8和图9所示。从图中可以明显看出调整后的曲面大幅地削弱了该凸起面的凸起情况,调整后的曲面要明显优于调整前的曲面。由于可以实时显示曲面的投影等值线,因此仅通过几次调整便达到了所期望的较好效果,相对于之前的单点调整,大幅提高了光顺修改效率。
3.4精度验证

图8 微调前后主视图对比Fig.8 Comparison of surface's front view before and after fine-tuning
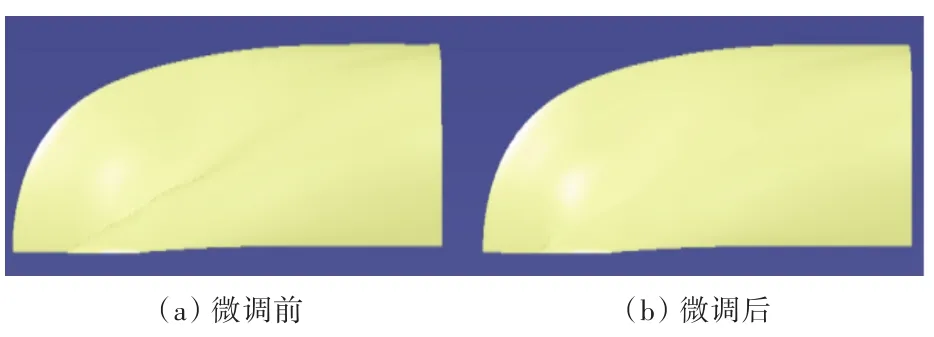
图9 微调前后俯视图对比Fig.9 Comparison of surface's plan view before and after fine-tuning
以19.5站为例,分析拼接光顺处理前后的精度偏差。表1列出了处理前和处理后的曲线与原插值曲线的型值点偏差值,型值点数据通过基于二维标量场抽取等值线的平面与曲面求交算法[10-12]获得,确保不会漏交。由于站线是横向曲线,因此这里只列出了y方向的偏差值。从表中可以看出处理后要比处理前的偏差小得多。
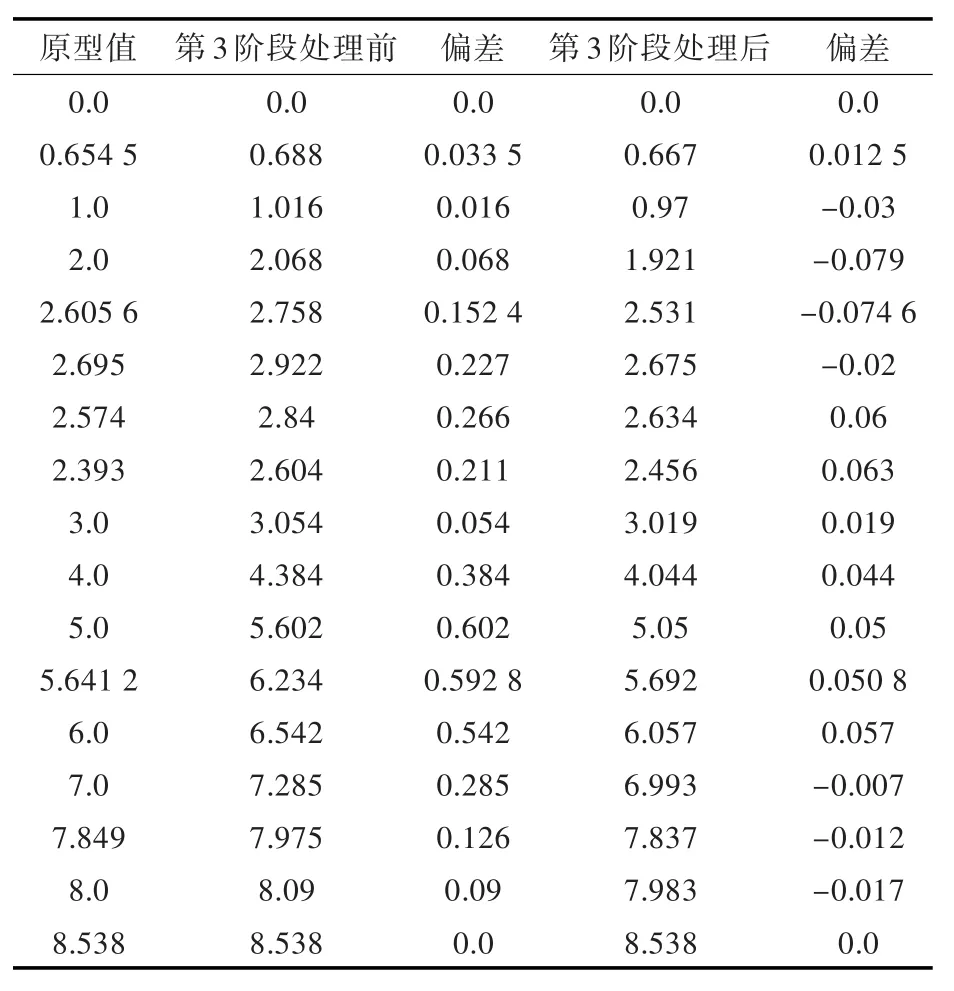
表1 处理前后19.5站曲线与原曲线型值点偏差Tab.1 Relative errors of 19.5 station curve before and after splicing and fairing
3.5运行时间
第1阶段可以直接在三维CAD设计软件上执行,运行时间较快,只要点击相应命令即可瞬间完成。第2阶段通过执行优化函数来完成保形的G1拼接,由于需要处理大量的矩阵和优化问题,因此这个过程耗时最多,针对艏部曲面大概需要3~5 min。第3阶段本质上是一个人工交互过程,但是该过程通过用偏离函数来对整个控制顶点拓扑进行变形,因此,相较于每次只调整一个控制点,会节约大量的时间,艏部实例第3阶段耗时约需几分钟。显然,这要比在三维CAD软件中进行单点光顺调整的效率高得多。
4 复杂艏、艉船型快速光顺系统
4.1曲线光顺系统界面
复杂艏、艉船型曲面快速拼接光顺系统的编写以MATLAB的图形用户界面GUI为平台[13]。图10所示为艏轮廓边界曲线的光顺实例界面图,其中控制顶点容许偏差取为0.5。在该界面中,第1个坐标系是用来表示导入和修改的曲线,第2个坐标系是用来进行人工交互的界面。该系统可以对曲线进行快速光顺,显示曲线的控制顶点和曲率图等功能。
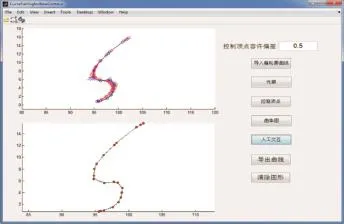
图10 艏轮廓边界曲线光顺界面Fig.10 The interface of fairing for bow's profile curve
4.2曲面拼接和微调系统界面
图11所示为艏部曲面的光顺拼接和微调界面,在该界面中,坐标系是用来表示导入和修改的曲面,设计者可实时观测修改后的曲面以及相应的Z向投影等值线(即水线),以便更直接地判断曲面的修改趋势。该系统软件首先能够对曲面进行G1拼接光顺,然后可以对曲面控制顶点进行线性和非线性(余弦)的微调,同时能够读取曲面的控制网格,显示在右侧的3个表格中。如图11所示,控制顶点偏差取0.1,调整曲面编号为5,即凸起最大的那片连接球艏和主船体之间的曲面,峰值点为8行、4列的控制顶点。
图12所示为艉部曲面的光顺微调界面,其中控制顶点偏差取0.1,调整曲面编号为4,即连接艉封板和主船体之间的曲面,峰值点为5行、30列的控制顶点。
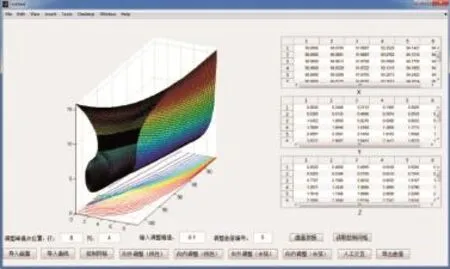
图11 艏部曲面调整实例Fig.11 The interface of fairing for bow's surface
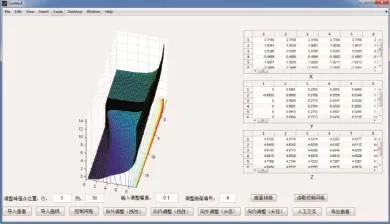
图12 艉部曲面调整实例Fig.12 The interface of fairing for stern's surface
5 结 语
本文深入研究了船体曲面的拼接和光顺处理问题,提出了一种基于三维CAD软件模型的复杂艏、艉船型曲面快速光顺方法,将拼接和光顺处理分为3个阶段来实施:曲面重建;G1光顺拼接;曲面微调。相较于三维CAD软件中传统的单个控制点调整方法,本方法能够极大地提高曲面光顺修改效率,同时曲面的内在连续性和型值点数据精度也得到了保证。
本方法的不足之处在于第3阶段依旧是一个人工交互过程,尽管提高了效率,但还是比较依赖于设计者的实际经验。如何进一步实现复杂曲面光顺处理的全自动化,是今后研究的方向。
[1] 程少华,吴华.两相邻3次B样条曲面G1连续充分条件[J].河南师范大学学报(自然科学版),2006,34 (3):48-50.
CHENG Shaohua,WU Hua.G1continuity between two patches of adjacent cubic B spline surface[J].Journal of Henan Normal University(Natural Science Edition),2006,34(3):48-50.
[2]CHE X J,LIANG X Z.G1continuity conditions of B-spline surfaces[J].Northeastern Mathematical Journal,2002,18(4):343-352.
[3] 李旭.双三次NURBS曲面拼接及光顺的研究与实现[D].西安:西安理工大学,2007:18-20.
[4]曲学军,宁涛,席平.B样条曲面的光滑拼接[J].计算机辅助设计与图形学学报,2004,16(1):138-141.
QU Xuejun,NING Tao,XI Ping.Smooth joining between adjacent B-spline surfaces[J].Journal of Computer Aided Design&Computer Graphics,2004,16 (1):138-141.
[5]朱心雄.自由曲线曲面造型技术[M].北京:科学出版社,2000.
[6]穆国旺,涂侯杰,雷毅,等.参数三次B样条曲线的一种整体光顺方法[J].工程图学学报,1998(1):28-34.
MU Guowang,TU Houjie,LEI Yi,et al.A global fairing method for cubic B-spline curves[J].Journal of Engineering Graphics,1998(1):28-34.
[7] 穆国旺,宋秀琴,臧婷.一种选点法和能量法相结合的曲线光顺方法[J].工程图学学报,2005(6):118-121.
MU Guowang,SONG Xiuqin,ZANG Ting.A curve fairing method mixing bad points selection with energy minimization[J].Journal of Engineering Graphics,2005(6):118-121.
[8]KJELLANDER J A P.Smoothing of cubic parametric splines[J].Computer-Aided Design,1983,15(3):175-179.
[9]SAPIDIS N,FARIN G.Automatic fairing algorithm for B-spline curves[J].Computer-Aided Design,1990,22(2):121-129.
[10] 仵大伟,林焰,纪卓尚.船体曲面的NURBS表达与设计[J].大连理工大学学报,2002,42(5):569-573.
WU Dawei,LIN Yan,JI Zhuoshang.Ship hull surface's NURBS representation and design[J].Journal of Dalian University of Technology,2002,42(5):569-573.
[11] 张明霞,纪卓尚,林焰.NURBS曲面与隐式曲面求交的计算机实现及应用[J].中国造船,2002,43 (3):94-98.
ZHANG Mingxia,JI Zhuoshang,LIN Yan.Implementation and application of intersection between NURBS-based surface and implicit surface[J].Shipbuilding of China,2002,43(3):94-98.
[12] 宋宏勋,韩毅,吴初娜.一种基于等值线法的NURBS曲面与平面的求交算法[J].数字技术与应用,2011(7):103-105.
SONG Hongxun,HAN Yi,WU Chuna.An intersection algorithm of NURBS surface and plane based on the method of isoline[J].Digital Technology&Application,2011(7):103-105.
[13] HANSELMAN D,LITTLEFIELD B.精通MATLAB综合辅导与指南[M].李人厚,译.西安:西安交通大学出版社,1998.
Fast fairing method for ship-hull surfaces with complex bow and stern based on 3D models
ZHOU Chunkai1,DONG Feng2,LUO Liang2,CHEN Shunhuai2,LIAO Xianting11 China Ship Development and Design Center,Wuhan 430064,China
2 School of Transportation,Wuhan University of Technology,Wuhan 430063,China
Based on the point net of offset and complex ship-hull parameters,using preliminary surface models made by 3D CAD software,this paper presents a fast fairing method for ship-hull surface modelling with complex bow and stern based on 3D models.With fairing simulation 3D-models and the surface intersection algorithm,the fairing point net of offset for arbitrarily complex bow and stern of ship-hull surfaces is first obtained.The method then divides the splicing and faring process into three stages:surface reinterpolation,G1-splicing,and surface fine-tuning.In contrast to traditional splicing and faring method based on a single control point of surface,this method improves the efficiency of surface's splicing and faring greatly,while the interior continuity of the surface and the precision of the offset points can be guaranteed. Key words:3D CAD models;complex bow and stern;ship-hull surfaces;splicing;fairing
U622.9
A
10.3969/j.issn.1673-3185.2016.04.002
2015-10-23网络出版时间:2016-7-29 9:45
中国舰船研究设计中心研发基金资助项目
周春凯(通信作者),男,1973年生,硕士,高级工程师。研究方向:舰船总体设计与信息化技术。E-mail:zhouoldk@126.com
董枫,男,1988年生,博士生。研究方向:船舶CAD设计
——福船

