基于超松弛解析迭代方法的多导体传输线电磁脉冲响应计算方法
郭俊,李妮,张建功,谢彦召
1西安交通大学电气工程学院,陕西西安7100492电力设备电气绝缘国家重点实验室,陕西西安7100493中国电力科学研究院,湖北武汉4300744电网环境保护湖北省重点实验室,湖北武汉430074
基于超松弛解析迭代方法的多导体传输线电磁脉冲响应计算方法
郭俊1,2,李妮3,4,张建功3,4,谢彦召1,2
1西安交通大学电气工程学院,陕西西安710049
2电力设备电气绝缘国家重点实验室,陕西西安710049
3中国电力科学研究院,湖北武汉430074
4电网环境保护湖北省重点实验室,湖北武汉430074
电磁脉冲会在多导体传输线中感应出较高幅值的感应电压和电流,对传输线端接设备等具有严重威胁。所以,对多导体传输线进行建模,分析多导体传输线电磁脉冲响应对于预测电力线的电磁脉冲效应,研究其保护方法具有重要的意义。在多导体传输线建模方面,传统的链参数矩阵算法由于存在大量的矩阵求逆运算,在存在大量线缆时其计算速度较慢。基于此问题,提出了基于解析迭代方法的多导体传输线电磁脉冲响应计算方法(DARIT-field),该方法在求解每根线缆上的响应时,将临近线缆的串扰耦合效应等效为在临近线缆上均匀分布的激励源,计算过程得到了大幅简化。并对基于不同迭代方法的多导体传输线电磁脉冲响应计算方法进行了对比,最后利用实例对每种方法的优、缺点进行了对比。
解析方法;电磁脉冲;迭代方法;暂态分析;传输线模型;波形松弛
0 引 言
高空核爆电磁脉冲(HEMP)一般由爆高在30 km以上的核爆炸产生,其中的E1成分频谱覆盖范围包括中频、高频、甚高频甚至一些超高频波段的信号,具有辐射范围广,峰值场强高和频谱宽的特点[1-5],会在舰船上的多导体传输线上耦合感应出幅值较高的感应电压和电流,严重威胁到传输线终端端接的各类负载设备[6-16]。因此,多导体传输线电磁脉冲响应建模计算对于舰船电磁脉冲响应评估具有重要意义。
传统的对多导体传输线电磁脉冲响应计算方法是链参数矩阵算法,该算法通过对传输线电报方程矩阵进行相模变换求解,可以准确地得到线缆中的响应电压和电流。但由于多导体传输线中所有线缆都存在串扰耦合效应,该方法在计算过程中需要进行大量的矩阵求逆运算来进行解耦,计算效率低下。为了应对这一问题,基于解析迭代算法的多导体传输线电磁脉冲响应计算方法(DARIT-field算法)是较好的解决方法[17]。该算法利用解析迭代的方法来对传输线电磁脉冲响应进行计算,该方法在求解每根线缆上的响应时将临近线缆的串扰耦合效应等效为临近线缆上分布的激励源,而在求解过程中采用迭代的方法进行逐步求解。在第一步迭代时,只考虑电磁波对各线缆的作用,而从第二步迭代开始,将考虑线缆之间的串扰效应。相比传统算法,其计算效率大幅提高。但是,以往的DARIT-field算法都是基于Jacobi迭代以及Gauss-Seidel迭代等传统迭代方法。而从迭代方法来说,Jacobi迭代和Gauss-Seidel迭代方法分别是超松弛迭代方法JOR迭代和SOR迭代方法的特殊情形。在JOR迭代和SOR迭代中的松弛因子等于1的情况下,此两种迭代方法就分别等于Jacobi迭代和Gauss-Seidel迭代方法。而当松弛因子等于最佳值时,JOR算法或SOR算法可能会具有相比Jacobi迭代和Gauss-Seidel迭代更高的收敛速度[18]。本文将提出一种基于超松弛迭代的多导体传输线电磁脉冲响应解析迭代算法,并将该算法与基于传统迭代的算法进行对比。
1 理 论
所研究的场线耦合问题如图1所示。
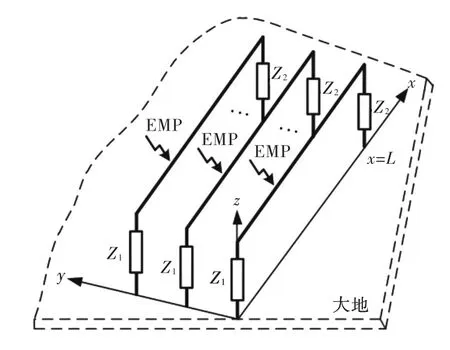
图1 多导体传输线结构示意图Fig.1 The configuration of the MTLs model
如图1所示,多导体传输线由N根导线组成,长度为L,导体两端均端接线性负载。所有导体均处于电磁脉冲的辐照之下,在计算中,首先将电磁脉冲激励变换到频域,对每一个频率下的响应进行求解,最后再将其响应变换到时域即可得到传输线两端的电压和电流的时域响应结果。频域下多导体传输线的电报方程矩阵形式如下:
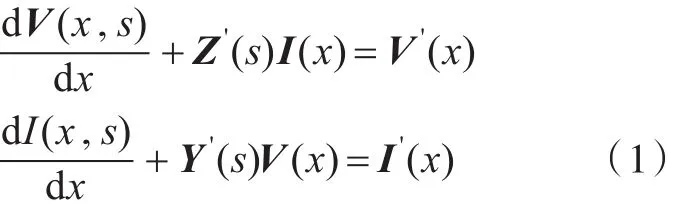
式中:V(x,s)为传输线的沿线电压矩阵;I(x,s)为传输线沿线电流矩阵;Z'为传输线的波阻抗矩阵;Y'为传输线的导纳矩阵;s为拉普拉斯算子。
将方程写为离散形式,则第i根导线的电报方程为:j≠i
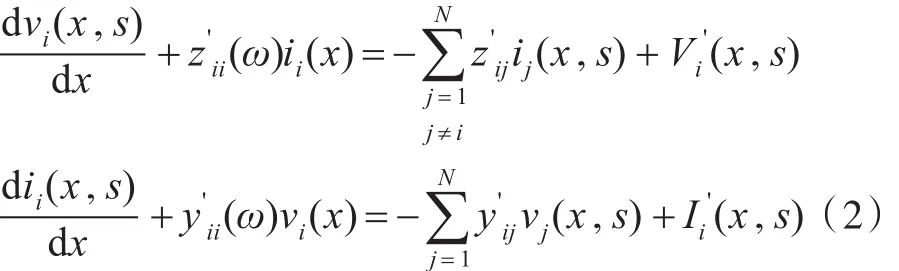
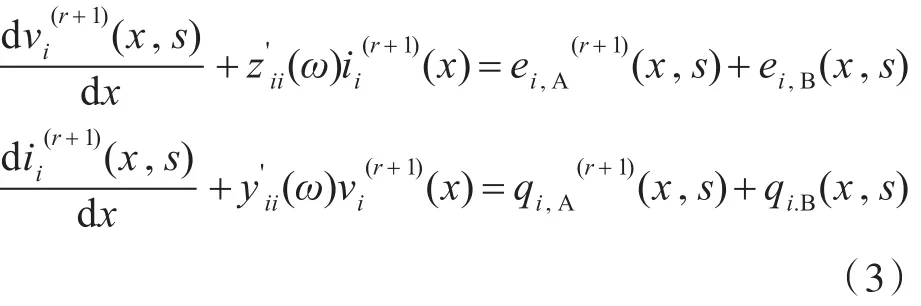
Jacobi迭代:
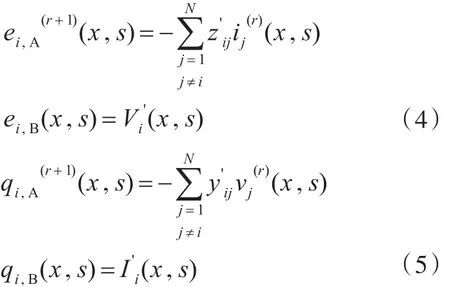
Gauss-Seidel迭代:
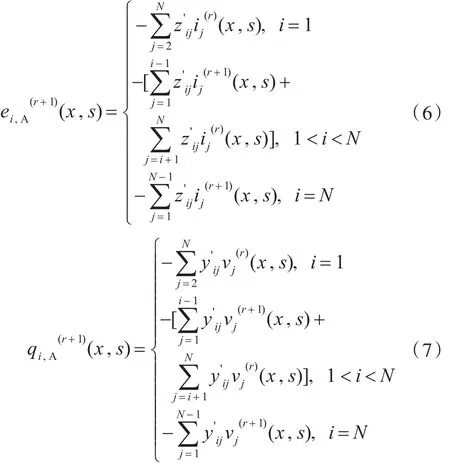
由上述方程可以看出,迭代公式等式的右边分为两部分,第一部分(A部分)为与每一步迭代后的电压和电流值有关的迭代项,第二部分(B部分)为一个常数项,其在每一步迭代中都相等。由于上述微分方程为二元一阶微分方程,为了求解,对式(3)进行如下变换:其中:
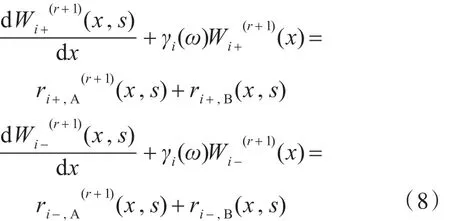
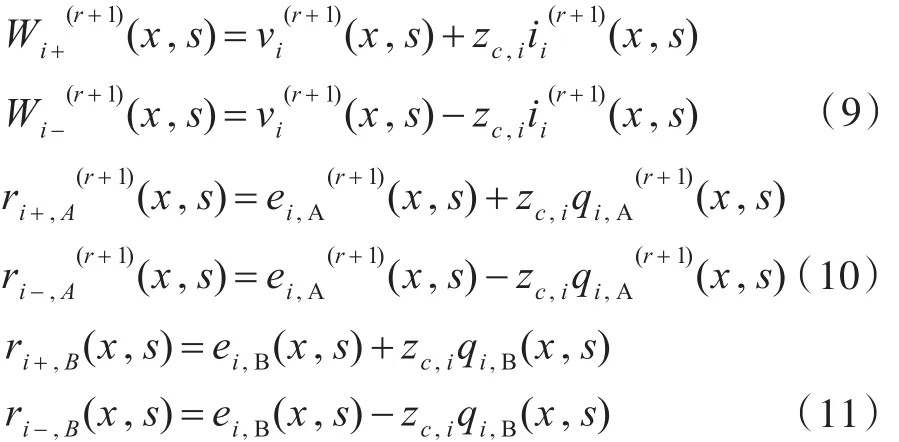
式中:zc,i为第i根传输线的特征阻抗。联立方程(8)进行求解。其初始值利用BLT方程求解,其BLT方程的源项为:
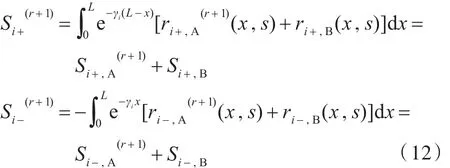
式中:γi为第i根传输线的传播因子。由式(12)可知,每一步迭代的BLT源项分为A,B两部分,A部分与每一步的电压和电流值有关,在每一步迭代中都是不同的,而B部分与外加电磁场有关,其值在每一步迭代中都相同。
JOR迭代方法和SOR迭代方法可分别由Jacobi迭代和Gauss-Seidel迭代方法扩展而来。其每一步迭代后的结果分别为基于Jacobi迭代和Gauss-Seidel迭代本步迭代和上一步迭代的加权平均,加权因子即为松弛因子。其迭代过程如下。
JOR迭代:
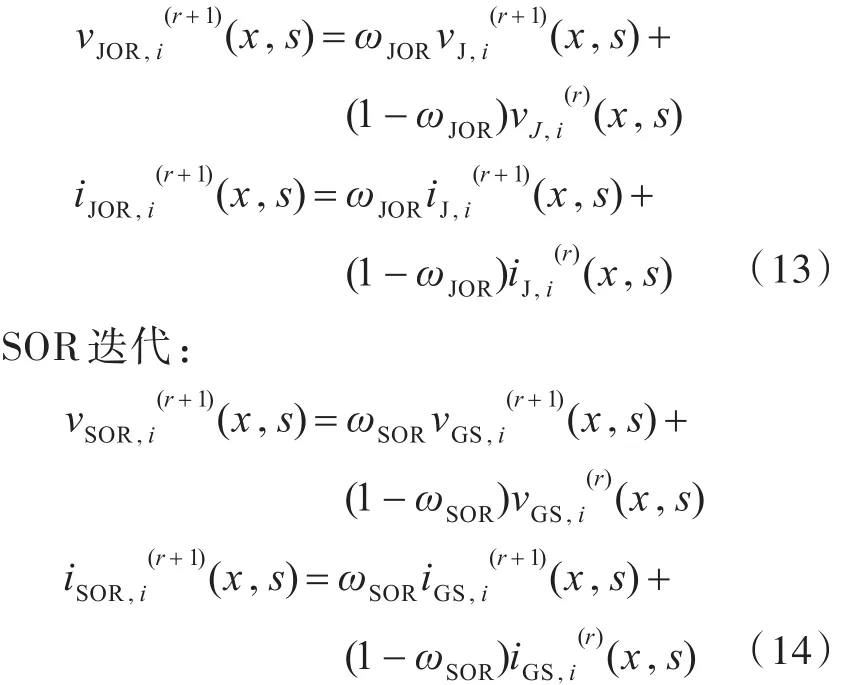
式中:ωJOR为JOR迭代中的超松弛因子;ωSOR为SOR迭代中的超松弛因子;vJOR,iJOR为JOR迭代的电压和电流计算结果;vj,ij为Jacobi迭代中的电压和电流计算结果;vSOR,iSOR为SOR迭代的电压和电流计算结果;vGS,iGS为Gauss-Seidel迭代中的电压和电流计算结果。
2 算例及模型验证
为了对基于几种不同迭代方法的多导体传输线电磁脉冲响应计算方法进行验证,本节将设置具体算例来对算法进行验证,在每种算例下,均利用4种迭代算法与常规算法进行计算,并进行对比,以说明算法的有效性。入射波形均为1996年颁布的IEC61000-2-9中所规定的标准波形,该波形为双指数波形,定义为
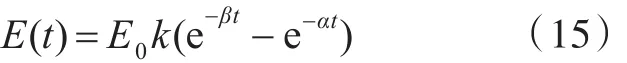
式中:E0为峰值场强,数值为50 kV/m;k为修正系数,数值为1.3;α为表征脉冲前沿的参数,数值为6.0×108s-1;β为表征脉冲后沿的参数,数值为4.0×107s-1。
考虑平行放置的3根导线,长度为0.5 m,高度为0.01 m,线缆距离为0.01 m,线缆半径为0.001 m,线缆两端端接负载均为50 Ω,地面为有损大地,其介电常数为10,电导率为0.01 S/m。电磁波入射角度为α=0°,ψ=30°,φ=0°。JOR算法的松弛因子为0.52,SOR算法的松弛因子为0.8。则经过几种算法计算后的线缆1末端电压与经过常规算法计算所得结果对比如图2所示。由图中可以看出,几种迭代算法得到的结果与传统算法均具有不同程度的一致性。几种不同算法的耗时对比如表1所示(采样点数为1 024,电脑配置为Core i5 2.8 GHz,8 GB RAM)
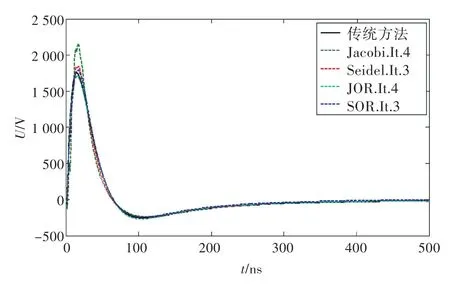
图2 线缆1末端电压迭代算法与常规算法计算结果对比图Fig.2 The far-end response of wire 1 with different methods
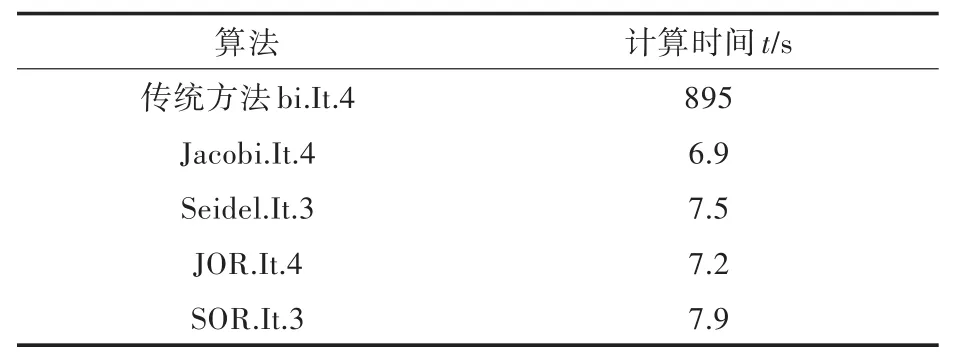
表1 计算时间的比较Tab.1 Comparison of the CPU cost
由表1可以看出,迭代方法所用时间大幅少于传统方法。
为了定量比较几种算法的精确度,引入了基于频域能量的相对误差,其定义式为
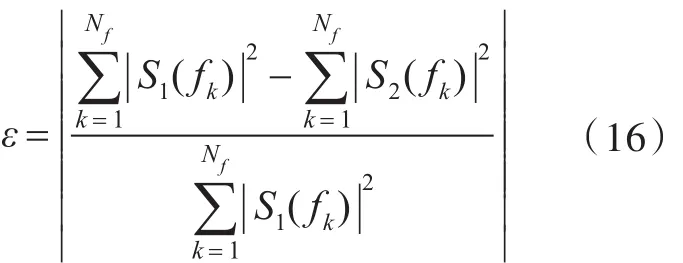
式中:Nf为计算中的采样点数;fk为波形在第k个频点的幅值;S1与S2为待比较的2个波形。本算例中频点数为512个,则几种算法的相对误差如表2所示。不同迭代步数下几种算法的相对误差如图3所示。

表2 几种算法的相对误差比较Tab.2 Relative errors of each method

图3 不同迭代步数下几种算法的相对误差Fig.3 The relative error of the four methods at different iteration steps
由表2可以看出,不同的算法其精度不同,且都随着迭代步数的增加,误差减小。相比而言,在松弛因子取值合适的情况下基于超松弛迭代的传输线响应计算方法相比传统Jacobi迭代和Gauss-Seidel迭代算法具有较好的精度。
3 结 语
本 文 分 别 对 Jacobi-DARIT-field算 法 、Seidel-DARIT-field算法、JOR-DARIT-field算法和SOR-DARIT-field算法这4种基于不同迭代方法的传输线电磁脉冲响应解析迭代算法进行了介绍。通过模型算例的验证,可知所提出的迭代方法在保证计算精度的前提下具有较高的计算效率。在几种不同迭代算法的比较中,在松弛因子取值合适的情况下,JOR-DARIT-field算法和SOR-DARIT-field算法相比Jacobi-DARIT-field算法和Seidel-DARIT-field算法具有更好的计算精度。而最佳松弛因子的选取标准则较为复杂,还需进行更深入的研究。
[1]周壁华,陈彬,石立华.电磁脉冲及其工程防护[M].北京:国防工业出版社,2003.
[2]TESCHE F M,BARNES P R.The HEMP response of an overhead power distribution line[J].IEEE Power Engineering Review,1989,9(7):80-81.
[3]许献国.美日益重视电磁脉冲威胁[J].电子技术参考,2002,2(2):59-60.
[4]SAVAGE E,GILBERT J,RADASKY W.The early-time(E1) high-altitudeelectromagneticpulse (HEMP)and its impact on the U.S.power grid[R]. California:Metatech Corporation,2010.
[5] 孙蓓云,周辉,谢彦召.两种高空核爆电磁脉冲电缆耦合效应的比较[J].强激光与粒子束,2002,14 (6):901-904.
SUN Beiyun,ZHOU Hui,XIE Yanzhao.Comparisonof the cable coupling effects under two kinds of HEMP environment[J].HighPowerLaserandParticle Beams,2002,14(6):901-904.
[6]谢彦召,王赞基,王群书,等.架空多导体传输线缆的电磁脉冲响应计算[J].清华大学学报(自然科学版),2006,46(4):449-452.
XIE Yanzhao,WANG Zanji,WANG Qunshu,et al. Calculation of HEMP coupling to aerial multi-conductor transmission lines[J].Journal of Tsinghua University(Science&Technology),2006,46(4):449-452.
[7]PAUL C R.Analysis of Multiconductor Transmission Lines[M].New York:John Wiley&Sons,2007.
[8]刘尚合,刘卫东.电磁兼容与电磁防护相关研究进展[J].高电压技术,2014,40(6):1605-1613.
LIU Shanghe,LIU Weidong.Progress of relevant research on electro-magnetic compatibility and electromagnetic protection[J].High Voltage Engineering,2014,40(6):1605-1613.
[9] MELIOPOULOS A P S,GLYTSIS E N,COKKIN IDES G J,et al.Comparison of SS-GIC and MHD-EMPGIC effects on power systems[J].IEEE Transactions on Power Delivery,1994,9(1):194-207.
[10] FOSTER J S,Jr,GJELDE E,GRAHAM W R,et al. Report of the commission to assess the threat to the united states from electromagnetic pulse(EMP)attack[R].Critical National Infrastructures,2008.
[11]TAYLOR C,HARRISON C Jr.The response of a terminated two-wire transmission line excited by a non-uniform electro-magnetic field[J].IEEE Transactions on Antennas Propagation,1965,13(6):987-989.
[12]AGRAWAL A K,PRICE H J,GURBAXANI S H. Transient response of multi-conductor transmission lines excited by a non-uniform electro-magnetic field[J].IEEE Transactions on Electromagnetic Compatibility,1980,22(2):119-129.
[13] IANOZ M,NUCCI C A,TESCHE F M.Transmission line theory for field-to-transmission line coupling calculations[J].Electromagnetics,1988,8(2/3/4):171-211.
[14]李刚,毕军建,刘尚合,等.超宽谱电磁脉冲对无线电引信的耦合及防护加固[J].强激光与粒子束,2006,18(8):1332-1336.
LI Gang,BI Junjian,LIU Shanghe,et al.Coupling mechanism between radio fuzzes and ultra band spectra electromagnetic pulse and enhancement t of radio fuzes[J].High Power Laser and Particle Beams,2006,18(8):1332-1336.
[15]RACHIDI F,NUCCI C A,IANOZ M,et al.Response of multiconductor power lines to nearby lightning return stroke electromagnetic fields[C]//Proceedings of IEEE Transmission and Distribution Conference.Los Angeles,CA,USA:IEEE,1996:294-301.
[16]TESCHE F M.On the analysis of a transmission line with nonlinear terminations using the time-dependent BLT equation[J].IEEE Transactions Electromagnetic Compatibility,2007,49(2):427-433.
[17]XIE Y Z,GUO J,CANAVERO F G.Analytic iterative solution of electromagnetic pulse coupling to multiconductor transmission lines[J].IEEE Transactions ElectromagneticCompatibility, 2013, 55(3):451-466.
[18]NAJAFI H S,EDALATPANAH S A.Iterative methods with analytical preconditioning technique to linear complementarity problems:application to obstacleproblems[J].RAIRO-OperationsResearch,2013,47(1):59-71.
网络出版地址:http://www.cnki.net/kcms/detail/42.1755.TJ.20160729.0945.038.html期刊网址:www.ship-research.com
引用格式:杜平.高隔离度和ns级响应时间的主动式射频前端限幅设计方法[J].中国舰船研究,2016,11(4):126-132.
DU Ping.A design method for high isolation and nanosecond response RF front-end active limiter module[J].Chinese Journal of Ship Research,2016,11(4):126-132.
Prediction of EMP coupling to multi-conductor transmission lines with the over relaxation analytical iterative methods
GUO Jun1,2,LI Ni3,4,ZHANG Jiangong3,4,XIE Yanzhao1,2
1 School of Electrical Engineering,Xi'an Jiaotong University,Xi'an 710049,China
2 State Key Laboratory of Electrical Insulation and Power Equipment,Xi'an 710049,China
3 China Electric Power Research Institute,Wuhan 430074,China
4 Hubei Province Key Laboratory of Power Network Environmental Protection,Wuhan 430074,China
The Distributed Analytical Representation and Iterative Technique(DARIT)is proposed in this paper for the calculation of electromagnetic pulse(EMP)radiated field coupling to multi-conductor transmissionlines(MTLs).Traditionally,thetechniqueadoptstheJacobi iterationscheme(Jacobi-DARIT-field)or the Gauss-Seidel iteration scheme(Seidel-DARIT-field).More recently,based on these two methods,the JOR-DARIT-field and SOR-DARIT-field methods have been developed as well.This paper compares the four methods from the perspectives of accuracy and convergence speed,etc.
analytical solution;electromagnetic pulse;iterative method;transient analysis;transmission line modeling;waveform relaxation
U665.26;TJ91
A
10.3969/j.issn.1673-3185.2016.04.018
2015-10-15网络出版时间:2016-7-29 9:45
国家自然科学基金面上项目(51277148);国家电网公司基础性前瞻性项目(EPRI4120-14039)
郭俊(通信作者),男,1986年生,博士生。研究方向:传输线电磁脉冲响应建模方法。
E-mail:a4edward@hotmail.com
李妮,女,1982年生,硕士,工程师。研究方向:电网电磁环境,电磁兼容及标准化研究。
E-mail:lini000@163.com

