遗传粒子群优化算法在船舶动力定位控制中的应用

薛彩霞，袁伟，俞孟蕻，樊冀生

江苏科技大学电子信息学院，江苏镇江212003

遗传粒子群优化算法在船舶动力定位控制中的应用

薛彩霞，袁伟，俞孟蕻，樊冀生

江苏科技大学电子信息学院，江苏镇江212003

针对船舶动力定位系统精确定点控制的问题，结合遗传算法（GA）独特的选择交叉变异功能和粒子群优化算法（PSO）较好的记忆功能等优点，提出了遗传粒子群（GAPSO）算法，并应用到最优控制性能指标加权矩阵的权重系数选择中。通过1艘海工多用途动力定位船舶定点控制仿真实验，使船舶纵荡和横荡的位置及艏摇角都逐渐保持在期望值，且所有输出值都收敛有界，结果与传统最优控制相比，遗传粒子群算法在最优控制中更具有效性及较好的寻优性能，有益于船舶工程的应用。

船舶；动力定位系统；最优控制；遗传粒子群算法；权重系数

0　引　言

在船舶动力定位最优控制器的设计过程中，有很多加权矩阵的权重系数需要设定，权重系数对最终的输出结果有重要的影响。一般情况下，仿真实验中都是根据系统物理特性和实践经验来确定最优控制的权重系数，如仿真结果不好，再对已输出的结果进行分析，不断修改加权矩阵的每个系数，直至仿真结果理想为止。这种通过不断实验确定加权矩阵权重系数的方法，既需要对系统的特性了解透彻，又需要花费很多时间进行调试。因此，众多学者开始深入研究如何更方便地得到较准确的权重系数。黄卫忠等［1］将遗传算法（GA）应用到最优控制加权矩阵的优化中，使得闭环系统渐进稳定，从而证明了其设计的有效性。金鸿章等［2］将遗传算法应用到舰船横摇运动的模糊建模及减摇鳍控制器的优化设计中，并与传统的控制器对比，结果表明了遗传算法在复杂系统参数优化中的有效性及优越性。谢元平［3］将遗传算子结合到粒子群算法（PSO）中用于控制系统优化。基于之前的文献研究表明，遗传算法和粒子群算法的结合增加了快速获取最优权重系数的可能性。本文将提出遗传粒子群LQG最优控制，将其应用到LQG加权系数寻优中，并通过对某海工多用途动力定位船舶的仿真，验证该方法的有效性。

1　船舶动力定位系统数学模型

在船舶动力定位系统的研究过程中，一般只考虑水平面三自由度运动［4-5］，即纵荡、横荡和艏摇。建模常用2种坐标系：大地坐标系和随船坐标系，2种坐标系之间的转换关系和低频运动模型如下：

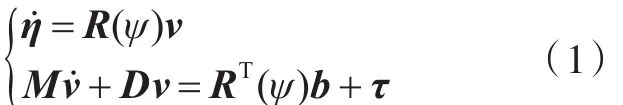
式中：向量η=［N,E,ψ］Τ为船舶在大地坐标系下纵荡、横荡位置及艏摇角；向量v=［u,υ,r］Τ为船舶在随船坐标系下纵荡、横荡速度及艏摇角速度；ψ为艏摇角；τ为船舶在纵向、横向的推进力及艏向力矩。M为系统惯性矩阵（包含附加质量）；D为阻尼系数矩阵；b表示风、浪、流的环境扰动力和力矩；R（ψ）为2种坐标系之间的转换矩阵，R（ψ）对所有的ψ都是非奇异且满足R-1（ψ）=RΤ（ψ）。

2　LQG最优控制器设计

将上述船舶的低频运动模型转换成船舶运动的状态方程

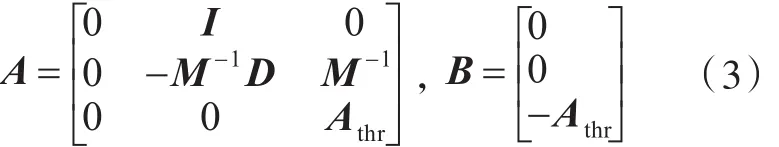
LQG控制系统如图1所示，由于系统中没有积分环节，为保证在纵荡、横荡、艏摇3个方向的状态估计值和期望值之间的误差变量最小，要在控制器中加入积分器［6］，定义一个新的状态变量：

式中，C=［I3×303×303×3］。

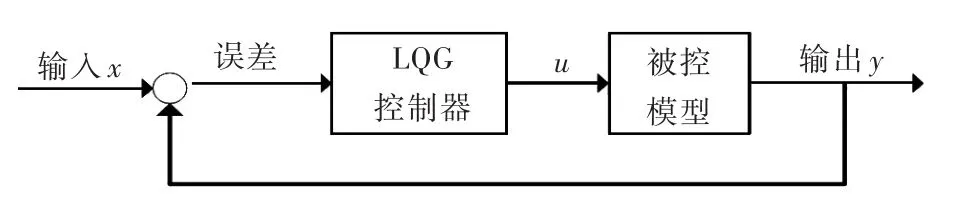
图1　LQG控制原理图Fig.1　Principle diagram of LQG control

因此，加入积分环节之后的状态方程为

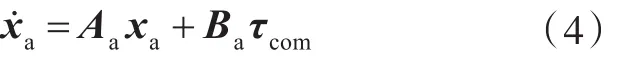
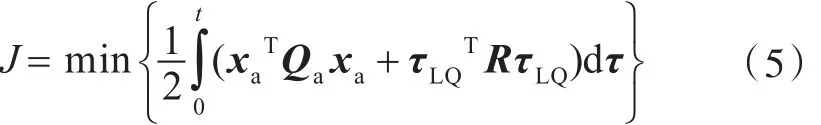
式中：xa=［zΤ,xΤ］Τ，式中：τLQ是为了达到最优性能指标，提供给推进器的3个自由度上的力和力矩；对于线性时不变系统，可由LQ控制律得到最优控制律τLQ=Gaxa=-R-1BaΤP∞x，P∞是黎卡提方程P∞Aa+AaΤP∞-P∞BaR-1BaΤP∞+Qa=0的解；Qa=diag（QIQ）≥0是半正定加权矩阵，QI=QIΤ＞0与3个自由度上的积分时间有关，Q=diag（q1q2q3）和R=diag（r1r2r3）均为

LQ控制律是通过使得J的性能指标最小化而得到，即正定加权矩阵，两者的权重系数大小决定系统对不同性能指标的重视程度，直接影响到控制器设计质量的好坏，对最优解有极大的影响，因此，其取值是本课题研究的重点。

3　遗传粒子群算法

遗传算法［7］和粒子群算法［8-9］都是模拟自然界生物活动的随机算法。但两种算法都存在优缺点，例如：遗传算法具有自组织、自适应和自学习性，其本质的并行性使其搜索全面、全局寻优能力很强，但是遗传算法的局部搜索能力差，此外编程要通过二进制码来实现，不利于实际应用，并且在迭代过程中种群发生变化时，会丧失以前的信息。相比遗传算法，粒子群算法具有记忆能力，能够保留局部个体和全部种群的最优信息，局部寻优能力较强，收敛速度快，能提高运行速度。因此，本文将结合遗传算法和粒子群算法的优点，在粒子群优化算法的基础上，通过借鉴遗传算法中的选择、交叉、变异操作的思想，实现种群多样性，形成一种新的算法——遗传粒子群算法（GAPSO），并将该算法应用到船舶动力定位LQG最优控制的性能指标加权矩阵系数的优化中，以得到最优的权重系数。

PSO描述了1个有m个粒子的种群，以一定的速度在D维空间搜索，每个粒子都在经过的最优位置以及所有粒子都经过的最优位置上进行搜索［10］。

粒子位置和速度更新公式为

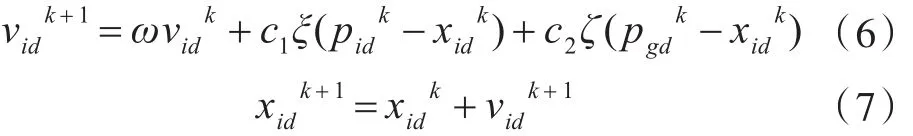
式中：xi=（xi1,xi2,...,xiD）和 νi=（νi1,νi2,...,νiD）分别是粒子在D维搜索空间的位置变量和速度变量；pid=（pi1,pi2,...,piD）和 pgd=（pg1,pg2,...,pgD）分别是个体粒子经过的最优位置以及所有粒子经过的最优位置；c1，c2是学习因子；ω是惯性权重；ξ，ζ是均匀分布在（0～1）区间内的随机数。

GAPSO优化算法具体操作方法如下：

1）设定优化参数（种群规模和选择、交叉、变异算子以及惯性权重、迭代次数、学习因子等）。

2）初始化种群的初始位置和速度，并计算适应度值。

3）将粒子当前位置作为每个粒子的个体最优值 pid，最好的作为全局最优值 pgd。

4）根据种群个体历史最优位置和种群当前最优位置，更新个体速度和位置，生成新种群。

5）计算粒子更新后的适应度值，根据适应度值排序。

6）将选择、交叉、变异算子应用到粒子群。

7）评估每个粒子的适应度值并排序。

8）寻找粒子群的个体最优 pid和 pgd。

9）如果结果满足迭代停止条件，得到最优解，否则转回步骤4），继续寻优，直至满足迭代停止条件为止。

4　仿真对比分析

控制器中的加权矩阵Q和R系数均需按图1原理进行寻优，其优化原理如图2所示，寻优目的是让输入响应的控制偏差接近零，且响应偏差较小，响应速度较快。

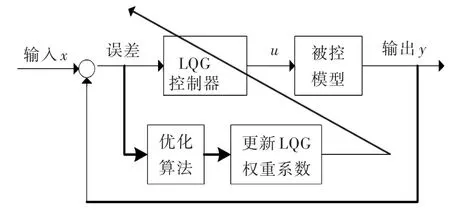
图2　LQG权重系数优化原理图Fig.2　Principle diagram of LQG weighting coefficientoptimization

其中，适应度函数选取的是误差绝对值时间积分的性能指标，为取得较好的动态特性，改进后的目标函数为，其中e为状态估计值和期望值间的误差值。

现以某海工多用途动力定位船为仿真对象，利用Matlab软件［11］来验证遗传粒子群LQG控制（GAPSO-LQG）在船舶动力定位系统中的性能，该船舶相关参数和仿真优化参数如表1所示。

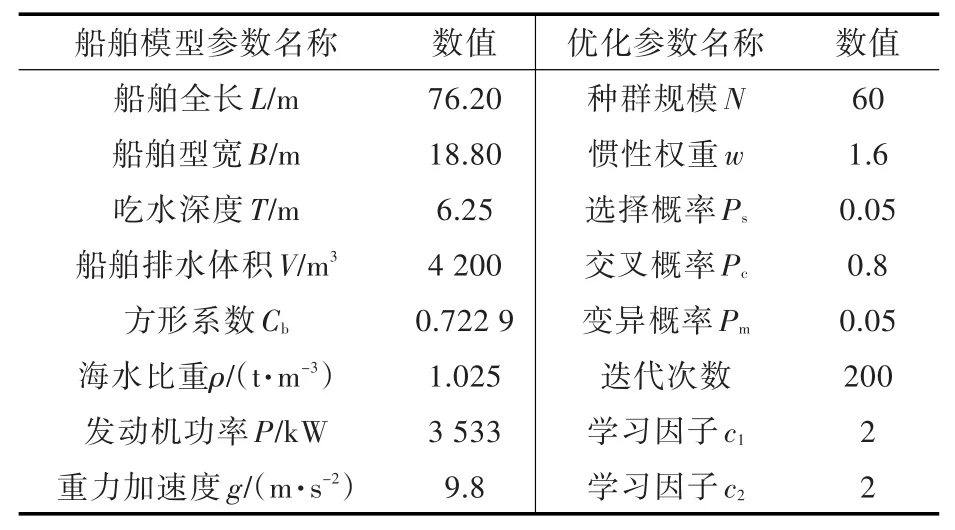
表1　仿真实验的主要参数Tab.1　The main parameters of the simulation experiment

仿真实验中，设船舶的起始位置为η（0）=［0 m0 m0°］Τ，期望位置为ηd=［50m50 m0°］Τ。由传统的不断实验方法得到LQG加权矩阵为Qa=diag（105 10），R=diag（15 1）；由遗传粒子群算法寻优得到的加权矩阵为Qa=diag（255 25），R=diag（0.25 2.5 0.25）。实验中对船舶的一些仿真结果进行了约束，如表2所示。

图3～图7给出了该实验的仿真结果，图中采用了真实值、LQG控制值以及GAPSO-LQG控制值进行对比分析。其中：真实值是指根据船舶动力定位系统的数学模型，由系统的状态方程计算得出的数值；LQG控制值是指动力定位系统中控制器应用的是LQG控制器，通过其进行定点控制，最后输出的控制值；GAPSO-LQG控制值是指动力定位系统的控制器依旧是LQG控制器，利用了GAPSO算法对LQG控制器的加权矩阵系数进行了寻优，再通过定点控制，最后输出的控制值。接下来将对每幅图进行详细分析。

表2　船舶3个方向的约束/限制Tab.2　Restrictions of the ship in three directions

图3所示为船舶在纵荡、横荡、艏摇3个自由度的位置输出真实值、LQG控制输出值以及GAPSO-LQG控制输出值，它们都明显能够达到定点的效果，最后都稳定在期望值附近。图3（a）中，GAPSO-LQG控制曲线提前进入稳定状态且超调明显小于LQG控制曲线；图3（b）中，GAPSO-LQG控制曲线提前进入稳定状态，且曲线相对平滑；图3（c）中，LQG控制的曲线和GAPSO-LQG控制曲线一开始都受到随机函数的影响，产生了一些波动，但是LQG控制的曲线明显地远离期望值，在180 s时开始接近期望值，GAPSO-LQG控制曲线一开始是在期望值附近波动，随后在不到100 s的时候就达到了期望值，并逐渐稳定且平滑。

图4所示为船舶的运动轨迹，分别为真实值的运动轨迹、LQG控制的运动轨迹以及GAPSOLQG控制的运动轨迹。LQG控制的运动轨迹最终实现了定点控制，但是控制达到稳定的时间较久，偏离期望值较远；GAPSO-LQG控制的运动轨迹一开始有一点小的波动，随后很快与真实轨迹吻合一直到期望值（50 m，50 m），表明该方法能很快平稳地达到预期的效果。

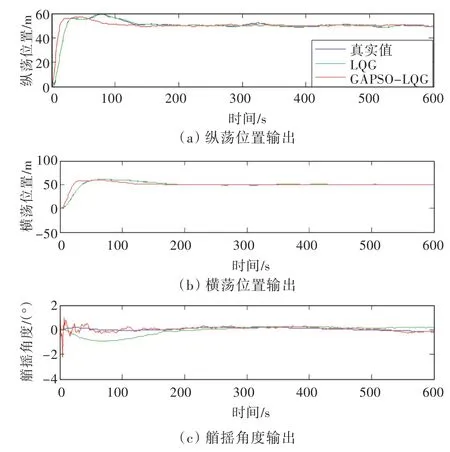
图3　船舶实际位置输出Fig.3　Ship actual position outputs

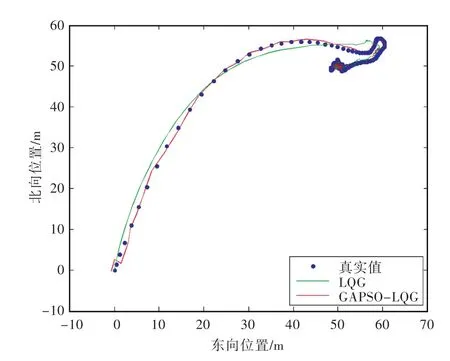
图4　起始点为（0，0）的船舶运动轨迹Fig.4　Ship motion trajectory of original position（0，0）

图5分别是船舶在纵荡和横荡方向的控制力曲线，以及船舶在艏摇方向的控制力矩曲线。图5（a）中，GAPSO-LQG控制曲线比LQG控制曲线超调小，波动幅值小并很快达到稳定；图5（b）中，GAPSO-LQG控制相对于LQG控制曲线波动性小很多；图5（c）中，GAPSO-LQG控制曲线波动幅值小，很快达到稳态，LQG控制的曲线波动幅度大，在开始段抖动厉害，达到稳态时间长。

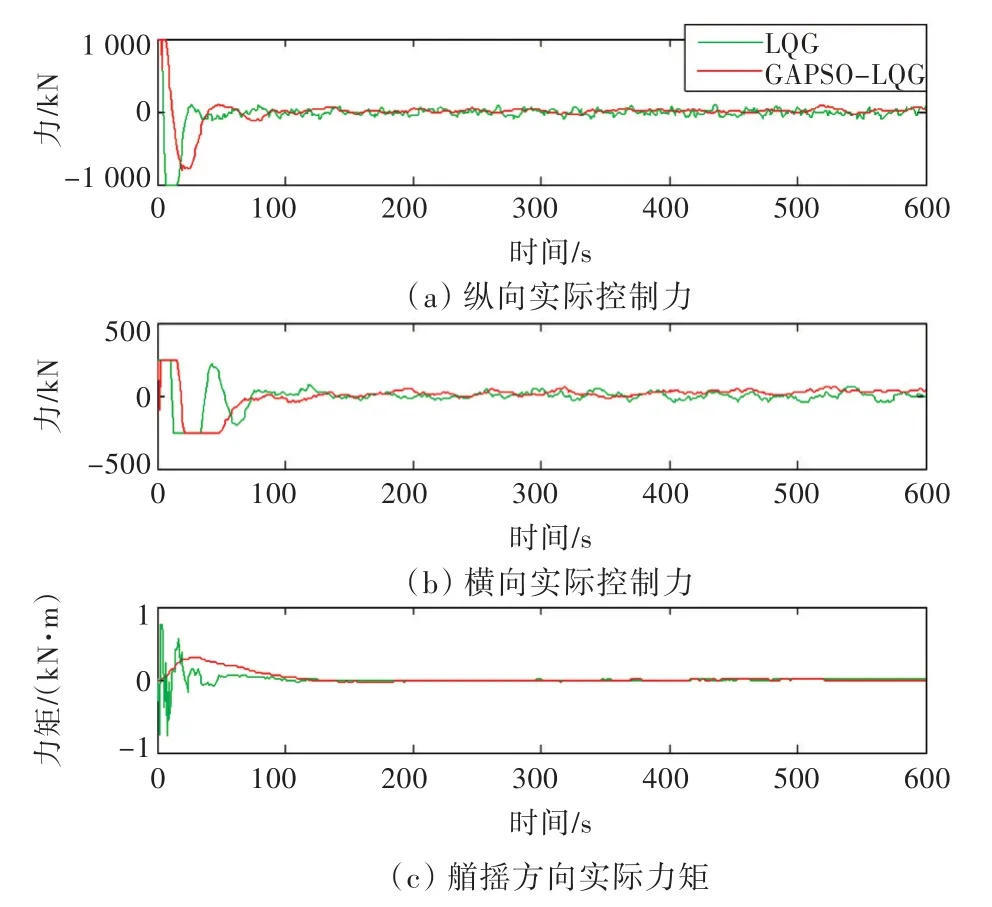
图5　控制力和力矩Fig.5　Control force and torque

图6分别是船舶在纵荡、横荡、艏摇3个方向位置输出真实值与两种算法下实际输出的误差对比。3幅图很明显地反映出GAPSO-LQG控制下的误差均值较小，船舶能够很快地精确定位且保持稳定。

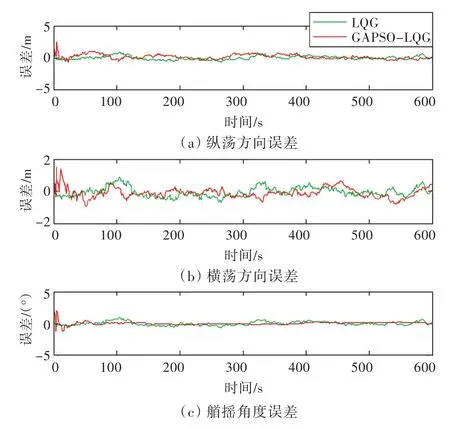
图6　船舶实际位置输出误差Fig.6　Ship actual position errors

若船舶起始位置不在原点处，将起始位置改为η（0）=［10m10 m5°］Τ，期望位置不变，仿真结果见图7。

由图7可以看出，GAPSO-LQG控制的运动轨迹能够很快、很稳定地达到期望值，实现精确定点控制，说明GAPSO算法在该系统中具有普遍性，无论船舶处于怎样的初始位置，船舶都能平稳快速地运动到设定的期望值。

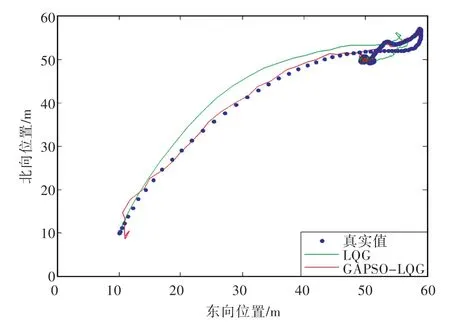
图7　起始点为（10，10）的船舶运动轨迹Fig.7　Ship motion trajectory of original position（10，10）

因此，由图3～图7可以看出：将遗传粒子群算法得出的最优加权矩阵应用到LQG控制中，使得船舶能够更快地达到平稳状态以及设定的期望值，且相对于LQG控制的结果，加入算法的曲线波动幅度较小，超调较小，能达到满意的效果，同时船舶系统的稳定性和鲁棒性增强，对船舶动力定位的定点控制仿真大有裨益。

5　结　语

本文针对传统LQG控制选择加权矩阵方法不足的问题，融合了遗传算法与粒子群算法的优点，提出了遗传粒子群算法，并应用到船舶动力定位系统LQG控制的加权矩阵选择中。通过定点控制仿真实验，船舶的纵荡位置、横荡位置、艏摇角从起始点开始运动能够逐渐保持在给定的期望值上，且动力定位系统的响应速度快、实时性增强、波动性小、稳定性和鲁棒性强，充分证明了该算法的有效性。实验结果表明：本文提出的遗传粒子群最优控制能够较好地应用到船舶动力定位系统的定点控制中，使其控制效果与其最优解更为接近。

［1］黄卫忠，高国琴.基于遗传算法的最优控制加权阵的设计［J］.计算机测量与控制，2003，11（10）：761-762，772.

HUANG Weizhong，GAO Guoqin.Design of weighting matrix for optimal controller based on genetic algorithm ［J］.Computer Measurement and Control，2003，11 （10）：761-762，772.

［2］ 金鸿章，王科俊，何琳.遗传算法理论及其在船舶横摇运动控制中的应用［M］.哈尔滨：哈尔滨工程大学出版社，2006.

［3］谢元平.改进粒子群优化算法的研究及其在控制系统设计中的应用［D］.北京：北京化工大学，2011.

［4］贾欣乐，杨盐生.船舶运动数学模型［M］.大连：大连海事大学出版社，1999.

［5］边信黔，付明玉，王元慧.船舶动力定位［M］.北京：科学出版社，2011.

［6］FOSSEN T I.Marine control systems：guidance，navigation and control of ships，rigs and underwater vehicles［M］.Trondheim：Marine Cybernetics AS，2002.

［7］周明，孙树栋.遗传算法原理及应用［M］.北京：国防工业出版社，1999.

［8］刘波.粒子群优化算法及其工程应用［M］.北京：电子工业出版社，2010.

［9］潘峰，李位星，高琪，等.粒子群优化算法与多目标优化［M］.北京：北京理工大学出版社，2013.

［10］张贝克，谢元平，马昕.结合遗传算子的改进粒子群算法在控制系统设计中的应用［J］.化工自动化及仪表，2011，38（5）：521-524.

ZHANG Beike，XIE Yuanping，MA Xin.Application of modified PSO algorithm in control system design ［J］.Control and Instruments in Chemical Industry，2011，38（5）：521-524.

［11］ 刘卫国.Matlab程序设计与应用［M］.北京：高等教育出版社，2006.

网络出版地址：http://www.cnki.net/kcms/detail/42.1755.TJ.20160729.0945.034.html期刊网址：www.ship-research.com

引用格式：徐鹏，宋振国，陈汝刚，等.船舶蒸汽管网水力热力耦合计算方法［J］.中国舰船研究，2016，11（4）：116-120.

XU Peng，SONG Zhenguo，CHEN Rugang，et al.Hydraulic and thermal coupling calculation for the steam pipe network of ships［J］.Chinese Journal of Ship Research，2016，11（4）：116-120.

Application of the genetic particle swarm optimization algorithm in dynamic positioning ship control

XUE Caixia，YUAN Wei，YU Menghong，FAN Jisheng
School of Electronic and Information，Jiangsu University of Science and Technology，Zhenjiang 212003，China

Aiming at the issue of precise fixed point control of the vessel dynamic positioning system and combining the unique function of the genetic algorithm such as sound selection of cross mutant objects and good memory for the characters of the particle swarm algorithm，a genetic particle swarm optimization algorithm is proposed in this paper and applied to the weight coefficient selection of the performance index weighting matrix of the optimal control.Through a marine multipurpose ship dynamic positioning point control simulation，the position of surge and sway as well as the angle of yaw gradually reach the desired value，and all output values are seen to converge and bounded.Compared with the results obtained in the traditional optimal control，the proposed algorithm is more effective and yields better optimization performance of the genetic particle swarm in the optimal control，and is thus more suitable for marine engineering applications. Key words：ship；dynamic positioning system；optimal control；genetic particle swarm optimization algorithm；weighting coefficient

U661.3

A

10.3969/j.issn.1673-3185.2016.04.016

2015-09-24网络出版时间：2016-7-29 9:45

江苏省产学研联合创新资金资助项目（BY2013066-08）；江苏高校高技术船舶协同创新中心/江苏科技大学海洋装备研究院资助项目（HZ2015006）；江苏省科技支撑计划（工业）（BE2011149）

薛彩霞，女，1991年生，硕士生。研究方向：船舶运动控制技术。E-mail：815562116@qq.com

俞孟蕻（通信作者），男，1962年生，教授。研究方向：船舶综合控制技术。

E-mail：Ymhzj2691@163.com