一类具有非线性发生率的生态-流行病模型分析
刘宣亮,江文超
(华南理工大学数学学院,广东广州 510640)
·数学·
一类具有非线性发生率的生态-流行病模型分析
刘宣亮,江文超
(华南理工大学数学学院,广东广州510640)
对仅在捕食者中传播且具有非线性发生率的一类生态-流行病进行了研究.考虑了系统解的有界性、边界平衡点与正平衡点的存在条件及稳定性;利用分支理论与方法讨论了正平衡点的Bogdanov-Takens分支产生的条件,得到了相应的鞍结点分支曲线、Hopf分支曲线和同宿分支曲线;对正平衡点的Hopf分支,讨论了分支的方向及稳定极限环的存在性.
生态-流行病模型;非线性发生率;稳定性;分支
【引用格式】刘宣亮,江文超.一类具有非线性发生率的生态-流行病模型分析[J].北华大学学报(自然科学版),2016,17(3): 281-289.
1 引 言
近几十年来,种群动力学和传染病动力学得到了广泛的研究,作为种群生态学与传染病动力学的一种结合,考虑疾病在相互作用的种群之间传播的生态-流行病模型也引起了人们越来越多的关注[1-9].文献[2-3]对疾病仅在食饵中传播,且疾病发生率为双线性的情形进行了研究;文献[4]进一步考虑了疾病发生率为非线性的情形,研究了其丰富的动力学性质.本文研究如下疾病仅在捕食者中传播,只有易感捕食者捕食食饵,且疾病发生率为非线性的一类捕食者-食饵模型:
其中:S,I分别表示捕食者中易感者和染病者的密度;x表示食饵的密度;r表示食饵的内禀增长率;k表示食饵种群的环境容纳量;mxS为功能性反应函数;ε为转化率;d表示捕食者的死亡率;b0I2S表示疾病的非线性发生率;c表示染病者的自然死亡率.所有参数都为正常数.
2 解的有界性
(ⅰ)若X(t)≥1对任意的t≥0都成立,则当t→+∞时,(X(t),S(t),I(t))→(1,0,0);
(ⅱ)若存在一个t0≥0使得X(t0)<1成立,则当t>t0时,有X(t)<1成立;
(ⅲ)如果X(0)<1,那么对任意的t>0,有X(t)<1成立.
(ⅰ)若X(t)≥1对任意的t≥0都成立,从系统(2)中的前两个方程可以得到
于是当X(t0)<1时,对t>t0,有X(t)<1成立.
(ⅲ)当X(0)<1时,利用(ⅱ)的证明过程可知对任意的t>0,有X(t)<1成立.证毕.
引理2存在一个M>0,使得当t充分大时,系统(2)的初值位于内的任一解(X(t),S(t),I(t))满足
0≤Y(t)≤exp(-min{a2a3,a4}(t-t*))Y(t*)+M[1-exp(-min{a2a3,a4}(t-t*))],而上式右端当t→+∞时极限为M,所以系统(2)的所有从中出发的解是最终正向有界的.证毕.
3 平衡点及其稳定性
3.1边界平衡点及其稳定性
由系统(2)容易得到以下边界平衡点E0(0,0,0),E10(1,0,0),E20(a3,a0(1-a3)/a1,0).系统(2)在平衡点E0处的特征值为a0,-a2a3,-a4,因此E0为不稳定的.在平衡点E10处的特征值为-a0,a2(1-a3),-a4,当a3>1时,E10是局部渐近稳定的;当a3<1时,E10是不稳定的.当a3<1时,在内E20存在,系统(2)在E20处的特征方程为
其特征值皆为负实部,故E20是局部渐近稳定的.
定理2当a3>1时,平衡点E10在内除坐标平面X=0外是全局渐近稳定的.
证明:当a3>1时,系统(2)在内只有E0,E10两个平衡点.取0<ε<a3-1,对初值位于内且不在坐标平面X=0上的解(X(t),S(t),I(t)),由引理1知,存在T>0,当t>T时,0<X(t)<1+ε,则,于是=0.故系统(2)的极限方程为
对于极限方程的解(X(t),I(t))(注意到X(t)>0),当t→+∞时,有(X(t),I(t))→(1,0).于是由极限系统理论[1],当t→+∞时,有(X(t),S(t),I(t))→(1,0,0).故平衡点E10在内除坐标平面X=0外是全局渐近稳定的.证毕.
3.2正平衡点及其稳定性
容易得到正平衡点(X,S,I)的I坐标满足方程:
由于f(0)>0,因此方程f(I)=0必有一负根I1.当a3≥1时,方程(3)无正根,下设a3<1.记
则有
当a0<a*0时,f(Ib)>0,方程f(I)=0无正根;当a0=a*0时,f(Ib)=0,方程f(I)=0有一个正根(二重根)I0=Ib;当a0>a*0时,f(Ib)<0,方程f(I)=0有两个正根I2,I3,不妨设I2<I3,即0<I2<Ib<I3.
在ℝ3+内,当a3>1时或当a3<1,a0<a*0时,系统(2)没有正平衡点;当a3<1,a0=a*0时系统(2)有唯一的正平衡点当a3<1,a0>a*0时,系统(2)有两个正平衡点
关于M2(X2,S2,I2)的稳定性有如下结论:
定理3当a3<1,a0>a*0时,系统(2)在正平衡点M2(X2,S2,I2)处是不稳定的.
证明:系统(2)在M2(X2,S2,I2)处的特征方程为
4 正平衡点的分支
本节讨论在正平衡点处的Bogdanov-Takens分支和Hopf分支.由于计算较繁琐,计算过程中使用了数学软件Maple.
4.1Bogdanov-Takens分支
当a3<1,a0=a*0时,系统(2)有唯一的正平衡点M0(X0,S0,I0).记
在条件a0=a*0,a4=a*4下,容易得到系统(2)在正平衡点M0处有两个零特征值.下面利用文献[10]中的方法来讨论在M0附近的Bogdanov-Takens分支.
我们选取a0,a4为分支参数来研究.将系统(2)记为
其中Z=(X,S,I)T,U=(a0,a4)T.记Z0=(X0,S0,I0)T,U0=(a*0,a*4)T,则F(Z0,U0)=0,DF(Z0,U0)的特征值为0,0,-b1,其中
记矩阵
又设P-1=(q1,q2,q0),则
其中
从而利用文献[10]中的公式和记号,经计算得到
其中
最后利用文献[11]中关于Bogdanov-Takens分支的结论,可得:
(ⅰ)有鞍结点分支曲线:SN={(λ1,λ2):4aβ1-β22=0};
(ⅱ)有Hopf分支曲线:H={(λ1,λ2):β1=0,β2<0};
(ⅲ)有同宿轨分支曲线:HL={(λ1,λ2):25aβ1+6β22=o(β22),β2<0}.
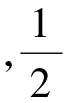
相应分支曲线为
4.2Hop f分支
当a3<1,a0>a*0时,系统(2)有两个正平衡点M2,M3,其中M2不稳定.下面讨论系统(2)在M3处的Hopf分支.
令v1=X-X3,v2=S-S3,v3=I-I3,则系统(2)可写为
其中
矩阵A1的特征方程为
其中
由于2a*0I30=a1a2a4,又a0>a*0,I3>I0,可知γ=X3S3(2a0I33-a1a2a4)>0,故方程(7)必有一个负根.如果特征方程(7)有纯虚根iω0(ω0>0),将λ=iω0代入方程(7)中,可得αβ-γ=0,即Δ≡a0a1a2X23S3+ a0a24X3-2a24I23-a20a4X23=0.设有a*1>0,当a1=a*1时,Δ=0,β>0,即当a1=a*1时,方程(7)有一对纯虚根 ±iω0,ω0=又设λ=μ(a1)+iω(a1)为方程(7)的一个复根,代入方程(7),可得
方程(9)两边对a1求导,利用μ(a*1)=0,ω(a*1)=ω0,可得
如果μ'(a*1)≠0,则产生Hopf分支的横截性条件满足.
下面讨论Hopf分支的方向.
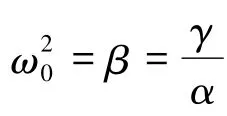
其中
通过变换z=y1+i y2,y3=u,把方程(10)变为复数形式
其中
不妨设方程(11)在原点附近的中心流形可以表示为
其中
利用一阶Lyapunov系数的计算公式[11]:
可以得到一阶Lyapunov系数l1(0).由于一般参数下l1(0)的表达式太长,不易讨论其正负,我们略去l1(0)的具体表达式,下面取一组特定参数值来讨论原系统的Hopf分支的方向.
[1]马知恩.传染病动力学的数学建模与研究[M].北京:科学出版社,2004.
[2]Chattopadhyay J,Arino O.A predator-preymodelwith disease in the prey[J].Nonlinear Analysis,1999,36(6):747-766.
[3]Xiao Y,Chen L.Analysis of a three species eco-epidemiologicalmodel[J].Journal of Mathematical Analysis and Applications,2001,258(2):733-754.
[4] Liu X L.Bifurcation of an eco-epidemiological model with a nonlinear incidence rate[J].Applied Mathematics and Computation,2011,218(5):2300-2309.
[5]幸玲,刘宣亮.具饱和传染率的一类捕食者-食饵模型的分析[J].南京师大学报(自然科学版),2011,34(3):25-31.
[6]Sasmal K M,Chattopadhyay J.An eco-epidemiological system with infected prey and predator subject to theweak Allee effect[J]. Mathematical Biosciences,2013,246(2):260-271.
[7]Bate A M,Hilker FM.Complex dynamics in an eco-epidemiologicalmodel[J].Bull Math Biol,2013,75(11):2059-2078.
[8]王淑璠,马智慧,李文龙,等.具有庇护所效应的生态流行病模型[J].兰州大学学报(自然科学版),2013,49(5): 703-708.
[9]童姗姗,连冬艳,马戈.一类含有避难所和收获的生态流行病模型的稳定性[J].北华大学学报(自然科学版),2016,17(1):15-19.
[10]Carrillo F,Verduzco F.Analysis of the Takens-Bogdanov bifurcation on m-parameterized vector fields[J].International Journal of Bifurcation and Chaos,2010,20(4):995-1005.
[11]Kuznetsov Y.Elements of applied bifurcation theory[M].New York:Springer,1998.
【责任编辑:伍林】
Analysis of an Eco-Epidemiological Model with a Nonlinear Incidence Rate
Liu Xuanliang,Jiang Wenchao
( School of Mathematical Sciences,South China University of Technology,Guangzhou 510640,China)
An eco-epidemiological model with a nonlinear incidence rate in the predator is considered.We analyze the boundedness of solutions and stability of equilibria.By using bifurcation methods and techniques,we study the Bogdanov-Takens bifurcation near a positive equilibrium,and obtain a saddle-node bifurcation curve,a Hopf bifurcation curve and a homoclinic bifurcation curve. The direction of Hopf bifurcation and the existence of a stable limit cycle near a positive equilibrium are also discussed.
eco-epidemiological model; nonlinear incidence rate; stability; bifurcation
O175.14
A
1009-4822(2016)03-0281-09
10.11713/j.issn.1009-4822.2016.03.001
2016-02-26
国家自然科学基金项目(11572127).
刘宣亮(1965-),男,博士,副教授,主要从事动力系统及其应用研究,E-mail:liuliang@scut.edu.cn.

