数据缺失情况下具有测量误差的两个几何分布总体参数的估计和检验
赵志文,杨慧超,何静花,梁滨滨
(吉林师范大学数学学院,吉林四平 136000)
数据缺失情况下具有测量误差的两个几何分布总体参数的估计和检验
赵志文,杨慧超,何静花,梁滨滨
(吉林师范大学数学学院,吉林四平136000)
讨论了部分数据缺失且存在测量误差的两个几何分布总体参数的估计与检验问题,给出了模型参数的矩估计,证明了估计量的强相合性和渐近正态性以及检验统计量的极限分布.
几何分布;数据缺失;测量误差;矩估计
【引用格式】赵志文,杨慧超,何静花,等.数据缺失情况下具有测量误差的两个几何分布总体参数的估计和检验[J].北华大学学报(自然科学版),2016,17(3):296-300.
几何分布是十分重要的离散分布,在众多领域有着广泛的应用[1].用统计方法处理实际问题时,常会遇到数据缺失情况,譬如在产品寿命试验中,由于试验设备、观测手段或其他方面的困难造成某些试验数据的丢失或未被观测到等.因此,在数据缺失的条件下,对不完全数据进行科学、有效的处理已成为一个非常重要的研究领域[2].对于具有缺失数据几何分布总体的统计推断问题,杨振海等讨论了几何分布的参数估计及应用[3];赵志文等讨论了具有部分缺失数据的两个几何分布总体参数的估计与检验[4];刘银萍等讨论了定时截尾下具有缺失数据的两个几何总体参数的估计[5];文献[6-7]主要讨论了其他几种离散分布在缺失数据的情形下总体参数的估计问题.而在许多实际应用中,比如农业生产、抽样调查等试验,由于人为的因素或其他方面的限制,总会出现测量不准确,从而导致得到的数据存在测量误差,因此,具有测量误差数据的统计推断问题已经成为统计学家关注的另一个新问题.对于测量误差数据,文献[8-9]主要讨论了测量误差模型参数估计与检验以及平均估计等问题;文献[10]讨论了测量误差统计模型问题;文献[11]讨论了测量误差的近似回归问题.通常情况下许多人都忽略测量误差,仅仅考虑在理想状态下具有缺失数据的分布函数总体的估计问题与检验问题.但是如果忽略测量误差,往往会导致估计是有偏差的甚至是不相合的.本文主要研究了在数据缺失的情况下具有测量误差的几何分布总体参数估计问题及假设检验问题,给出了模型参数的矩估计,参照传统测量误差模型的方法,证明了估计量的强相合性和渐近正态性以及检验两总体参数相等的检验统计量的极限分布,同时通过随机模拟对其进行验证.
1 矩估计及其渐近性质
设有两个几何分布,其密度函数为
其中0<θ<1是未知参数,分别对两个几何分布总体进行n次独立观测,在对每个总体抽取样本进行观测时,每个样本观测值以概率1-p被丢失并且存在测量误差.第一个总体观测值为(Xi,δi)(i=1,2,…,n),其中Xi表示来自第一个几何分布总体的第i个样本值,并且带有测量误差,即Xi=Yi+εi(i=1,2,…,n),其中Yi表示第i个样本真值,不能被观测到,εi表示第i个样本的观测误差,服从均值为0、方差为1的分布,并且Yi与εi相互独立.此外,如果第i个样本丢失,记δi=0,否则记δi=1.第二个总体观测值为(Zi,ηi)(i=1,2,…,n),其中Zi表示来自第二个几何分布总体的第i个样本值,并且带有测量误差,即Zi=Vi+ φi(i=1,2,…,n),其中Vi表示第i个样本真值,不能被观测到,φi表示第i个样本的观测误差,服从均值为0、方差为1的分布,并且Vi与φi相互独立.如果第i个样本丢失,记ηi=0,否则记ηi=1.
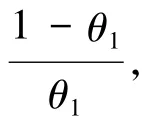
同理,在得到一组观测值(Zi,ηi)后,可得θ2的矩估计
对于上述θ1的矩估计,我们有下面的相合性和渐近正态性:
证明:由于{δiYi,1≤i≤n}为n个独立同分布的随机变量,由强大数定律知
同理可得
因此
下面我们证明估计量的渐近正态性.
定理2在前述记号下,有
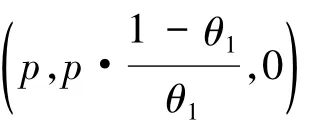
记
其中
令
则有
由引理1知
其中
即
同理可证
证毕.
2 两个总体参数相等的检验及两个总体参数之差的渐近置信区间
在实际问题中,我们常常关心两组样本是否来自同一总体,这一问题可以归结为检验两个总体参数相等的问题.为了达到这一目的,我们考虑假设检验:
特别地,在原假设H0下,我们有
令Δθ=θ1-θ2.下面考虑Δθ的置信区间.

因此,对于给定的置信水平α,Δθ的置信区间为
3 随机模拟
下面通过随机模拟说明本方法的优劣.表1给出的是样本容量n=100,置信水平α=0.95,缺失概率1 -p=0.10时的模拟结果,其中表示参数差的绝对值,以及分别表示参数θ1以及参数θ2的估计的偏差及置信区间的覆盖率(C.P.).表1给出以及的值为随机模拟1 000次的平均值,覆盖率为随机模拟1 000次的覆盖率.
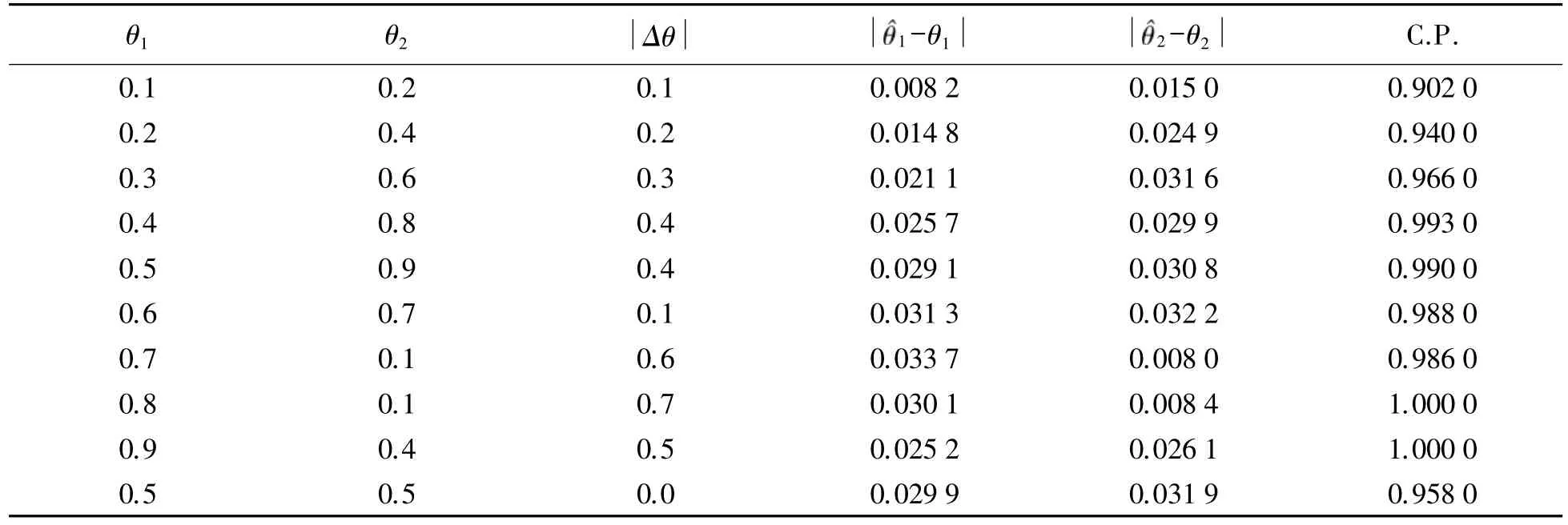
表1 模拟结果Tab.1 Simulation results
从表1的模拟可以看出,无论是较小的样本量还是较大的样本量,本文的估计方法都有较小的误差,并且误差相对稳定,的置信区间覆盖率非常高,说明本文的方法具有较高的精度.
[1]朱五英.具有部分缺失数据两个几何分布总体的估计[J].安徽师范大学学报(自然科学版),2008,31(1):13-15.
[2]刘菡.定数截尾缺失数据下双参数指数分布的统计推断[D].武汉:华中科技大学,2006.
[3]杨振海,王松桂.几何分布的参数估计及应用[J].应用概率统计,1998,14(1):31-37.
[4]赵志文,宋立新,刘银萍.具有部分缺失数据的两个几何分布总体参数的估计与检验[J].统计与决策,2010,26(5): 22-23.
[5]刘银萍,高敏,王艳.定时截尾情形具有部分缺失数据两个几何总体参数的估计与检验[J].吉林师范大学学报(自然科学版),2013,34(3):10-14.
[6]孟俊才,贺瑞缠.样本数据缺失情形下泊松过程的强度估计和检验[J].价值工程,2011,30(32):297-298.
[7]谭旭.具有部分缺失数据时两个二项总体的极大似然估计与贝叶斯估计[D].昆明:云南大学,2012.
[8]张娟.若干测量误差模型的估计与检验[M].北京:北京师范大学,2009.
[9]王海鹰,邹国华.线性测量误差模型的平均估计[J].系统科学与数学,2012,32(1):1-14.
[10]FullerW A.Measurement errormodels[J].Review of Economic Studies,2005,73(4):1201-1210.
[11] Keller ASWJB.Approximations for regression with covariate measurement error[J].Journal of the American Statistical Association,2012,83(404):1057-1066.
【责任编辑:伍林】
Parameter Estimation and Hypothesis Testing of Two Geometric Distribution Populations with Measurement Error and Missing Data
Zhao Zhiwen,Yang Huichao,He Jinghua,Liang Binbin
( College of Mathematics,Jilin Normal University,Siping 136000,China)
The paper discussed parameter estimation and hypothesis testing of two geometric distribution populations with measurement error and missing date.Moment estimation of the model parameters is given,which proves the estimator of the strong consistency and asymptotic normality and limiting distribution of the test statistics.
geometric distribution; missing data; measurement error; moment estimation
O212.1
A
1009-4822(2016)03-0296-05
10.11713/j.issn.1009-4822.2016.03.003
2016-01-21
吉林省科技发展计划项目(201201082).
赵志文(1976-),男,博士,副教授,硕士生导师,主要从事时间序列分析研究,E-mail:zhaozhiwen@126.com.

