非线性机械系统动力分析的辛时间子域-迭代法

李纬华，牛喜山

(1.广东技术师范学院机电学院，广东广州　510635；2.广东华方工程设计有限公司，广东广州　510220)



非线性机械系统动力分析的辛时间子域-迭代法

李纬华1，牛喜山2

(1.广东技术师范学院机电学院，广东广州510635；2.广东华方工程设计有限公司，广东广州510220)

建立了用于非线性机械动力响应分析的辛时间子域-迭代法.首先，在任一时间子域内，将原非线性动力方程分解为线性和非线性两部分.对于线性方程，采用基于相空间非传统Hamilton型变分原理的辛时间子域法求解.将线性响应代入非线性项并视其为载荷，重复使用辛时间子域法迭代求解至一定精度，各解叠加即得原方程在当前时间子域的数值解.然后，将这个时间子域的末端值作为下个时间子域的初始值，进行下一个时间子域的计算，如此递推下去直到最后一个时间子域.结果表明，该方法具有较高的计算精度和计算效率.

非线性动力学；辛时间子域法；迭代法；变分原理；机械系统

非线性动力学的基础理论是机械工程、土木工程、航空航天等工程学科的重要基础.机械工程中存在诸多的非线性问题，机械系统中零部件的间隙、摩擦，非线性元件的存在和构件具有的粘弹性质，都会影响系统的动力学行为，继而影响工作性能和可靠性[1].

对于多自由度非线性动力学模型，可采用解析法和数值法求解.虽然解析法在不断发展，但目前只能求解一些特殊的问题.因此，为满足实际工程需要还需研究高性能的数值方法.对非线性动力问题，常用的数值方法可分为两大类.一类是直接积分法，如Newmark法、Wilson法、Houbolt法等，这类方法简便易用，但存在能量耗散与相位误差.另一类是将二阶常微分方程组降为一阶常微分方程组，再用数值方法求解，如Runge-Kutta法、Adams多步法、Taylor法和精细积分法[2]等.对于线性动力问题，基于Hamilton对偶方程的精细积分法几乎可得到计算机上的精确解，将其用于非线性动力问题时，也取得了一定的进展.文献[3]利用同伦变换将非线性方程组转化为线性常微分方程组，然后利用精细积分法求解.文献[4]将非线性方程组转化为线性变系数常微分方程，利用高阶乘法摄动法确定传递矩阵，然后再用精细积分法求解.文献[5-8]将非线性项纳入非齐次项，对非齐次项采用钟-林格式、增维齐次化方法和直接数值积分方法处理并求解，这几种处理方法或需要矩阵求逆，或大幅增加计算量，或忽视了矩阵指数函数的性质.

动力学变分原理构造算法，简便易行且具有很好的通用性和较高的计算效率.文献[9-12]基于离散的变分原理构造了一系列能够保辛和动量或保辛且保能量和动量的算法.高强等[13]通过修正作用量给出了动力学初值问题的一系列保辛算法;罗恩等[14]基于相空间非传统Hamilton变分原理提出了求解线性动力方程的辛时间子域法.其中，辛时间子域法是一种无条件稳定的算法，其计算精度与精细积分法相当，但在非线性动力系统的应用研究还不够深入.本文在此基础上，将辛时间子域法与迭代法相结合，建立求解非线性机械系统动力响应的辛时间子域-迭代法.算例结果表明，该方法具有较高的计算精度和计算效率.

1　线性动力体系的辛时间子域法

一般地，集中质量模型的多自由度非线性动力学方程可表示为

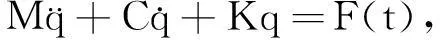
(1)

对(1)式所表示的线性动力方程，当初始条件满足时，其相空间非传统Hamilton变分原理的泛函可表示为

(2)

其中,p=Mq为动量列阵;p1和q1分别为时间末端点的动量和位移列阵;∘表示限制变分;～表示初始值.

对任一时间子域[ti,ti+1]，用m次Lagrange插值多项式近似待求的位移与动量，即

(3)

其中

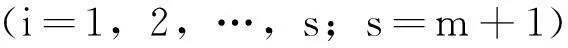
其中，a和b分别是待定的时间子域插值点的位移和动量列阵;φi(t)为Lagrange插值多项式的表达形式.此处插值点为高斯积分点.

将(3)式代入(2)式，取t1=Δt=ti+1-ti，采用具有m个积分点的高斯积分法积分，可得

(4)

(5)

其中，

从(5)式可以得到

(6)

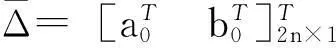
(6)式为辛时间子域法的计算递推格式.计算出各系数矩阵后，求解线性方程组(6)式即可得到当前时间子域内各时间点的位移和动量.将该时间子域末端的结点位移和动量向量作为下一时间子域的初始状态值，继续计算下去就形成递推.

2　非线性动力体系的辛时间子域-迭代法

集中质量模型的多自由度非线性动力学方程可表示为

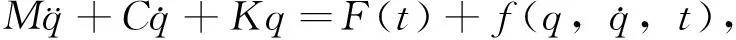
(7)

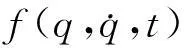
记(7)式的解为q(t)，对弱非线性问题，可设

(8)

其中q0(t)是对应线性方程(1)的解.

将(8)式代入(7)式

(9)

原非线性动力方程可以分离为线性和非线性两部分，即

(10)

(11)

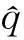
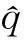
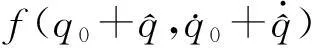
(12)

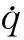
(13)

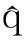
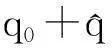
(14)

将(10)～(11)式的解叠加，即得到原非线性动力方程在当前时间子域的解.将这个时间子域的末端值作为下一时间子域的初始值，进行下一个时间子域的计算，如此递推下去直到最后一个时间子域，这就是本文建立的辛时间子域-迭代法.

3　数值仿真

3.1非线性单摆

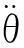
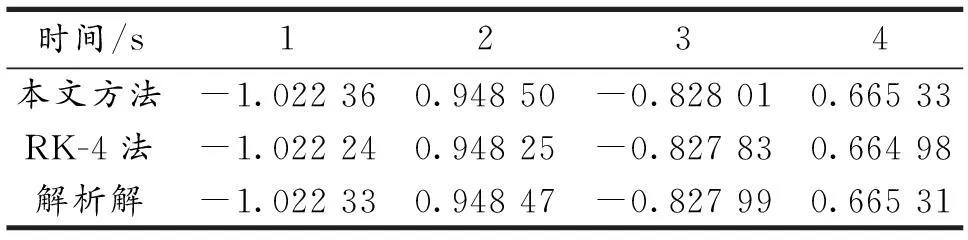
表1　非线性单摆幅角计算结果比较(rad)

3.2非线性转子系统

对非平衡的Jeffcott转子，如图1所示.该转子系统为轴对称系统，故只考虑其在一个平面内的振动.设盘的位移为x，支承质量的位移为y，则转子系统的振动方程为[15]

(15)

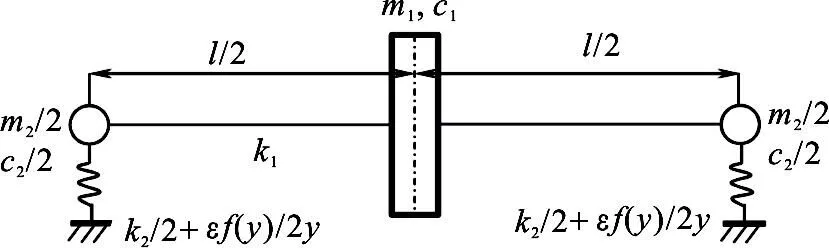
图1　非线性转子系统示意图

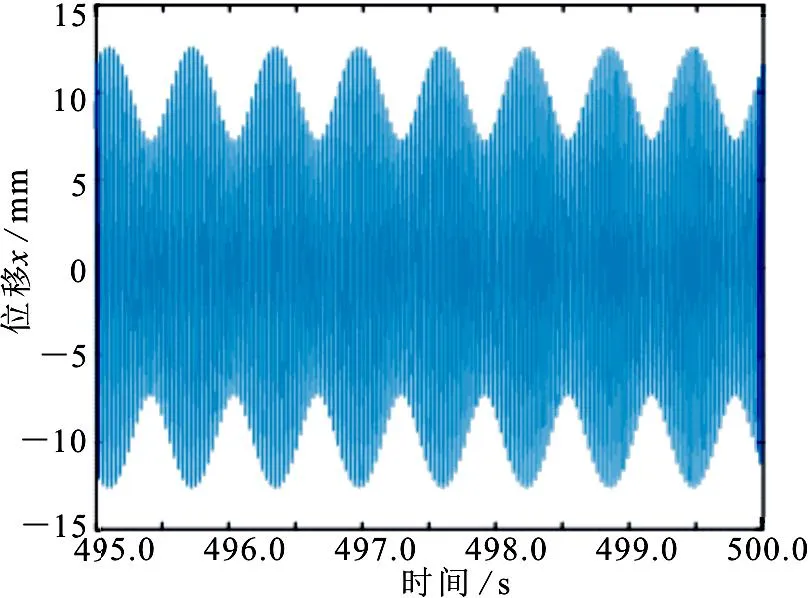
(a)x方向位移响应

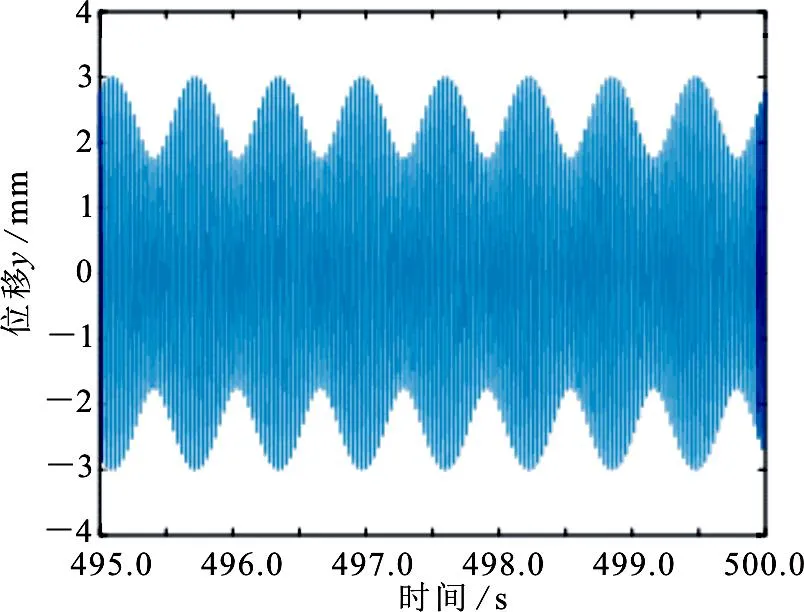
(b)y方向位移响应

时间/s200300400500本文方法(Δt=0.01s)-8.912781.958729.0601111.41802-2.142960.476012.183982.73173RK-4法(Δt=0.001s)-8.912691.958989.0605711.41793-2.143010.475832.184012.73196

两者结果吻合.说明本文方法取较大时间步长，经长时间计算(t=0～500s)后，仍可保持较高精度，是一种高性能的算法.

3.3非线性平行不对中转子系统

在旋转机械中，转子不对中是不可避免的，是引起机械故障的重要原因.对图3所示平行不对中转子系统，其无量纲化后的动力方程组为[16]

图3　不对中转子系统示意图

(16)

取ω0=0.2,ζ=0.2,ε=0.5，零初始条件，采用本文方法(m=2,Δt=0.08)计算得到系统的位移响应及轴心轨迹如图4所示(响应均是经过充分衰减后的稳态解)，可以看出此时系统的振动是准周期的；若ε=2，其他参数不变，从图5所示的结果可以看出，此时的振动具有周期性，这与实际情况比较相符.

(a)x方向位移响应图

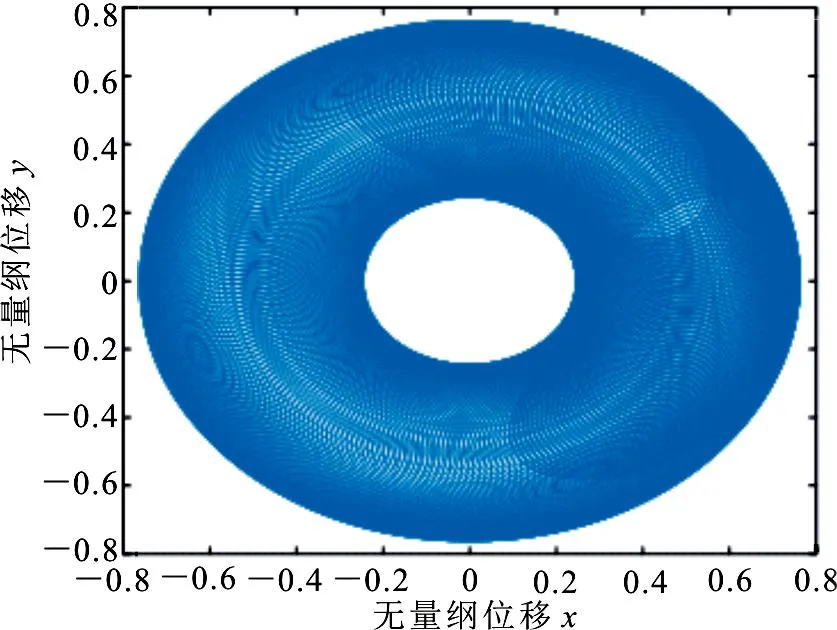
(b)轴心轨迹图

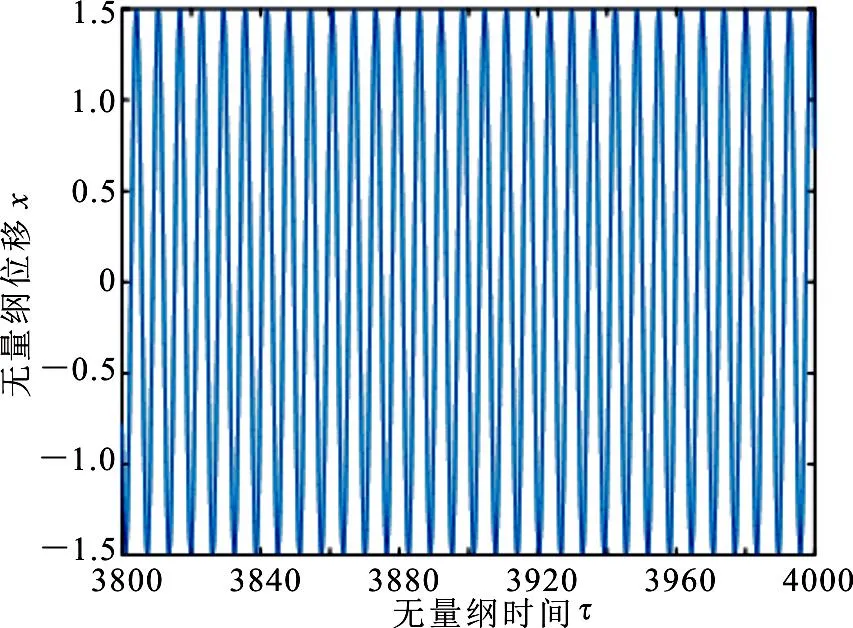
(a)x方向位移响应图

(b)轴心轨迹图

4　结论

将非线性机械系统的动力方程从形式上分离为线性和非线性两部分，结合哈密顿系统的辛时间子域法和迭代法，建立了计算系统动力响应的辛时间子域-迭代法.该法继承和发展了辛时间子域法，也补充和丰富了非线性机械系统动力响应的分析方法.通过对非线性单摆、转子系统和不对中转子系统的动力响应计算，可以看出该法具有较高的计算精度和计算效率，是求解非线性机械系统动力问题的一种有效方法.

[1]李华，沈允文，徐国华，等.机械非线性动力学分析的A-算符方法[J].机械工程学报，2002,38(7)：31.

[2]ZHONGWX，WILLIAMSFW.Aprecisetimestepintegrationmethod[J].Journal of Mechanical Engineering Science，1994，208：427.

[3]梅树立，张森文.基于精细积分技术的非线性动力学方程的同伦摄动法[J].计算力学学报，2005，22(6)：665.

[4]富明慧，蓝林华，陆克浪，等.时变动力系统的高阶乘法摄动方法[J].中国科学：G辑，2012，42(2)：185.

[5]林家浩，沈为平，宋华茂.结构非平稳随机响应的混合型精细积分[J].振动工程学报，1998，8(2)：127.

[6]顾元宪，陈飚松，张洪武.结构动力方程的增维精细积分方法[J].力学学报，2000，32(4)：447.

[7]向宇，黄玉盈，黄坚强.一种新型齐次扩容精细积分法[J].华中科技大学学报(自然科学版)，2002，30(11)：74.

[8]张森文，曹开彬.计算结构动力响应的状态方程直接积分法[J].计算力学学报，2000，17(1)：94.

[9]WENDLANDTJM，MARSDENJE.Mechanicalintegratorsderivedfromadiscretevariationalprinciple[J].PhysicaD:Nonlinear Phenomena，1997，106(3-4)：223.

[10]KANC，MARSDENJE，ORTIZM.Symplectic-energy-momentumpreservingvariationalintegrators[J].Journal of mathematical physics，1999，40(7)：3353.

[11]GONZALEZM，SCHMIDTB，ORTIZM.Energy-steppingintegratorsinlagrangianmechanics[J].International Journal for Numerical Methods in Engineering，2010，82(2)：205.

[12]LEOKM，ZHANGJ.DiscreteHamiltonianvariationalintegrators[J].IMAJournal of Numerical Analysis，2011，31(4)：1497.

[13]高强，彭海军，张洪武，等.基于哈密顿动力系统新变分原理的保辛算法之三：数值算例[J].计算力学学报，2013，30(4)：474.

[14]LUOE，HUANGWJ，ZHANGHX.UnconventionalHamilton-typevariationalprincipleinphasespaceandsymplecticalgorithm[J].Science in China:SeriesG，2003，46(3)：248.

[15]赵又群，柴山，曲庆文，等.非线性转子系统动态特性分析的模态-摄动方法[J].机械工程学报，2002，38(1)：39.

[16]李明.平行不对中转子系统的非线性动力学行为[J].机械强度，2005，27(5)：580.

(责任编辑孙对兄)

Symplectic time subdomain iterative method formechanicalsystemswithnonlinearities

LIWei-hua1,NIUXi-shan2

(1.College of Electromechanical Engineering,Guangdong Polytechnic Normal University,Guangzhou 510635,Guangdong,China;2.GuangdongHuafangArchitectural&EngineeringDesignCo.,LTD,Guangzhou510220,Guangdong,China)

Asymplectictime-subdomainiterativemethodfornonlinearmechanicalsystemisproposedinthispaper.Firstly,theresponseofthenonlineardynamicequationisdividedintothelinearpartandnonlinearpartinanytime-subdomain.Forthelinearpart,symplectictime-subdomainalgorithmbasedonunconventionalHamiltonincrementalvariationalprincipleinphasespace,isusedtosolvethelinearequation.Thenonlineartermistreatedasloadbysubstitutingwiththelinearresponse,thusthesymplectictime-subdomainalgorithmisusedrepeatedlyuntiltheerrorissatisfied.Thesolutionsoftwopartscanbecomposedtogethertogetthenumericalresultsoforiginalequationincurrenttime-subdomain.Then,theobtainedendvaluesarealsoregardedastheinitialvaluesofthenexttimesubdomainandtheiterationwillberepeateduntilthevaluesofthefinaltimesubdomain.Numericalexampleispresentedtodemonstratetheaccuracyandthecomputationalefficiency.

nonlineardynamics;symplectictimesubdomainalgorithm;iterativemethod;variationalprinciple;mechanicalsystems

10.16783/j.cnki.nwnuz.2016.04.006

2016-03-10;修改稿收到日期:2016-05-03

国家自然科学基金资助项目(11202247)

李纬华(1978—)，女，甘肃庆阳人，讲师，博士.主要研究方向为哈密顿体系下工程结构动力分析的理论和方法.E-mail:lwh927@163.com

O313.2

A

1001-988Ⅹ(2016)04-0022-05