新型缩减矩阵构造加快特征基函数法迭代求解*

王仲根 沐俊文 林涵 聂文艳

1) (安徽理工大学电气与信息工程学院, 淮南 232001)

2) (淮南师范学院机械与电气工程学院, 淮南 232001)

1 引 言

矩量法[1]是求解频域积分方程的一种有效数值方法, 被广泛应用于目标雷达散射截面计算、天线设计与分析、电磁环境预估、电磁兼容设计等领域.但矩量法需要对目标精细剖分, 随着目标电尺寸的增大, 计算复杂度以及内存需求都会急剧增大.为解决这个问题, 一些快速有效的矩量法被提出来, 如快速多极子法(fast multipole method,FMM)[2]、多层快速多极子法 (multilevel fast multipole method, MLFMM)[3,4]、预修正-快速傅立叶变换法(precorrected fast Fourier transform,P-FFT)[5]、自适应积分法(adaptive integral method, AIM)[6]等, 这些方法可以降低矩阵向量积计算复杂度, 但不能减少未知数的数目.为降低未知数的数目, 有学者提出将宏基函数引入到矩量法中, 如子全域基函数法[7]、复合基函数法[8]、子域多层法[9]、特征模法[10,11]以及特征基函数法(characteristic basis function method, CBFM)[12-14],其中CBFM因考虑到各子域间的耦合作用而备受关注.为提高CBFM计算效率, 文献[15]提出应用物理光学法生成特征基函数(characteristic basis functions, CBFs), 但精确度不高; 文献[16,17]分别应用自适应交叉近似-LU分解技术、自适应交叉近似-奇异值分解来高效生成CBFs; 文献[18,19]提出一种CBFs融合构造方法, 提高了CBFM的计算精度; 文献[20-23]应用自适应交叉近似(adaptive cross approximation, ACA)算法、快速偶极子法加快矩阵向量积运算, 提高缩减矩阵构造效率; 文献[24-26]将CBFM与MLFMM, AIM,P-FFT相结合, 通过迭代法求解缩减矩阵方程, 提高了CBFM分析电大目标电磁散射问题的能力,但是随着目标电尺寸的增大, CBFs数目不断增加,缩减矩阵维数会变得越来越大, 矩阵条件数变差,迭代求解缩减矩阵方程效率降低[27].

本文提出一种新型缩减矩阵构造方法, 应用奇异值分解技术压缩激励源, 基于新激励源求解出各子域的特征基函数.运用伽略金方法构造缩减矩阵时, 将新激励源和特征基函数作为检验函数和基函数, 得到一个对角子矩阵均为单位矩阵的缩减矩阵.新方法构造的缩减矩阵与传统方法构造的缩减矩阵相比, 矩阵条件数得到了优化, 迭代求解缩减矩阵方程的效率显著提高, 并且该方法易于与MLFMM, AIM, P-FFT等算法相结合, 进一步提高了特征基函数法分析电大尺寸目标电磁散射问题的能力.

2 特征基函数法

CBFM首先将目标划分为M个邻接的子域,再将每个子域剖分成Ni个单元(i=1, 2,...,M).为获得一组包含多角度电流信息的CBFs,CBFM采用不同入射方向和极化的激励照射每个子域, 假设总的激励数为Npws=2NθNϕ,Nθ,Nϕ分别表示在θ,ϕ方向上的激励数目, 于是子域i上的主要特征基函数(primary characteristic basis functions, PCBFs)即可通过下式求得:

式中,Ei表示扩展子域i的激励矩阵, 维数为表示扩展子域i的自阻抗矩阵, 维数为为扩展子域i的电流系数矩阵,维数为为扩展子域i的未知数数目.通过直接求解(1)式, 得到扩展子域i的.由于采用多角度激励源得到的必然含有冗余信息,故通过奇异值分解(singular value decomposition,SVD)压缩矩阵去除冗余信息, 即

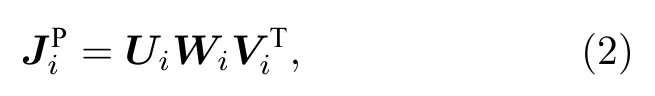
式中,Ui和Vi均为酉矩阵, 维数分别为和为对角阵, 维数为通过设置合适的门限τ, 保留Ui中大于门限的前Ki个列向量并去除扩展部分作为子域i的最终CBFs.假设子域i经过 SVD后得到Ki个 CBFs,则子域i的表面电流可由这Ki个CBFs线性组合表示:

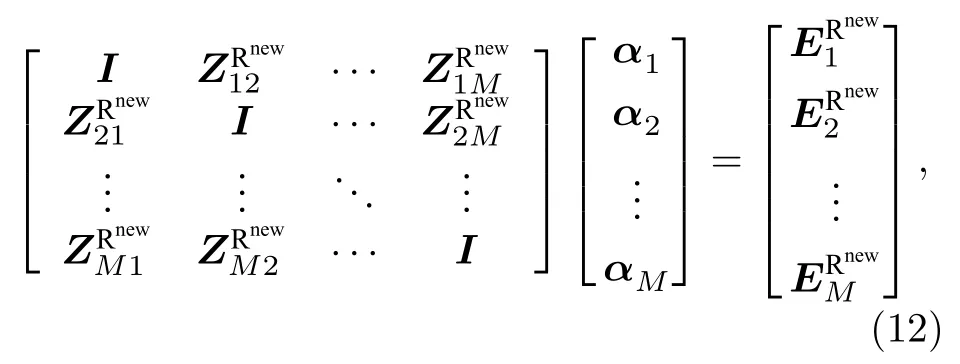
式中,ZR表示所有子域CBFs之间的相互作用,维数为是激励向量;α为待求CBFs系数.缩减矩阵方程构造原理与矩量法构造阻抗矩阵方程相似, 子域i上的第m个CBFs与子域j上第n个CBFs之间的相互作用表示为

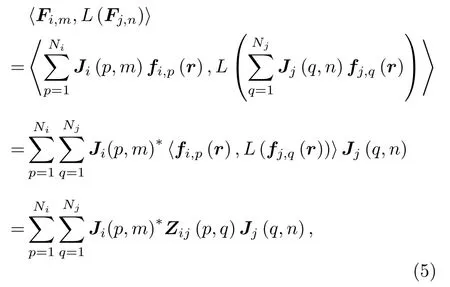
式中,Fi,m,Fj,n分 别表示子域i和j上的第m,n个 CBFs;fi,p(r) ,fj,q(r) 分别为子域i和j上的第p,q个 Rao-Wilton-Glisson (RWG)基 函 数.Zij(p,q)=Zpq=〈fi,p(r),L(fj,q(r))〉,Zij表示子域i和j上所有RWG基函数之间的相互作用,Zpq是第p个RWG基函数和第q个RWG基函数之间的相互作用.Ji(p,m) 为联系子域i中第m个CBFs和子域i中第p个RWG的线性标出系数, 这些系数构造矩阵Ji中的每一列对应一个 CBFs;Jj(q,n)为联系子域j中第n个 CBFs 和子域j中第q个RWG的线性标出系数,Ni和Nj分别表示子域i和j所包含的RWG基函数的数目.因此子域i和j所有CBFs之间的相互作用可以表示为

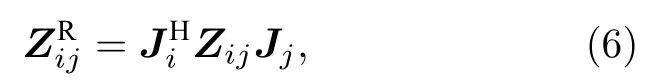
从(6)式和(7)式可以看出, 运用伽略金方法构造缩减矩阵时, 使用Ji的共轭转置同乘方程两边, 检验函数和基函数均采用CBFs(Ji).由(6)式和(7)式可得整个缩减矩阵方程的表达式为

通过求解(8)式即可得到系数矩阵α, 通常求解(8)式可以选择直接法求解, 但在分析电大复杂目标时, 缩减矩阵维数增大, 缩减矩阵方程需要通过迭代法求解.

3 新型缩减矩阵构造

为提高缩减矩阵方程迭代求解效率, 本文提出一种新型缩减矩阵构造方法, 首先应用SVD对激励矩阵进行压缩:

设定门限τ去除Ui中具有线性相关性的分量并将其表示为, 并将定义为激励基函数.假设每个子域经过SVD后包含Li个激励矢量, 将新的激励源代入到(1)式, 求解出每个子域的CBFs:

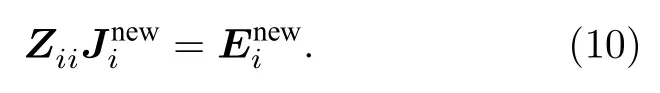
由于Li≪Npws, 可以显著减少方程求解次数.通过求解(10)式, 每个子域可得到Li个将分别作为构建缩减矩阵的检验函数和基函数, 则缩减矩阵子矩阵可以表示为

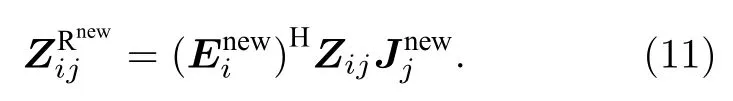
4 数值算例

为验证本文方法(novel characteristic basis function method, NCBFM)的有效性和精确性,分别对导体球、锥球带缝体的双站RCS以及杏仁体的单站RCS进行了计算.所有算例均在Intel(R) Core(TM) i5-6200U 2.30 GHz, 48 GB RAM 的PC 机上完成, 编译器采用Visual studio 2013, BiCGStab迭代误差为 0.001, 为了验证NCBFM计算精度, 定义电流系数均方根误差为

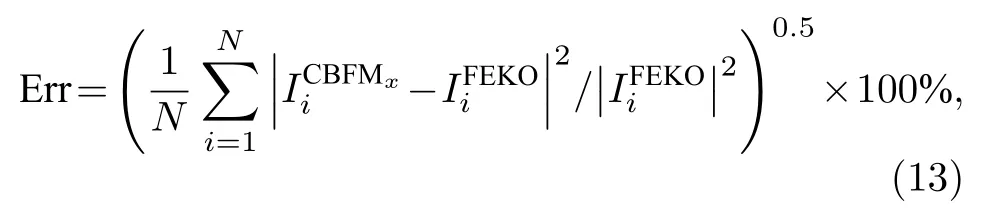
算例1计算一个半径为λ导体球的双站RCS, 入射频率为 300 MHz, 入射角度θ=0°,ϕ=0°.应用三角单元剖分球表面, 未知数为17278, 目标划为8个子域.NCBFM和CBFM均为每个子域构造800个激励, 图1(a)给出了2种方法在不同SVD门限下的电流误差以及CBFs数目.从图1(a)可以看出, 采用SVD压缩激励源, 电流误差收敛速度更快; 另外, CBFM在分析电大复杂目标时, 激励数目往往根据经验设定, 存在大量冗余计算, 而应用SVD对激励源进行压缩, 只需设置合适的SVD门限, 就可以在保证精度的情况下减少冗余计算.根据电流误差分析, CBFM和NCBFM的门限τ分别取0.005和0.008, 图1(b)给出了左半球面4个子域SVD后奇异值的分布曲线.从图1(b)可以看出, 2种方法在每个子域奇异值数目为80时即可达到门限设置要求, CBFM得到653个CBFs, 缩减矩阵维数为 6 53×653 , 矩阵条件数为5282, 采用BiCGStab迭代法求解缩减矩阵方程, 迭代26次即可收敛.NCBFM共得到649个CBFs, 缩减矩阵维数为 6 49×649 , 矩阵条件数为1785, 缩减矩阵方程迭代17次即可收敛,计算效率提高了34.6%.分别应用CBFM和NCBFM计算了导体球HH极化双站RCS, 计算结果如图1(c)所示, 从图1(c)可以看出,NCBFM与CBFM计算结果吻合较好, 计算精度较高.

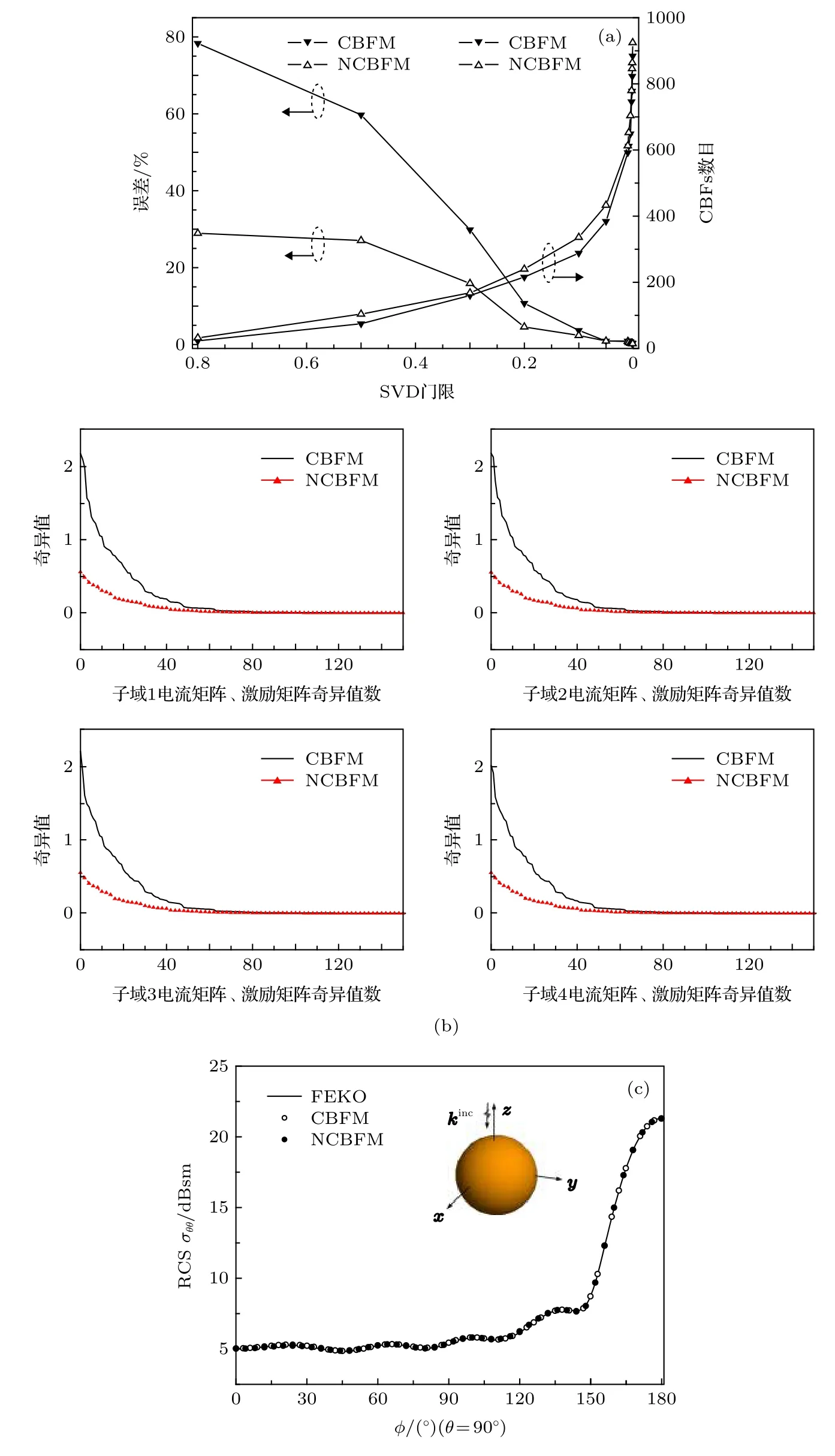
图1 (a)不同SVD门限下2种方法的计算误差及CBFs数目; (b)左半球面4个子域的奇异值分布曲线; (c)导体球双站RCSFig.1.(a) Calculation error and numbers of CBFs under different SVD thresholds of two methods; (b) singular value distribution curve in four sub-domains of the left hemisphere; (c) bistatic RCS of PEC sphere.

算例2计算一个锥球带缝体的双站RCS, 其几何外形定义见文献[28], 入射频率为6 GHz, 入射角度θ=270°,ϕ=0°.应用三角单元剖分目标表面, 得到124685个未知数, 目标被划为48个子域.2种方法在每个子域上均设置1600个激励, CBFM的SVD门限为0.001, 共得到7829个CBFs, 若采用直接法(LU分解)求解缩减矩阵方程需要耗时1239.6 s, 而采用迭代法求解缩减矩阵方程, 迭代86次即可收敛, 耗时104.5 s.NCBFM的SVD门限为0.002, 共得到7775个基函数, 缩减矩阵方程迭代求解45次即可收敛, 耗时57.3 s, 计算效率提高了45.2%.2种方法计算的HH极化双站RCS如图2所示, 从图2可以看出NCBFM计算的结果与CBFM和FEKO吻合较好.

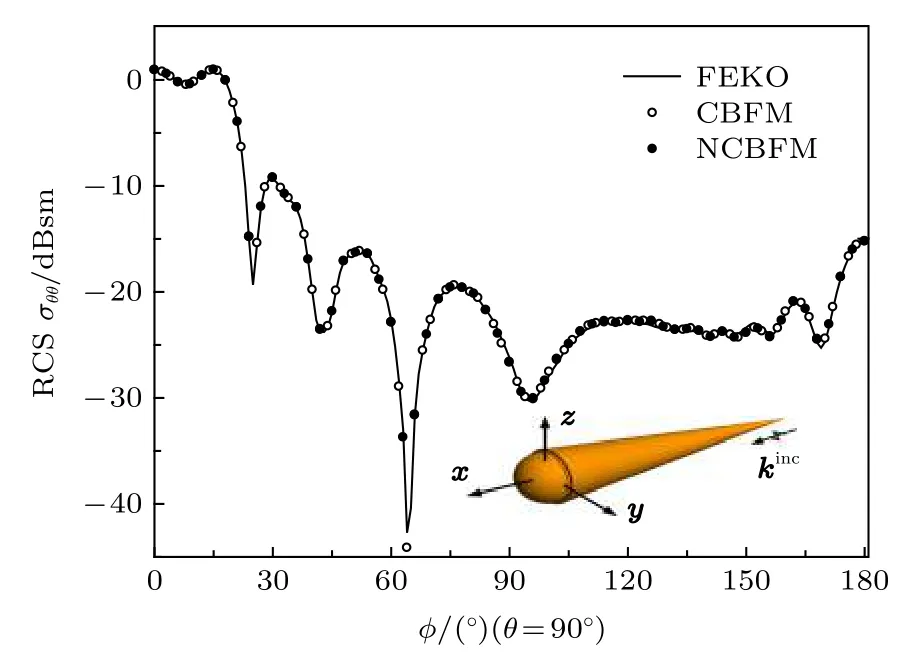
图2 锥球带缝体双站RCSFig.2.Bistatic RCS of cone-sphere with gap.

算例3计算一个252.3744 mm杏仁体的单站RCS, 入射频率为20 GHz, 入射角为θ=90°,φ=0°- 1 80°.用三角单元对目标表面进行剖分,共得到153690个未知数, 目标划为52个子域.2种方法设置的激励数均为1600, CBFM和NCBFM的SVD门限分别为0.001和0.002, 分别得到11410和11362个CBFs, 若采用直接法求解缩减矩阵方程, 需要耗时5387.3 s.应用CBFM求解缩减矩阵方程, 迭代次数平均为128.2, 单次缩减矩阵方程求解平均耗时237.8 s; NCBFM迭代次数平均为63.5, 迭代次数减少了50.4%, 单次缩减矩阵方程求解平均耗时121.2 s.图3给出了2种方法计算的HH极化单站RCS, 从图3可以看出, NCBFM的计算结果与FEKO吻合较好, 具有较高的计算精度.

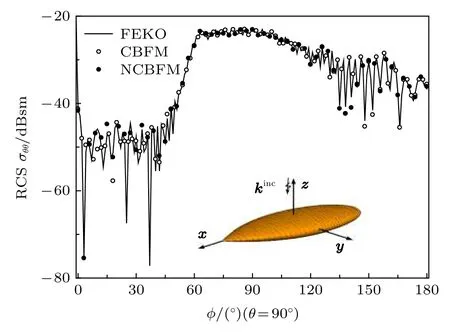
图3 杏仁体HH极化单站RCSFig.3.Monostatic RCS in HH polarization of NASA almond.

表1给出了CBFM和NCBFM在阻抗矩阵填充、基函数构造、缩减矩阵构造以及缩减矩阵方程时的求解时间.从表1可以看出, NCBFM在基函数构造方面计算效率有了小幅提高, 在缩减矩阵方程迭代求解方面计算效率都得到了显著提高.

5 结 论

本文给出了一种新型缩减矩阵构造方法, 该方法应用奇异值分解技术压缩激励源, 并在新激励源下求解出各子域的特征基函数, 减少了冗余计算;在构造缩减矩阵时, 选择激励基函数和特征基函数作为检验函数和基函数, 将缩减矩阵的对角子矩阵优化为单位矩阵, 提高了缩减矩阵方程的迭代求解效率.数值结果证明了本文方法在保证精度的前提下, 有效地提高了缩减矩阵方程的迭代求解效率.本文方法提高了缩减矩阵方程的迭代求解效率, 但在迭代过程中存在大量的矩阵向量积运算, 今后会进一步研究将多层快速多极子法、自适应积分法、预修正-快速傅里叶变换法、快速偶极子法等算法引入到该方法中, 加快矩阵向量积运算, 以提高特征基函数法分析电大目标电磁散射特性的效率.

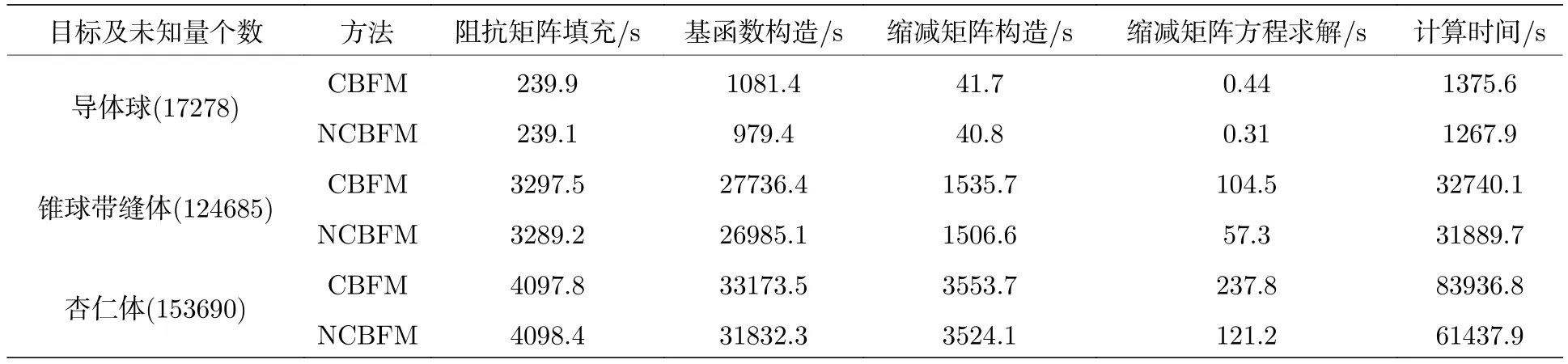
表1 计算时间比较Table 1.Comparison of computation time.