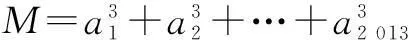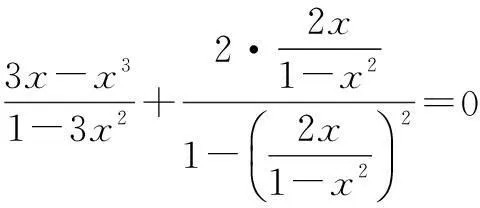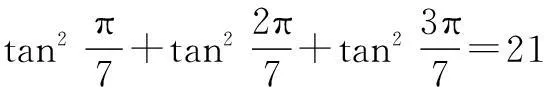例谈三倍角公式的应用
金国林
(浙江省宁波市镇海中学,315200)
○短文集锦○
例谈三倍角公式的应用
金国林
(浙江省宁波市镇海中学,315200)
正余弦函数的三倍角公式作为一个证明题出现在人教A版必修4习题3.1的B组中.尽管如此,由于平时运用公式解决问题的机会不多,学生对三倍角公式还是比较陌生的,有些问题也联想不到三倍角公式上去.但是三倍角公式却是许多试题的题源,受到高校自主招生和各类竞赛命题者的青睐.针对这种情况,笔者举例来简单谈谈公式的常见应用,以飨读者.
一、熟悉公式
容易证明三倍角公式:
sin 3x=3sin x-4sin3x;
cos 3x=4cos3x-3cos x;
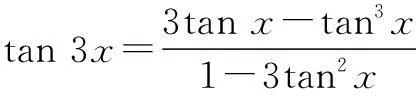
二、计算特殊角的三角函数值
例1计算sin 18°.
解由sin 54°=cos 36°,可得
3sin 18°-4sin318°=1-2sin218°,

评注学生一般对15°的倍数角的三角函数值非常熟悉.事实上,18°角也是一个非常重要的特殊角,在很多方面有很好的应用.
三、判断三角函数值的特性
例2证明tan 3°是无理数
评注本题是2014年北约自主招生试题.利用反证法,结合正切函数的三倍角公式,不难得到证明.
四、三角恒等式的化简、求值
例3化简下式:
解由sin 3θ=3sinθ-4sin3θ,得
=1+2cos 2θ.
评注将公式进行变形后运用,往往能取得意想不到的效果.
五、在三次方程中的应用
例4设函数f(x)=x3-3x+1有三个不同的零点α,β,γ,且α<β<γ,求证:β2-γ2=α-β.
证明由题意f(-2)<0,f(0)>0,f(1)<0,f(2)>0,
故α∈(-2,0),β∈(0,1),γ∈(1,2).

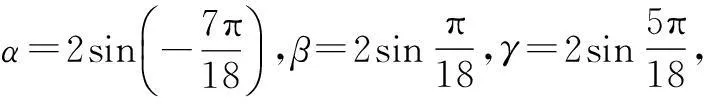
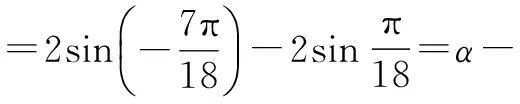
评注本题是一道2009年的匈牙利数学竞赛题.观察三次方程的系数特点,巧妙联系正弦三倍角公式,将方程的三个根以三角函数值的形式简洁表示,回避了繁杂的根式表达,大大简化了后续运算.
六、求解高次方程组
例5求出满足下面方程组的所有五元数组(x,y,z,v,w),其中x,y,z,v,w∈[-2,2].
解设x=2cosθ1,y=2cosθ2,z=2cosθ3,v=2cosθ4,w=2cosθ5,θi∈[0,π].
又cos 5θ=cos 2θcos 3θ-sin 2θsin 3θ
=16cos5θ-20cos3θ+5cosθ,
则2cos 5θ=(2cosθ)5-5(2cosθ)3
+5(2cosθ).
由题设条件,我们得2cos 5θ1+2cos 5θ2+2cos 5θ3+2cos 5θ4+2cos 5θ5=-10.
根据余弦函数的有界性,得
cos 5θ1=cos 5θ2=cos 5θ3=cos 5θ4
=cos 5θ5=-1,
评注本题利用常规的消元法处理有一定难度,不容易找到一个平衡点,利用多倍角公式的系数特点,可以从整体上快速得到解决.
七、命制试题的源泉
例6设函数f(x)=ax3-3x+1,若对于任意的x∈[-1,1]都有f(x)≥0成立,则实数a的值为______.
评注本题是2008年的江苏高考题,答案是a=4.本题主要考察利用导数处理含参函数的恒成立问题,有一定难度,需要很强的综合能力.事实上,本题的命制背景就是正弦函数的三倍角公式sin 3x=3sin x-4sin3x,熟悉公式的同学应该可以马上得到答案.
最后提供几个可以利用三倍角公式解决的练习,并附有提示,感兴趣的读者不妨尝试一下.

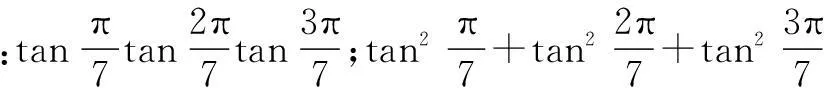
3.(2013年清华大学数学金秋营)已知函数f(x)=x3-3x+1.
(1)证明:函数f(x)有三个零点a (3)定义映射 f:(a,b,c)→{a,b,c},f(t)=t2-2, 求f(a),f(b),f(c). 练习提示 即x6-21x4+35x2-7=0. 3.提示:参考例4. 故M=2(cos 3θ1+cos 3θ2+…+cos 3θ2013)≤4 026. (2)证明:若x=t是f(x)的一个零点,则x=t2-2也是f(x)的一个零点;