高三数学综合测试



高三数学综合测试

一、填空题(本大题共14小题,每小题5分,共70分)

1.已知集合U={1,2,3,4,5},A={1,2,4},则UA=______.

2.已知复数z1=1+3i,z2=3+i(i为虚数单位)，在复平面内,z1-z2对应的点在第______象限.

3.命题:“∃x∈R,|x|≤0”的否定是______.

4.在平面直角坐标系xOy中,抛物线y2=8x上横坐标为1的点到其焦点的距离为______.

5.设实数x,y满足

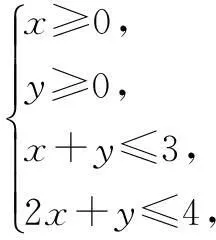
则z=3x+2y的最大值是______.

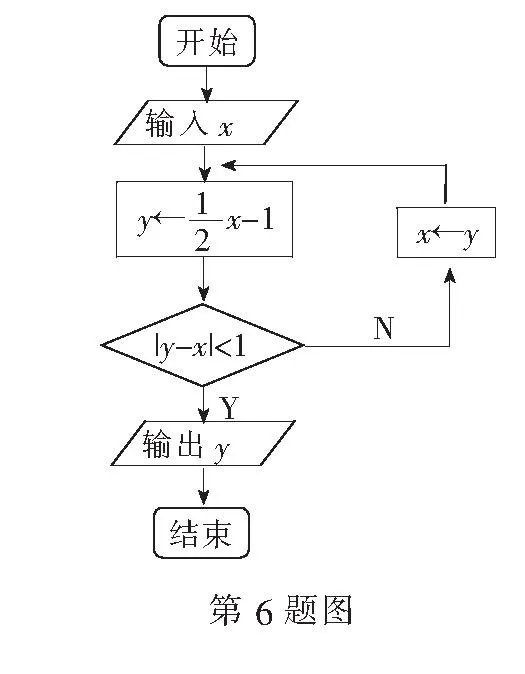
6.如图是一个算法的流程图，若输入x的值为2,则输出y的值是______.

8.抽样统计甲、乙两个城市连续5天的空气质量指数(AQI),数据如下:

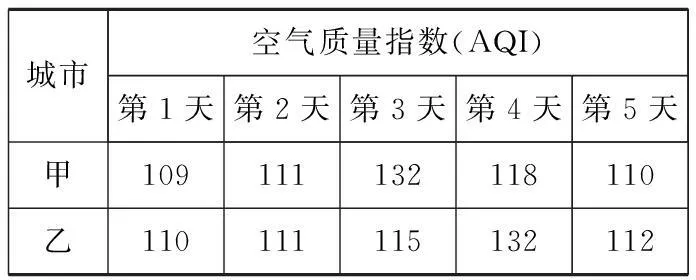
城市空气质量指数(AQI)第1天第2天第3天第4天第5天甲109111132118110乙110111115132112

则空气质量指数(AQI)较为稳定(方差较小)的城市为______(填甲或乙).

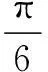
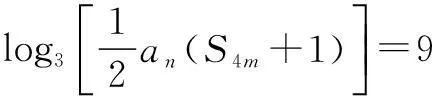
11.若向量a=(cosα,sinα),b=(cosβ,sinβ),且|a+b|≤2a·b,则cos(α-β)的值是______.

12.在平面直角坐标系xOy中,直线y=x+b是曲线y=aln x的切线,则当a>0时,实数b的最小值是______.

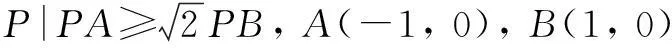
14.若函数f(x)=ax2+20x+14 (a>0)对任意实数t,在闭区间[t-1,t+1]上总存在两实数x1、x2,使得|f(x1)-f(x2)|≥8成立,则实数a的最小值为______.

二、解答题(本大题共6小题,共90分.解答时应写出文字说明、证明过程或演算步骤)

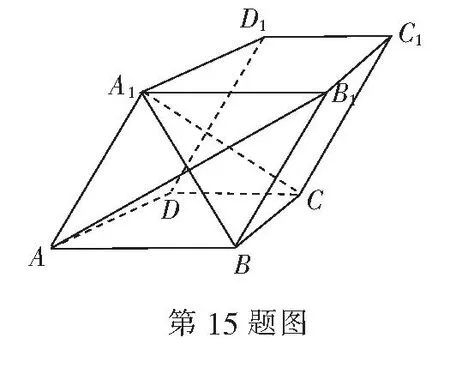
15.(本小题满分14分)如图,在四棱柱ABCD-A1B1C1D1中,AB∥CD,AB1⊥BC,且AA1=AB.

(1)求证:AB∥平面D1DCC1;

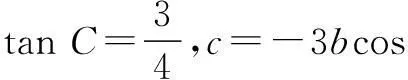
(1)求tan B的值;

(2)若c=2,求∆ABC的面积.

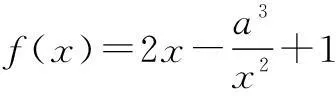
(1)求函数f(x)的单调区间;

(2)若f(x)≥a-1对一切x>0成立,求a的取值范围.

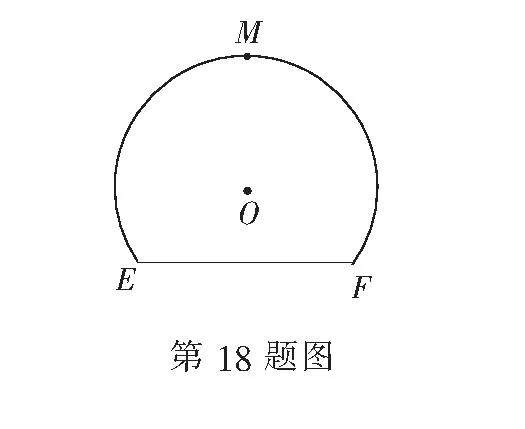
(1)求矩形铁片ABCD的面积S关于θ的函数关系式;

(2)当矩形铁片ABCD的面积最大时，求cosθ的值.

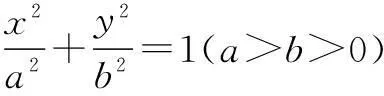
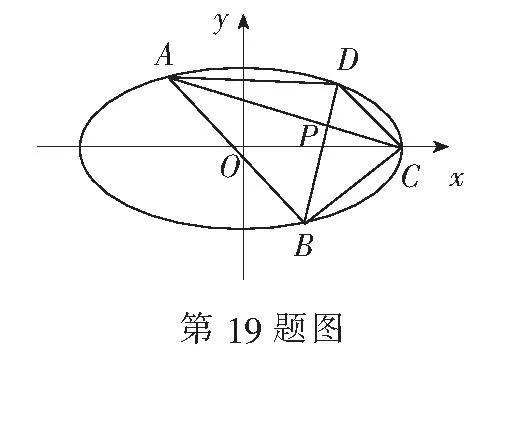
(1)求椭圆的方程;

(2)求直线AB的斜率.

20.(本小题满分16分)已知等差数列{an}、等比数列{bn}满足a1+a2=a3,b1b2=b3,且a3,a2+b1,a1+b2成等差数列,a1,a2,b2成等比数列.

(1)求数列{an}和数列{bn}的通项公式;

(2)按如下方法从数列{an}和数列{bn}中取项:

第1次从数列{an}中取a1,

第2次从数列{bn}中取b1,b2,

第3次从数列{an}中取a2,a3,a4,

第4次从数列{bn}中取b3,b4,b5,b6,

……

第2n-1次从数列{an}中继续依次取2n-1个项,

第2n次从数列{bn}中继续依次取2n个项,

……

由此构造数列{cn}:a1,b1,b2,a2,a3,a4,b3,b4,b5,b6,a5,a6,a7,a8,a9,b7,b8,b9,b10,b11,b12,…,记数列{cn}的前n和为Sn.求满足Sn<22014的最大正整数n.

参考答案

一、填空题

1.{3,5}；2.二；3.∀x∈R,|x|>0；

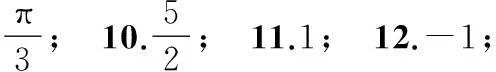
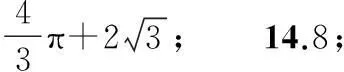
二、解答题

15.(1)在四棱柱ABCD-A1B1C1D1中,AB∥CD,AB⊄平面D1DCC1,CD⊂平面D1DCC1,

所以AB∥平面D1DCC1.

(2)在四棱柱ABCD-A1B1C1D1中,四边形A1ABB1为平行四边形,又AA1=AB,故四边形A1ABB1为菱形，从而AB1⊥A1B.

又AB1⊥BC,而A1B∩BC=B,A1B,BC⊂平面A1BC,所以AB1⊥平面A1BC.

16.(1)由正弦定理,得

sin C=-3sin Bcos A,

即sin(A+B)=-3sin Bcos A，

所以sin Acos B+cos Asin B=-3sin Bcos A，

从而sin Acos B=-4sin Bcos A.

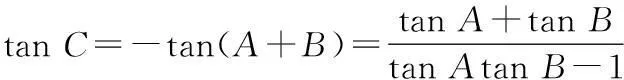
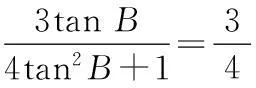
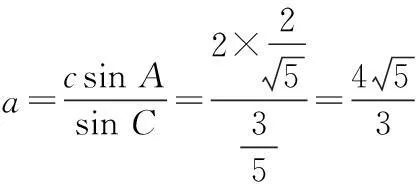
所以∆ABC的面积为

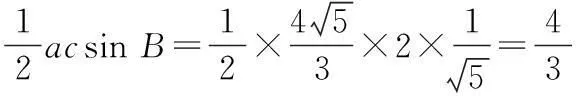
17(1)由奇函数的对称性可知,我们只要讨论f(x)在区间(-∞,0)的单调性即可.

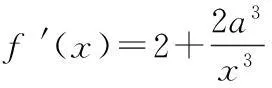
① 当a≤0时,f′(x)>0,故f(x)在区间(-∞,0)单调递增.

② 当a>0时,x ∈(-∞,-a),f′(x)>0,所以f(x)在区间(-∞,-a)单调递增.

x ∈(-a,0),f′(x)<0,所以f(x)在区间(-a,0)单调减.

综上所述，当a≤0时,f(x)单调增区间为(-∞,0),(0,+∞);当a>0时,f(x)单调增区间为(-∞,-a),(a,+∞),单调减区间为(-a,0),(0,a).

(2)因为f(x)为奇函数,所以当x>0时,

f(x)=-f(-x)

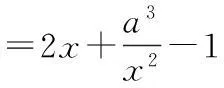
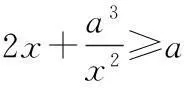
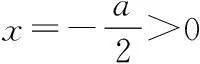
② 当a=0时,f(x)=2x-1>-1=a-1对一切x>0成立,故a=0满足题设要求.

③ 当a>0时,由(1)可知f(x)在(0,a)是减函数,在(a,+∞)是增函数.

所以f(x)min=f(a)=3a-1>a-1,所以a>0时也满足题设要求.

综上所述,a的取值范围是[0,+∞).

18.设矩形铁片的面积为S,∠AOM=θ.

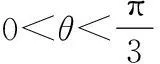
AB=4cosθ+2,AD=2×4sinθ,

S=AB×AD=(4cosθ+2)(2×4sinθ)

=16sinθ(2cosθ+1).

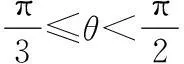
AB=2×4cosθ,AD=2×4sinθ,

故S=AB×AD=64sinθcosθ=32sin 2θ.

综上，得矩形铁片的面积S关于θ的函数关系式为

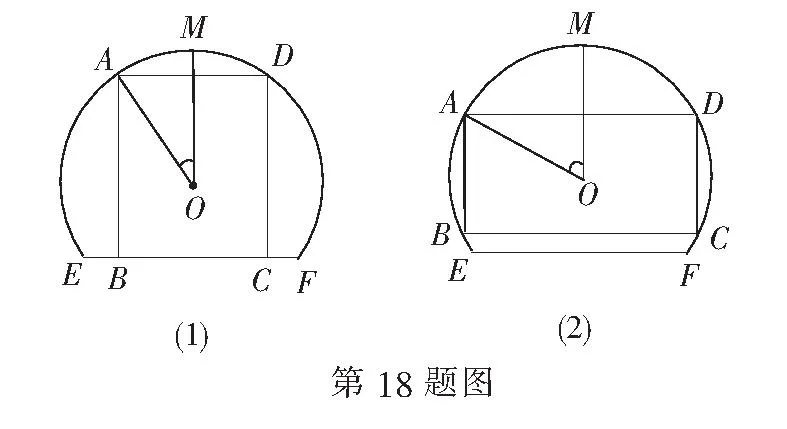
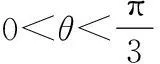
S′=16[cosθ(2cosθ+1)+sinθ(-2sinθ)]

=16(4cos2θ+cosθ-2)，

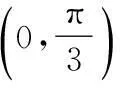
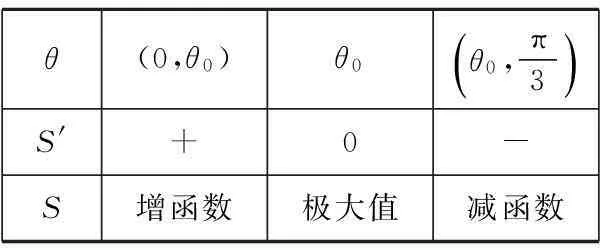
θ(0,θ0)θ0θ0,π3()S'+0-S增函数极大值减函数

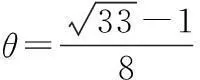
19.(1)依题意,有

解得a2=4,b2=1，

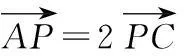
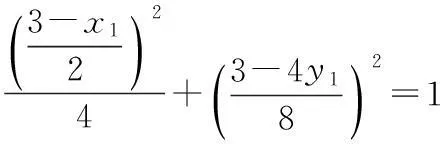
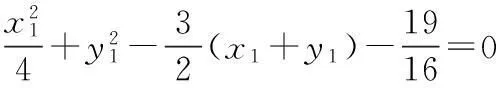
③

设B(x2,y2),同理可得

④

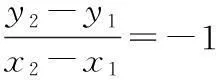
20.(1)设等差数列{an}的公差为d,等比数列{bn}的公比为q,依题意,得

解得a1=d=1,b1=q=2，

故an=n,bn=2n.

(2)将a1,b1,b2记为第1组,a2,a3,a4,b3,b4,b5,b6记为第2组,a5,a6,a7,a8,a9,b7,b8,b9,b10,b11,b12记为第3组,…以此类推,则第n组中,有2n-1项选取于数列{an},有2 n项选取于数列{bn},前n组共有n2项选取于数列{an},有n2+n项选取于数列{bn},记它们的总和为Pn,并且有

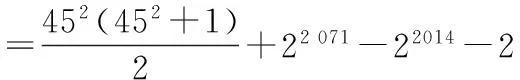
>0,

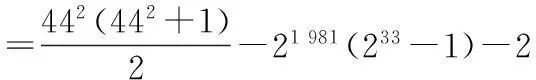
<0.

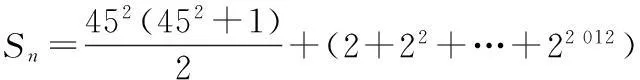
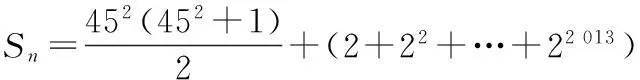
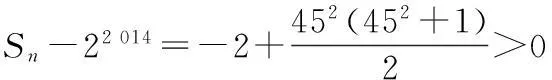
可得到符合Sn<22 014的最大的

n=452+2 012=4 037.

(2)求证:AB1⊥平面A1BC.