以高考题为例谈求解离心率问题的通性通法

陆修群

(江苏省如东县丰利中学，226408)



以高考题为例谈求解离心率问题的通性通法

陆修群

(江苏省如东县丰利中学，226408)

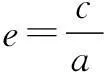
方法1根据已知条件构造a,b,c的等量关系求离心率的值．

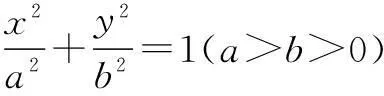
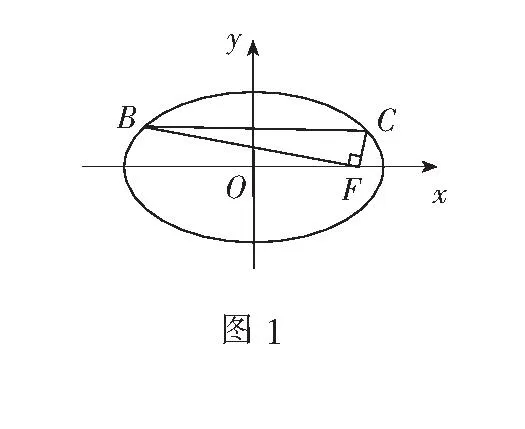
分析1根据已知条件求出具体的点B、C、F,结合∠BFC=90°，得到a,b,c的等量关系,求离心率的值．

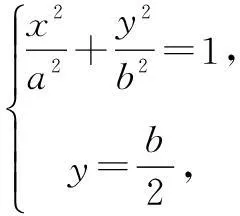
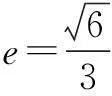
分析2设而不求,运用整体思想进行消元化简,进而得到a,b,c的等量关系求离心率的值．

解法2设C(x0,y0),B(-x0,y0),则

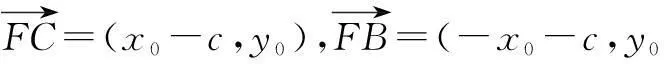
由∠BFC=90°，得

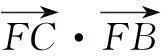
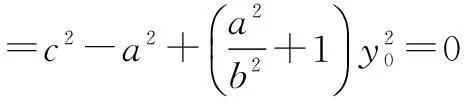
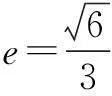
分析1根据双曲线的对称性，求出曲线E上矩形的一顶点A的坐标，代入双曲线方程即可.

方法2利用圆锥曲线的第二定义构造a,b,c的等量关系求离心率的值．

例2也可以运用方法2求解.

评注本题求点A坐标的过程不复杂(根据对称性结合图象很快可以求出)，但整个问题求解的思维过程远远大于计算量．

综观2016年各省离心率的计算问题,明显重视考查学生的思维过程,弱化在这类问题中的繁琐计算．圆锥曲线中的离心率的求值方法离不开上述的通性通法,即解决这类问题的关键是构造a,b,c的等量关系.一般情况下是利用已知(或者隐含的)条件构造等式,也可以通过探究曲线上的点的坐标(用a,b,c表示)代入曲线方程构造等式．