用基本不等式求最值为什么要“二定”
张 云
(江苏省华罗庚中学,213200)
○学习指导○
用基本不等式求最值为什么要“二定”
张云
(江苏省华罗庚中学,213200)
用基本不等式求最值是基本不等式的重要应用,也是高考的热点.基本不等式求最值要注意满足“一正二定三相等”这三个条件.其中,“二定”是三个条件中相当重要的条件,也是平时的考查点.由于学生对此较难理解,本文对此进行探索.
一、问题的提出
解法1∵x>0,
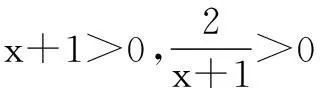

在课堂教学中,教师常常会给出上述解题过程,多数学生容易接受,但也有学生往往会提出如下解题思路:
所以当x=1,y取最小值2.
两种方法做的结果却不一样,学生百思不得其解.比较两种解法,为什么将表达式先加上1凑成根号下是乘积为定值.就可以求最值,难道解法2乘积不是定值就不能求最小值?对此,我们不妨从理论上加以探索.
二、解法探析
但解法2错误的根源是什么呢?我们再从理论上解决.先回顾函数最小值的定义:设函数y=f(x)的定义域为I,如果存在实数M满足:① 对于任意实数x∈I,都有f(x)≥M,② 存在x0∈I,使得f(x0)=M,那么,我们称常数M 是函数y=f(x)的最小值.这说明最小值一定是具体数值,这就是基本不等式求最值中“二定”的本质.从数形结合的角度看,f(x)在区间I内点x0处取最小值f(x0)=M,实质上就是要求y=f(x)在区间I内图象恒位于常值函数y=M图象上方,且两者在x0∈I处图象重合.再看看学生的做法:
当x>0时,由基本不等式知
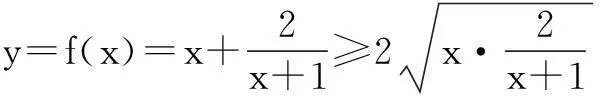

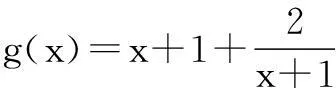
三、解题后的反思
我们总是责怪学生课堂听课效果差,殊不知是教师为了追求课堂的高效性少走弯路,对于基本不等式求最值的三个注意事项“一正二定三相等”,教师往往采用告诉式,这容易使学生听得云里雾里、似懂非懂,做练习时仍然犯上面的错误.再比如
例2设正数a,b满足a+b+3=ab,求a+b的最小值.
所以a+b=ab-3≥9-3-6(等号在a=b=3时取得),则a+b的最小值为6.

