例说外心问题的多角度切入
何振华
(江苏省海门中学,226100)
例说外心问题的多角度切入
何振华
(江苏省海门中学,226100)
在高三的各类模拟考试中,外心问题一直受到命题者的青睐,出现许多与外心有关的考题,而学生往往感到无从入手.本文以2015年我省泰州市的一道模考填空题为例,谈如何找到外心问题的切入点,意欲与大伙一起突破“外心”困惑.
试题在∆ABC中,D为边AC上一点,AB=AD=4,AC=6,若∆ABC的外心恰在线段BD上,则BC=______.
分析在∆ABC中,已知AB=AD=4,AC=6,只需求出∠BAC,即可用余弦定理求出BC.因此本题的思维障碍在于怎么求∠BAC,那么如何运用条件“∆ABC的外心恰在线段BD上”就显得十分重要.
角度1利用 “圆心角等于圆周角的2倍”,突破思维障碍
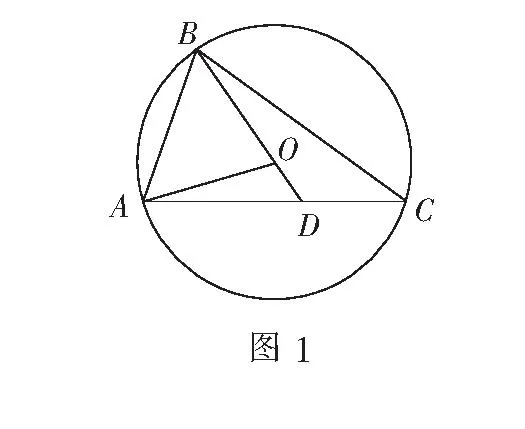
解如图1,设O为∆ABC的外心,∠BAC=θ,则∠AOB=2∠C.
因为AB=AD,所以
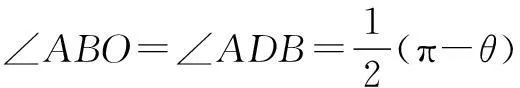
又AO=BO,所以
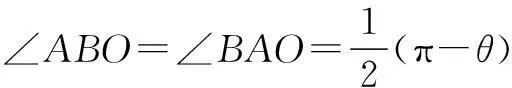
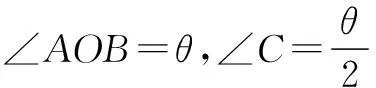
在∆ABC中,由正弦定理,得
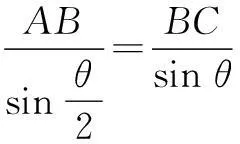
又BC2=62+42-2·6·4cosθ
=52-48cosθ.
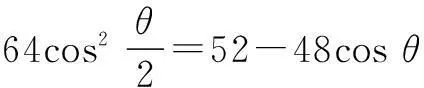
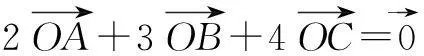
角度2利用 “中垂线”,突破思维障碍
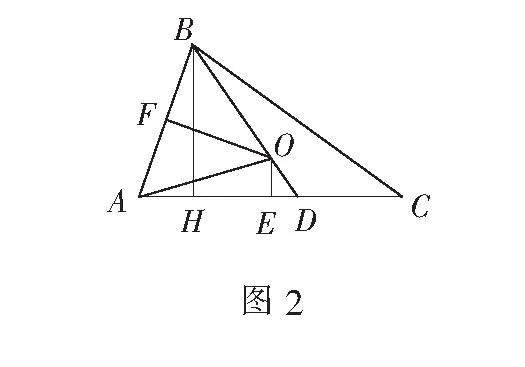
解如图2,取AC,AB中点E,F,连OE,OF,则OE⊥AC,OF⊥AB.
因为AB=AD,所以∠ABO=∠ADB,
所以Rt∆OED与Rt∆OFB相似,得

过点B作BH⊥AC于点H,则
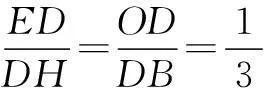
又ED=1,所以
DH=3,AH=4-DH=1.
评注外心是中垂线的交点这一特征可以帮助我们确定外心位置,将动态问题静态化,处理外心问题时,往往可以另辟蹊径,快速突破思维障碍.
角度3利用“圆方程”,突破思维障碍
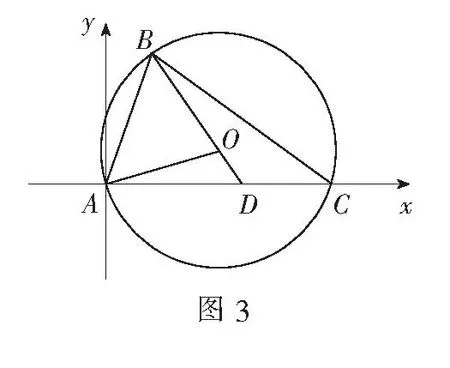
解如图3,以A为原点建立直角坐标系,则C(6,0),D(4,0).
设∠BAC=θ,则B(4cosθ,4sinθ),
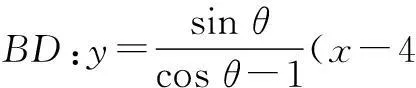
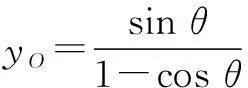
由题意,设外接圆方程为
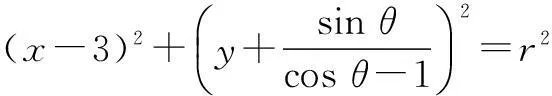
所以
评注利用圆方程求解,可以将几何问题代数化,往往可以降低问题的思维难度,回归解析几何的本质,可以帮助我们更快的找到问题的切入点.
角度4利用“AO=BO=CO”,突破思维障碍
解因为B,O,D三点共线,所以

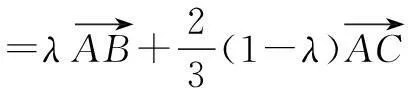
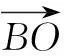
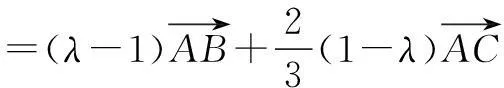
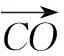
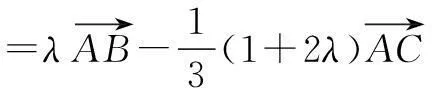
又AO=BO=CO,
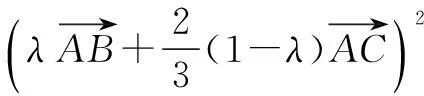
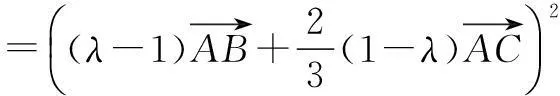
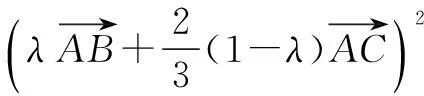
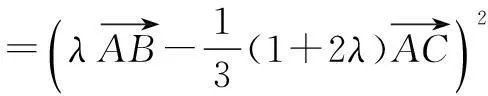
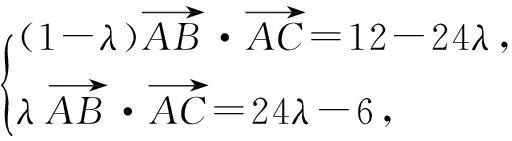
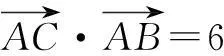
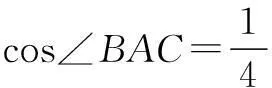
解因为B,O,D三点共线,所以
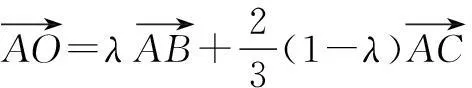
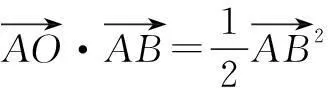
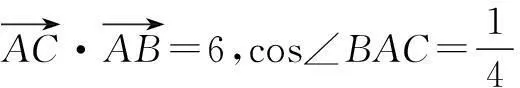
总的来说,如果你能从外心的特征出发,借助平面几何、解析几何、解三角形和向量知识,那么就能举一反三,找到外心问题的切入点,突破外心问题的困惑,玩转“外心”.
○解题思路与方法○

