通过一道习题谈数学解题方法
付长兵
(江苏省昆山中学,215300)
通过一道习题谈数学解题方法
付长兵
(江苏省昆山中学,215300)
数学解题的思维过程是指从理解问题开始,经过探索思路、转换问题直至解决问题,可简要概括为:理解、转换、实施、反思.
在高三复习的过程中,为了能够让学生迅速寻找到解决问题的方向,老师通常强调对一类问题的通性、通法,过于强调题型、方法,忽视了知识点之间的联系,对学生学习的主动性以及综合能力的培养会存在不利的影响.为了使回想、联想、猜想的方向更明确,思路更加活泼,进一步提高探索的成效,我们必须掌握一些解题的策略.笔者认为,从不同角度分析解决问题的方式方法,不仅能够激发学生学习的兴趣,还能够使学生更加清晰地串联起不同知识间关系,更有利于训练培养学生分析、转化问题以及解决问题的能力.
下面通过一道习题谈一谈数学解题过程中的策略与方法.
从结构上来分析,任何一道解答题,都包含条件和结论(或问题)两个方面.当我们面临的是一道以前没有接触过的陌生题目时,要设法把它化为曾经解过的或比较熟悉的题目,以便充分利用已有的知识、经验或解题模式,顺利地解出原题.

一、从结论出发,顺藤摸瓜
本题是计算三角形内角的大小,这让我们第一时间联想到了解三角形问题.又因为条件中出现了AB,AD,BD的长度,利用余弦定理求角的大小是我们熟悉的题型和方法,于是可以引导学生从余弦定理出发探索解题的过程.
解法1在∆ABD中,由余弦定理,知

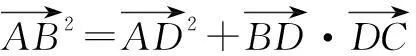
∴AB2-AD2=BD·DC,


又在∆ABC中,


∴AB=AC,
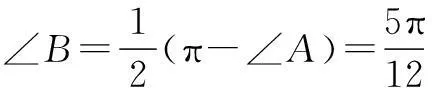
评注分别在两个三角形中利用余弦定理找到AB与AC的关系是本题的难点.从结论出发锁定解决问题的方法,这是遇到综合题时常用的思考方式.这种方法建立在对基本问题熟练掌握的基础之上,通过对条件的不断加工达到预期的目的.
二、从条件出发,直捣黄龙


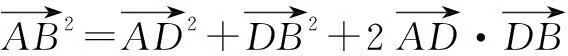
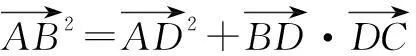
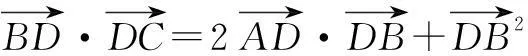

评注这种解法需要学生具备一定的综合探索能力,在确定了解题方法之后要勇敢地走下去.这跟下棋类似,我们有时看不到最后一步的结局,但在下棋的过程中我们逐渐看清了形势的发展,通过不断的调整取得最后的成功.
三、数形结合,轻而易举

AB2=AD2+BD·DC.
通过平方差公式,转化为形象鲜明、直观具体的几何问题得以解决.
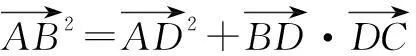
∴AB2=AD2+BD·DC.
∴(AB+AD)(AB-AD)=BD·DC.
延长DA至E,使得AE=AB,延长AD至F,使得AF=AB,则
DE·DF=BD·DC,
从而B、E、C、F四点共圆(如图2).


评注有些数学题,内容抽象,关系复杂,给理解题意增添了困难.对于这类题目,可以给题中有关数量以恰当的几何分析,拓宽解题思路,找出简捷、合理的解题途径.本题通过构造图形,巧妙利用四点共圆得以解决.
从这道题的解决过程中,我们可以发现,无论是从问题的条件出发还是从结论出发,在探索解题思路的过程中都需要在理解问题的基础上对熟悉的问题进行转化、加工,这是对基础知识和基本技能的灵活运用的过程.而这些能力的培养除了老师有意识地引导之外,更需要学生对每一个问题进行认真反思总结.它是发展数学思维的一个重要方面,是一个思维活动过程的结束包含另一个新的思维活动过程的开始.

