从一道高考题谈极化恒等式的应用

刘明明

(江苏省如东高级中学，226400)



○高考之窗○

从一道高考题谈极化恒等式的应用

刘明明

(江苏省如东高级中学，226400)

向量的数量积作为江苏高考的C级考点,是高考的核心考点之一．在处理数量积问题的过程中,一些重要结论的使用能促使问题更好更快地得到解决.本文从2016年江苏数学高考第13题出发,探索极化恒等式在解数量积问题中的应用．

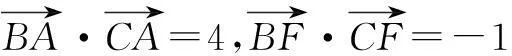
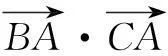
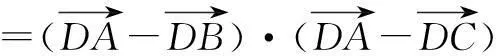
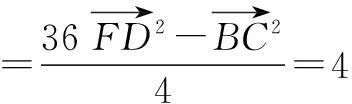
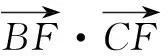
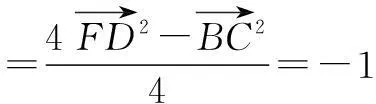
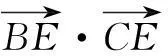
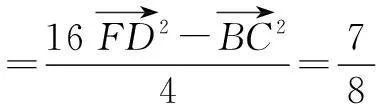
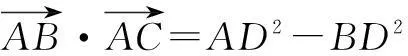
从极化恒等式可以看到向量的数量积可直接转化为几何长度问题,对研究向量的数量积问题有很大的帮助.笔者列举几例如下:

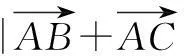
解连结BC,取BC的中点D，则

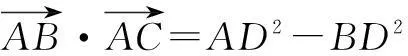
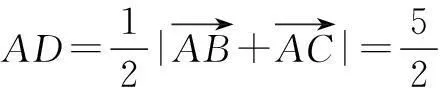
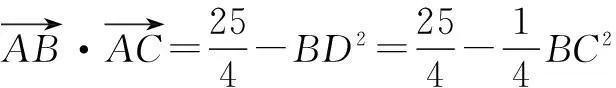
又因为BCmin=3-1=2,所以

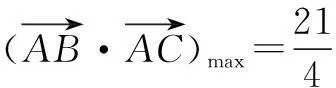
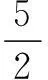
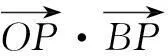
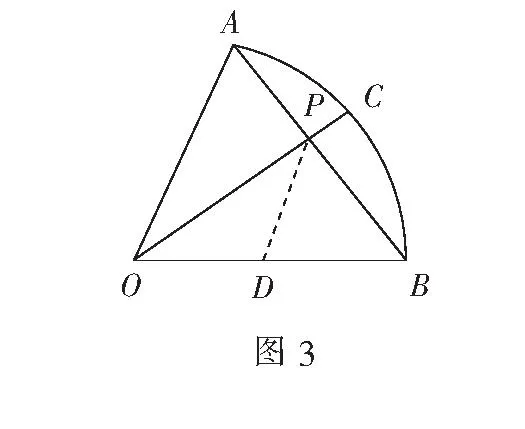
解如图3，取OB的中点D,连结PD，则

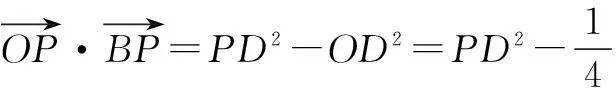
于是只要求PD的最小值即可．

由图3可知，当PD⊥AB时，

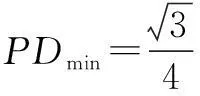
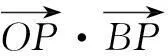
评注例2与例1都是通过将数量积的最值问题转化为几何线段的最值问题,极化恒等式从中起到重要的桥梁作用，但区别在于例2将数量积的最值问题转化为相应三角形的中线长最值问题．此外，例2中求PD的最小值还可以看成“以D为圆心的圆与线段AB有公共点,求圆半径最小值”．从这种角度看较典型的是下面的例子.

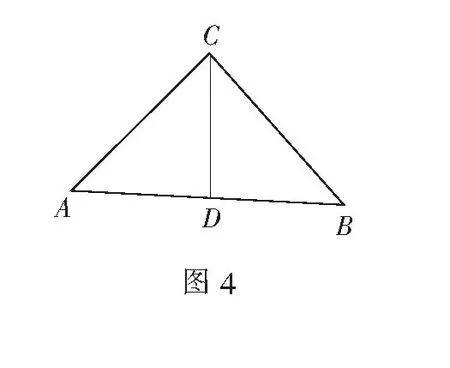
解如图4,取AB的中点D,连结CD，

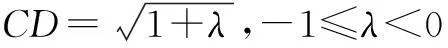
以上三题都是求最值问题,但问题也可以从“已知向量数量积的最值求相关参数”的角度发问,比如下面的例子.

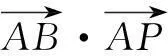
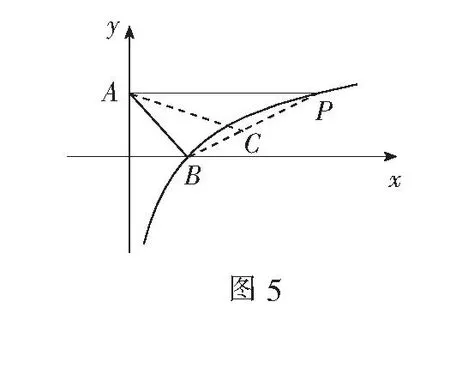
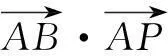
上式等价于AB2+BC2≤AC2,即∠ABP≥900当且仅当P与B重合时,取等号.

此时曲线C在B处的切线斜率为1,即

从前面的题目,我们看到极化恒等式对研究共起点(终点)向量数量积问题有很大的帮助.此外，对于有些不是共起点(终点)向量数量积问题,也可以用极化恒等式来探索．

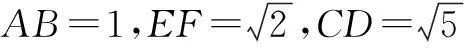
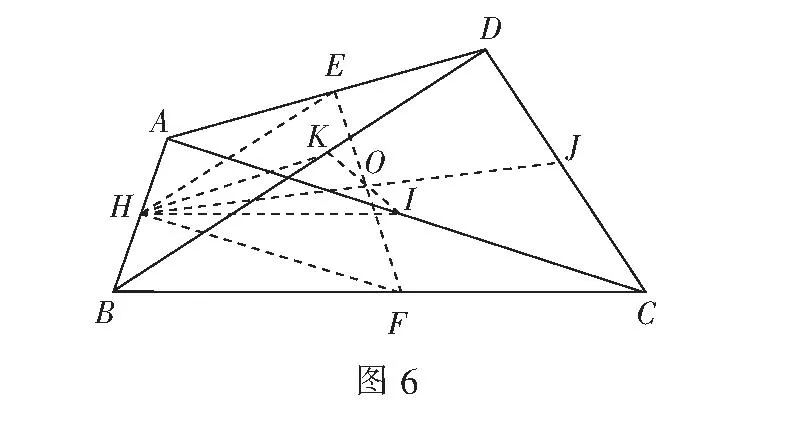
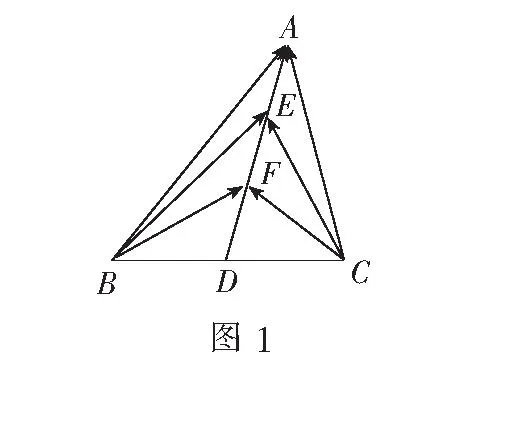
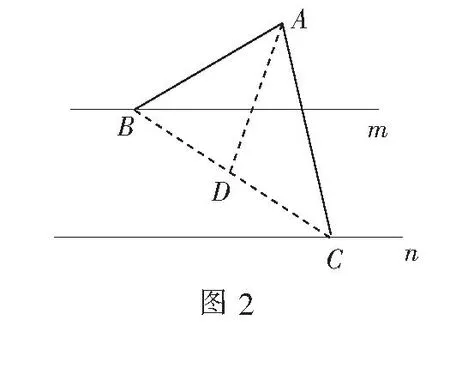
解如图6,取AB,AC,CD,BD中点H,I,J,K.

四边形ABCD中,易知EF,KI,HJ三线共点于O.

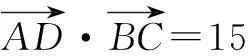
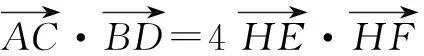
=4(HO2-FO2).

在∆EFI中,

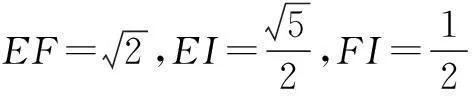
HO2=4.

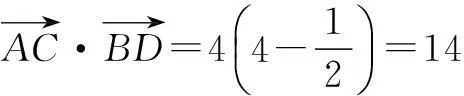
近几年来,对向量数量积的考查在一些模拟考试与高考中相当热门,而这些数量积问题基本上可以借助极化恒等式快捷地解决,故在平时教学中需要向学生渗透极化恒等式,让学生明白极化恒等式不仅是一种基向量思想的公式化表达方式,而且在解决向量数量积问题中有广泛的应用．