利用集合思想求解含参数线性规划问题
张 生 苏 猛
(内蒙古师范大学附属中学,010020)
利用集合思想求解含参数线性规划问题
张生苏猛
(内蒙古师范大学附属中学,010020)
线性规划是运筹学中研究较早、发展较快、应用广泛、方法较成熟的一个重要分支.它是辅助人们进行科学管理的一种数学方法,广泛地应用于军事作战、经济分析、经营管理和工程技术等方面.
简单线性规划问题实为二元函数(线性目标函数)在定义域内(线性约束条件)的最值问题.将定义域和函数置于图形之中,以形助数是高中阶段解决该类问题的主要手段.
在高考中,此类问题大致可分为简单线性规划问题,含参数线性规划问题,整数线性规划问题和非线性规划问题四大类.其中,含参数线性规划问题是学生不易理解掌握的一类,也是高考考察的趋势.下面,以高考题为实例,给出解决该类问题的一种集合视角下的解题方法,此法可以有效回避分类讨论.
一、问题模型及重要结论
问题模型目标函数max(min) z=ax+by(a,b∈R).
约束条件 a1x+b1y≥(≤,<,>)c1,
a2x+b2y≥(≤,<,>)c2,
……
anx+bny≥(≤,<,>)cn.
上述问题模型称为简单线性规划问题,其实质为在给定约束下,求二元函数的最值问题.这仅是规划问题中最为简单的情形,解决该类问题的主要方法是数形结合.关于问题模型,易得以下常用结论:
结论1记二元一次不等式组对应的平面区域为集合Ω,若Ω为一个封闭区域,则对(x,y)∈Ω,函数f(x,y)既有最大值,也有最小值.
结论2对(x,y)∈Ω(其中,Ω为二元一次不等式组对应的平面区域),若函数f(x,y)既有最大值,也有最小值,则Ω为一个封闭区域.
结论3函数f(x,y)的最大值和最小值只能在可行域的边界或顶点处取得.
结论4记二元一次不等式组对应的平面区域为集合Ω1,二元一次不等式对应的平面区域为集合Ω2,若Ω1⊆Ω2,则∀ (x,y)∈Ω1,都能使这个二元一次不等式成立.
结论5记二元一次不等式组对应的平面区域为集合Ω1,二元一次不等式对应的平面区域为集合Ω2,若Ω1∩Ω2≠∅,则∃ (x,y)∈Ω1,使这个二元一次不等式成立.
结论6当B>0时,不等式Ax+By+C>0解集对应的平面区域在直线Ax+By+C=0的上方;不等式Ax+By+C<0解集对应的平面区域在直线Ax+By+C=0的下方.
二、例题及解法探究
(*)
时,1≤ax+y≤4恒成立,则实数a的取值范围是______.
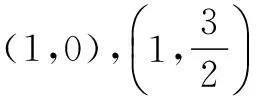
这一解法充分利用了结论2和结论3,是一种快速有效的解题办法,体现的是对问题的全面分析能力和解题技巧与策略的优化.
解法2记不等式组(*)对应的平面区域为Ω1,不等式组1≤ax+y≤4对应的平面区域为Ω2,由题意,∀(x,y)∈Ω1,都满足1≤ax+y≤4,利用结论4,知Ω1⊆Ω2.
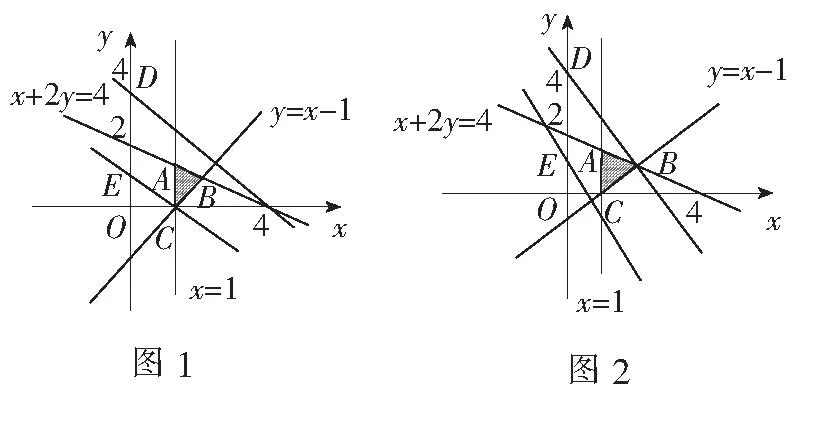

这一解法充分利用了结论4和结论6,将题干信息“当实数x,y满足(*)时,1≤ax+y≤4恒成立”转化为集合的包含关系,借助图象解题,充分体现划归与转化思想和数形结合思想.
(*)
如果目标函数z=x-y的最小值为-1,则实数m等于()
(A)7(B)5(C)4(D)3
解将问题转化为“对任意(x,y)满足(*)都有x-y≥-1成立”.记不等式组表示的区域为Ω1,不等式x-y≥-1表示的区域为Ω2,则有Ω1⊆Ω2,作图如图3.
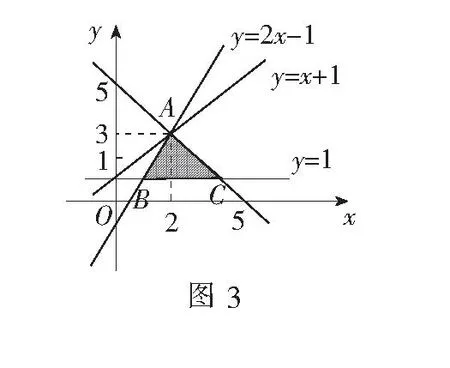
评注将题设“目标函数z=x-y的最小值为-1”转化“不等式x-y≥-1”.进而将规划问题转化为恒成立问题,利用集合的包含关系解题,这针对含有参数的规划问题的求解非常有效,可回避对参数的分类讨论.
但需要注意的是,若将题设条件改为“已知实数x,y满足(*),如果x-y≥-1恒成立”则m就不是具体值了,而是一个范围了,应为2≤m≤5. 若将题设条件改为“已知实数x,y满足(*),如果存在目标区域内的点(x,y)使得x-y≥-1成立”则m的范围应为m≥2.教学中,应注重此类问题的变式训练.

解由“z=ax+2y仅在点(1,0)处取得最小值”可得zmin=a,所以有ax+2y≥a.记约束条件表示的区域为Ω1,不等式ax+2y≥a表示的区域为Ω2.
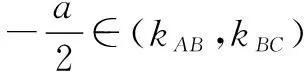
评注利用交集思想解决规划问题,借助图象,直观明了.此法关键在于将题设“目标函数z=ax+2y仅在点(1,0)处取得最小值”转化为“不等式ax+2y≥a”,进而将问题转化为两个平面区域(两个点集)相交问题.
类似问题在高考中出现频率很高(如2014山东,2014北京,2014湖南,2013新课标Ⅱ,2013大纲,2013浙江等),如何提高这类问题的解题能力?需要平时深入研究,得出解决问题的通性通法,并达到“做一题,会一类”的解题效应.

