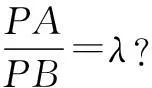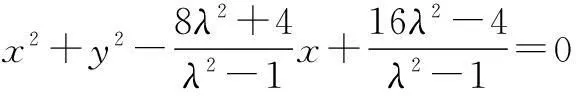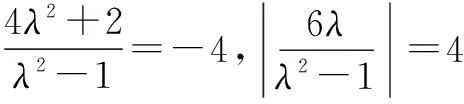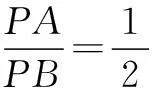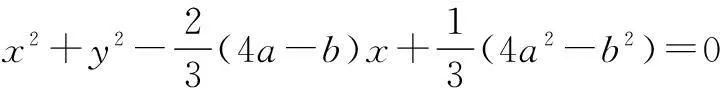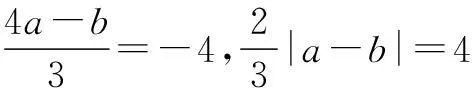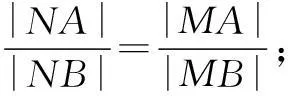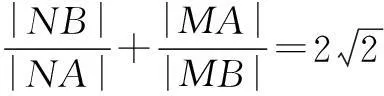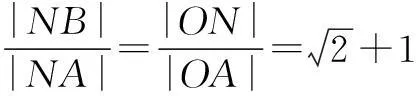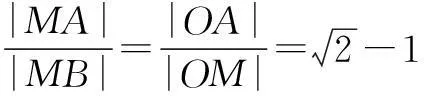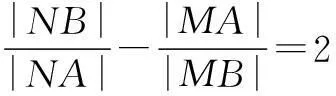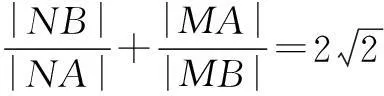阿波罗尼斯圆的探究及其应用
周顺钿
(浙江省杭州高级中学,310003)
○数学探究○
阿波罗尼斯圆的探究及其应用
周顺钿
(浙江省杭州高级中学,310003)
一、问题背景
我们知道,到两定点的距离之和为定值(定值大于两定点间的距离)的点的轨迹是椭圆,到两定点的距离之差为定值(定值大于零且小于两定点间的距离)的点的轨迹是双曲线.那么,到两定点的距离之商为定值(定值大于零且不等于1)的点的轨迹是什么呢?这就是由公元前3世纪下半叶古希腊数学家阿波罗尼斯(Apollonius of Perga,公元前262-公元前190)提出的几何作图问题,载于他的《论接触》中,惜原书已失传.
若避开纯几何解决方法,我们从解析法探究:设两个定点的坐标为A(-a,0),B(a,0),动点P的坐标为(x,y).
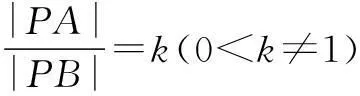
(x+a)2+y2=k2[(x-a)2+y2],
展开化简,得
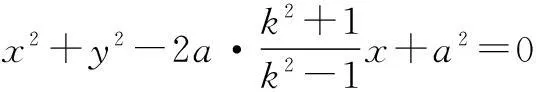
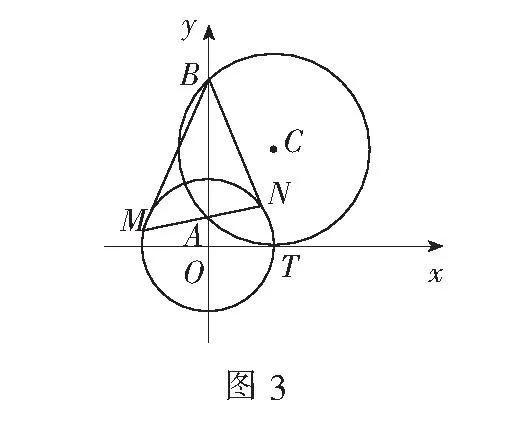
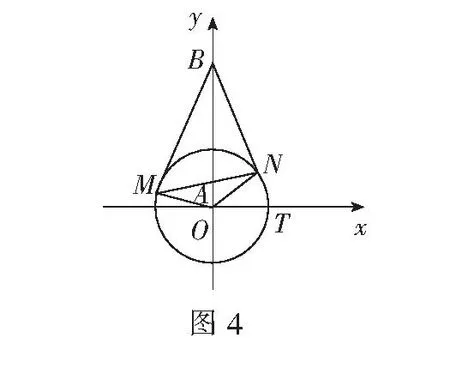
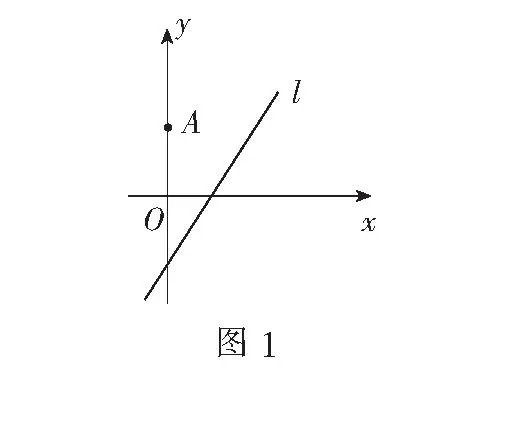
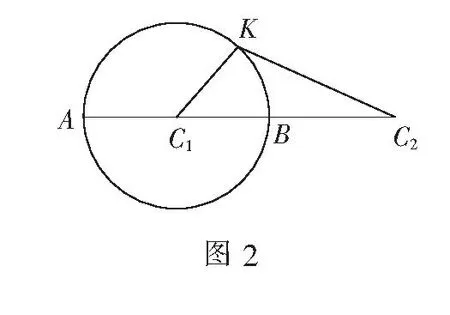
于是,平面内到两个定点的距离之比为常数k(0 现行中学数学教材在编写时都十分重视对数学历史题材的挖掘和应用.如,苏教版数学选修2-1在第二章《圆锥曲线和方程》第63页例2:“求平面内到两定点距离之比等于2的动点M的轨迹方程”就是对阿波罗尼斯圆的开发与应用. 例1在直角坐标平面上,已知点A(0,2),B(0,1),D(t,0)(t>0).点M是线段AD上的动点,如果|AM|≤2|BM|恒成立,求正实数t的最小值. 评注本题的关键是将问题转化为直线与圆的位置关系. 例2(2013年江苏高考题)如图1,在平面直角坐标系xOy中,点A(0,3),设圆C的半径为1,圆心C在直线l:y=2x-4上. (1)若圆心C也在直线y=x-1上,过点A作圆C的切线,求切线的方程; (2)若圆C上存在点M,使|MA|=2|MO|,求圆心C的横坐标a的取值范围. 解(1)所求切线方程为y=3或者3x+4y-12=0.(过程略) (2)设M(x,y),由|MA|=2|MO|,可得点M的轨迹为阿波罗尼斯圆 D:x2+(y+1)2=4. 由题意,点M应该既在圆C上又在圆D上,即圆C和圆D有公共点.设圆心C(a,2a-4),则 ≤|2+1|, 评注解决本题(2)的关键是转化为两圆的位置关系. 解由点M知,∠AKC=∠BKC, 即KC为∠AKB的平分线(如图2),所以 记A(-a,0),B(a,0),K(x,y),其中a>0,则点K的轨迹为阿波罗尼斯圆 当且仅当r=2时取等号. 评注本题通过对隐晦条件的层层剖析,揭示了点K的轨迹即为阿波罗尼斯圆,于是问题的背景便豁然开朗. 对于阿波罗尼斯问题,如果给予定点、定值、圆心、半径等相关的要素进行不同的组合,还可以作进一步的探究. 解设P(x,y),则 (x+2)2+y2=λ2[(x-4)2+y2], 展开化简得 与圆C:(x+4)2+y2=16相比较,得 4[(x-a)2+y2]=(x-b)2+y2, 化简得 评注上述两题本质上是阿波罗尼斯圆的逆向探究问题. 例6(2015年湖北高考题)如图3,圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2. (1)圆C的标准方程为______. (2)过点A任作一条直线与圆O:x2+y2=1相交于M,N两点,下列三个结论: 其中正确结论的序号是______.(写出所有正确结论的序号) OA·OB,故∆OAN∽∆OBN,从而∠ONA=∠OBN. 同理,∆OAM∽∆OBM,得∠OMA=∠OBM(如图4). 又由OM=ON,得∠OMA=∠ONA,于是∠OBM=∠OBN. 所以②③也成立. 数学探究教学是数学知识“再创造”和“再现”的重要方式.在探究活动中,教师应把自己的精力放在鼓励学生观察分析、自主探索和合作交流上.开放性是探究学习的一个重要特征,教师应创建一个开放的课堂教学体系,给学生营造一个宽松、和谐、民主的心理氛围,不限制学生思考问题的方向和角度,不预设探究的结果和产物,从而保证探究活动的有效性.二、阿波罗尼斯圆的灵活应用举例
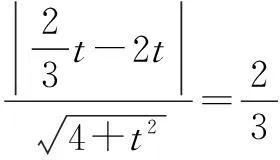
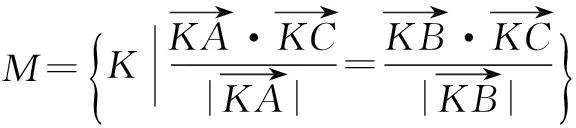

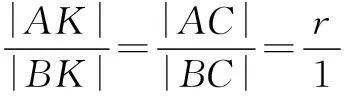
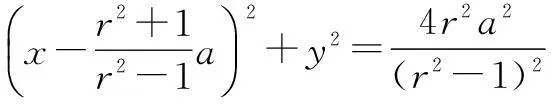
三、对阿波罗尼斯问题的进一步探究