以平面向量为背景的数列问题

庞良绪

(上海市市西中学,200040)



以平面向量为背景的数列问题

庞良绪

(上海市市西中学,200040)

平面向量作为代数与几何的纽带,具有代数与几何的双重身份,素有“与解几交汇,与立几联姻,与代数牵手”之美称.平面向量与数列问题的综合及应用通常涉及到向量夹角、平行、垂直、共线、共点等问题的处理,目标是将问题坐标化,符号化,数量化,从而将推理转化为运算.以平面向量为背景的数列问题由于综合性较强,因此对培养学生的发散性思维和创新意识都有一定的帮助.

一、以向量夹角为背景构造等比数列

(1)求向量an+1与an的夹角;

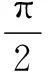
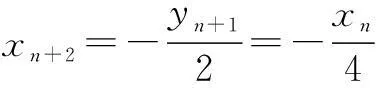
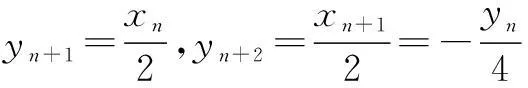
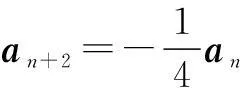
∴a1∥a3∥a5∥a7∥…

令b1=a1,b2=a3,…,bn=a2n-1(n∈N*)，显然

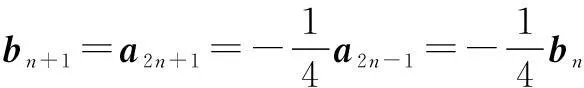
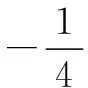
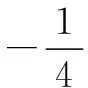
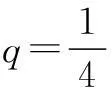
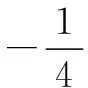
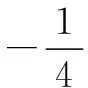
解(1)∵ |an+1|

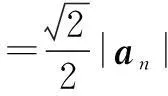
∴数列{|an|}是等比数列.

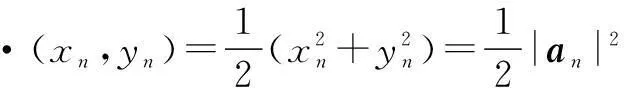
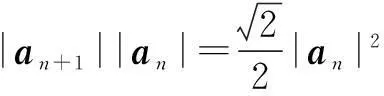
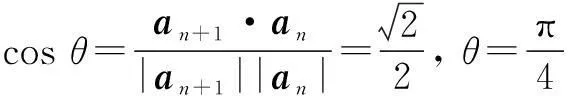
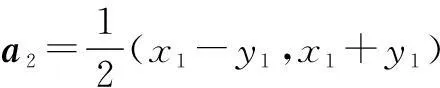
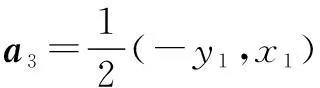
∴a1∥a5∥a9∥a13∥….

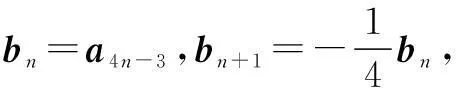
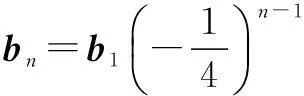
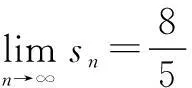
借助图象及相邻两向量夹角,知a1∥a5∥a9∥a13∥…，且a1、a5、a9、a13、…相邻两个向量方向相反,

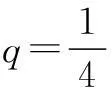
二、以向量垂直为载体，构造等差数列

例2已知Sn为数列{an}的前n项和,a=(Sn,1),b=(-1,2an+2n+1),a⊥b.

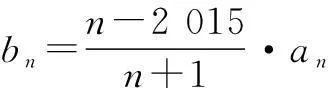
解(1)∵a⊥b,

∴-Sn+2an+2n+1=0，

①

-Sn+1+2an+1+2n+2=0.

②

①-②，得an+1=2an-2n+1,

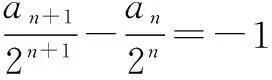
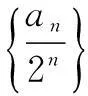
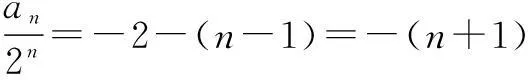
∴an=-(n+1)·2n,

∴bn=(2 015-n)·2n.

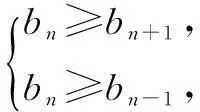
∴2 013≤n≤2 014,

∴bn的最大项为b2 013=b2 014,

∴n0=2 013或2 014.

评注本题关键衔接转换点是由a⊥b得a·b=0,建立Sn与an的关系式.

三、以共线向量为纽带巧得三点共线

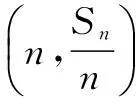
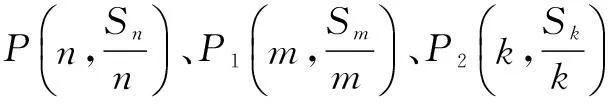
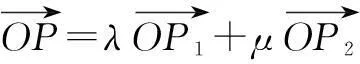
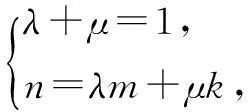
评注本题看似貌不惊人,但是它巧妙地把数列与平面向量整合在一块,运用三点共线得到解决,同时也体现了数形结合的数学思想方法.

四、以向量运算为先导结合面积之差得通项

(2)若四边形AnBnBn+1An+1的面积构成数列{an},求{an}(n∈N*)的通项公式.

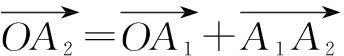
=j+(i+j)=i+2j=(1,2),

=2i+3j=(2,3),

=j+(n-1)(i+j)=(n-1,n),

∴An(n-1,n),它满足直线方程y=x+1,因此点An在直线y=x+1上.

设直线y=x+1交x轴于P(-1,0),则

an=S∆PAn+1Bn+1-S∆PAnBn

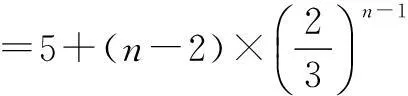
评注解决本题的关键是实现向量语言的转化,借助于向量和运算的坐标形式使问题得到解决.

本文通过例题揭示了平面向量与数列问题的融合,也体现了知识间的相互融合相互贯通,可见在高三的数学复习中应加强平面向量与立体几何、解析几何、三角函数等知识的综合应用.

(*)