巧用函数单调性解题
华瑞芬
(安徽省灵璧县黄湾中学,234213)
巧用函数单调性解题
华瑞芬
(安徽省灵璧县黄湾中学,234213)
函数是高中数学的重要内容,它不但是高考重点考察的热点之一,而且它的思想方法贯串于高中数学的始终.函数的单调性又是函数的一条非常重要的性质,它的应用十分广泛.在解题的过程中,若能深入地挖掘潜在条件,恰当地构造出相应的单调函数,巧妙地运用该性质,将会起到画龙点睛的作用,常常会收到出奇不意的效果,达到快速简捷求解的目的.下面举例说明函数的单调性在解题中的应用,目的在于使同学们对函数的单调性有更清醒的认识和更深刻的理解,并能够灵活地运用函数的单调性解决一些实际问题,以提高大家利用函数思想解题的能力.
一、比较大小
如果待比较的两个数或式子是同一个函数的函数值,常借助于函数的单调性来进行比较,有时需要先构造函数.
例1设f (x)=x2+bx+c对任意的实数t,都有f (2+t)=f (2 — t),试判断f (1)、f (2)、f (4)的大小.
解由f(2+t)=f(2-t) 知函数f(x)的图象关于直线x=2对称,且f (x)在[2,+∞)上是增函数,所以f(2) 则由不等式的传递性,知 对于某些待求代数式的值,可视为相应函数的一个特殊值,再利用该函数的单调性,把函数值的相等转化为自变量的相等,进而巧妙获解. 解由条件, (2y)3+sin(2y)+2a=0.设f(t)=t3+sin t,则f (x)=f (-2y)=2a,而f (t)在R上是增函数,所以x=-2y,x+2y=0,cos(x+2y)=1. 解令cos x=t,则 ∵0≤x≤π,∴-1≤t≤1. 而f (t) 在t∈[-1,1]上递增, ∴f(-1)≤f (t)≤f (1). 有些不等式是由抽象函数式组成的,通过单调性才能转化为自变量的不等式,进而求出不等式的解. 于是原不等式可化为log5(1+4t)>t,则 例6已知f (x)对任意的x,y∈R都满足条件f(x)+f(y)=2+f(x+y),且当x>0时,f(x)>2,f(3)=5.解不等式: f (a2-2a-2)<3. 解设x2>x1>0,则 x2-x1>0,故有f (x2-x1)>2. ∵f (x2)=f [(x2-x1)+x1] =f (x2-x1)+f (x1) -2>f(x1), ∴f (x)为单调增函数. ∵f (3)=f (2+1)=f (2)+f (1)-2 =[f (1)+f (1)-2]+f (1)-2 =3f (1)-4, 又∵f (3)=5,∴f (1)=3, ∴f (a2-2a-2) 故不等式的解为-1 设m>0,n>0,∵y=xα(α>0) 在 (0,+∞) 上单调递增, ∴am- bm与an-bn必同号,或同为0(当且仅当a=b时),从而 (am-bm) (an-bn)≥0 , 即am+n+bm+n≥ambn+anbm, 综上,得证. 评注原不等式等价于am+n+bm+n≥ambn+anbm⟺(am-bm) (an-bn)≥0,这可由幂函数y=xα(α>0) 在 (0,+∞) 上递增而得到. 该题可拓展:令m=sin2α,n=cos2α,则 a+b≥asin2αbcos2α+acos2αbsin2α. 例8设a,b>0,ab=ba,且a <1,试证:a=b. 证明取y=ax,当0 ∴ab>aa>ba,这与已知ab=ba相矛盾,故b 当0 ∴ab 这与已知ab=ba也相矛盾,故a 例9解方程3x+4x=5x. 例10已知函数f (x)=2x+lg(3x+1)的反函数为f-1(x),试判断方程f-1(x)=2实根的个数. 解容易看出f (x)是定义在 (-∞,+∞)上的增函数,则其反函数在它的定义域上也为单调增函数.由f (2)=5可知,f-1(x)=2有解x=5. 又据单调性可知,x=5是方程f-1(x)=2的唯一解,即该方程的实根个数为1个.

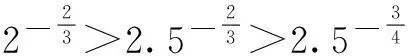
二、求值(值域)
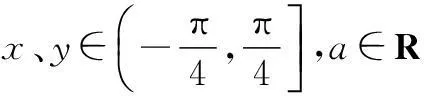

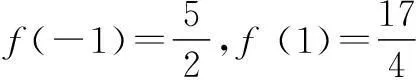

三、解不等式
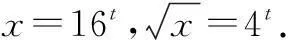


四、证明不等式(等式)
五、解方程

六、判断方程根的个数

