基于积分链式卡尔曼滤波器的角加速度观测器的噪声参数整定及性能研究

邱文彬　柴建云　陆海峰　曾颖宇　孙旭东

(电力系统及发电设备控制和仿真国家重点实验室(清华大学)　北京　100084)



基于积分链式卡尔曼滤波器的角加速度观测器的噪声参数整定及性能研究

邱文彬柴建云陆海峰曾颖宇孙旭东

(电力系统及发电设备控制和仿真国家重点实验室(清华大学)北京100084)

噪声统计特征值的整定是积分链式卡尔曼滤波器(IKF)的设计要点。针对噪声统计特征值的整定进行研究，推导出积分链式卡尔曼滤波器的离散噪声统计特征值与离散采样周期的函数关系，定量分析了积分链式卡尔曼滤波器的离散噪声统计特征值的跟踪性能。在此基础上，提出了一种定量计算噪声统计特征值的方法，通过滤波器截止频率、离散采样周期直接计算得到噪声统计特征值，改变了以往的仿真-实验-调整环整定方法，简化了设计流程。仿真和实验验证了所提出方法的有效性。

卡尔曼滤波器角加速度加速度观测器跟踪性能噪声统计特征值

0　引言

伺服控制系统是高端装备制造业的基础。通过加速度闭环控制、扰动转矩补偿控制、滑模变结构控制、自适应控制[1-13]等方式引入角加速度控制可有效提高系统的鲁棒性。如在工业机器人、数控机床等多轴机电系统的运行过程中，常伴随有参数变化和负载扰动，传统伺服系统受参数变化影响较大，系统的鲁棒性不足，而角加速度闭环可在不改变原控制系统的基础上，提高系统的鲁棒性，例如，基于加速度的负载扰动观测器在调速系统中得到了广泛研究和应用。

角加速度信号的获取主要有两种途径：一是通过角加速度传感器直接测量，二是通过位置信号间接观测。由于伺服电机大多已装配有高性能位置传感器，使得角加速度传感器的安装困难，另外，角加速度传感器会增加系统成本。所以，基于角位置测量的间接角加速度观测方法被认为是获取加速度信号的主要途径[14-21]。角加速度信号是位置信号的二阶差分值，直接差分运算会放大位置信号中的量化噪声，使观测精度受到严重影响。卡尔曼滤波器具有最优的白噪声抑制能力，但卡尔曼滤波器的设计在应用中一直存在两个难点：一是输入信号的白噪声模型，二是噪声的统计特征值。

文献[15-21]使用基于多项式曲线拟合和非线性反馈来构造角加速度观测器，该方法比直接差分法具有更好的噪声抑制能力，但非线性方法难以定量分析其噪声抑制性能。文献[22-25]提出了基于积分链式卡尔曼滤波器(All-Integrator Model Kalman Filter，IKF)的角加速度观测器，解决了用于观测角加速度的输入信号白噪声模型问题，文献在定性分析噪声参数特征值与观测性能的基础上，首先根据位置传感器的精度确定测量噪声的特征值，然后采用不断重复仿真-实验-调整的方法来整定输入信号噪声特征值，直到设计的观测器达到满意的噪声抑制性能。

本文对基于IKF的角加速度观测器进行了研究。首先，对基于连续IKF的角加速度观测器的噪声特征值与截止频率、稳态跟踪误差的关系进行研究；然后，定量分析了加速度观测器性能保持不变时，离散时间与离散IKF的噪声特征值的关系；在上述分析基础上，提出了整定IKF噪声特征值的方法，并对所提出方法进行仿真和实验，验证了方法的有效性。

1　基于IKF的加速度观测器

基于IKF的加速度观测器的状态方程为[23]

(1)

式中，输入噪声w(t)的统计特征值为qc；测量噪声v(t)的统计特征值为rc；加速度观测器的状态变量和系数矩阵分别为

(2)

由于将位置变量θ及其一阶、二阶微分作为状态变量，相邻状态变量之间存在积分关系，基于该状态方程的卡尔曼滤波器被称之为积分链式卡尔曼滤波器(IKF)。状态方程(1)的Riccati方程为

APc+PcAT-PcCT(rc)-1CPc+qcΓΓT=0

(3)

式中，Pc为状态变量x(t)的误差协方差矩阵。状态方程(1)以周期Ts离散化时，差分方程输入噪声w(k)的统计特征值为qd，测量噪声v(k)的统计特征值为rd，误差协方差矩阵的稳定值为Pd。若Ts足够小，差分方程式的Riccati方程可简化为[6]

(4)

2　基于IKF的噪声特征值设计

离期IKF在最优预测时，离散周期内加速度为常数，信号模型等效为二次多项式；在最优估计时，基于最小二乘的迭代运算将测量信号拟合为三次多项式曲线。

2.1基于IKF的加速度观测器的性质

2.1.1连续IKF的自由度与噪声特征值的关系

连续IKF只有qc/rc一个自由度，qc与rc同比变化时，卡尔曼滤波器的性能不变。由于卡尔曼滤波器与线性二次型最优控制系统存在对偶关系，状态方程(1)的卡尔曼滤波器反馈系数矩阵与线性二次型性能函数式(5)的最优反馈控制系数Kc相同。

(5)

若式(5)中线性二次型最优控制系统的控制系数Kc不变，则对偶的卡尔曼滤波器的反馈系数矩阵不变，所以卡尔曼滤波器的性能不变，连续IKF只有qc/rc一个自由度。

2.1.2连续IKF的截止频率与噪声特征值的关系

基于IKF的加速度观测器与三阶巴特沃斯滤波器的传递函数相同，截止频率ωc为

(6)

根据状态方程(1)及其Riccati方程式可得到观测角加速度x3的传递函数为

(7)

从式(7)可以看出，加速度x3的截止频率为qc/rc。例如卡尔曼滤波器状态方程的噪声特征值取值范围和离散周期Ts如表1所示时，首先，根据式(11)可得到离散卡尔曼滤波器的噪声特征值qd和rd；然后，将qd和rd代入卡尔曼滤波器进行循环迭代运算，得到稳定的系数矩阵Kd；最后，由反馈系数矩阵Kd得到加速度的离散传递函数，由离散传递函数可得到观测器的截止频率ωc。

表1　系统参数Tab.1　System parameters

对表1中的qc、rc进行遍历运算，图1为截止频率ωc与qc、rc的关系，图中离散周期与截止频率的乘积ωcTs最大值为0.314 2。

图1　加速度观测器的截止频率与qc、rc的关系Fig.1　The relationship between the cut-off frequency of the acceleration observer and the values of qc，rc

从图1中可看出，离散IKF只有qc/rc一个自由度，截止频率ωc与qc、rc的关系满足式(7)。

2.1.3连续IKF的稳态跟踪性能与噪声特征值的关系

根据式(7)可知，基于IKF的角加速度观测器对多项式位置信号的稳态观测误差为

(8)

输入位置信号为多项式时，观测角加速度x3的稳态观测误差如表2所示，位置信号为三次以下多项式

表2　加速度观测误差Tab.2　Error of the acceleration observed

时，观测加速度的稳态误差为零；位置信号为三次多项式时，观测加速度的稳态误差为直流偏置，与截止频率呈反比；位置信号为三次以上多项式时，观测加速度的稳态误差趋于无穷。

2.1.4离散IKF性能与离散化周期的关系

当CPdCT≪rd时，由差分方程及其简化的Riccati方程式可得到误差协方差矩阵稳态值Pd为

Pd=

(9)

差分方程的稳态反馈系数矩阵Kd为

(10)

连续IKF与离散IKF具有相同的性能，即误差协方差矩阵Pc和Pd相等时，对比式(3)和式(4)可知，连续噪声特征值与离散噪声特征值间存在如下关系

qd=qcTs

(11)

由式(11)可得

CPdCT+rd=rd(1+2ωcTs)

由于噪声特征值1/rd与截止频率的6次方呈正比，rd简化值使截止频率波动幅值小于0.1倍时，此时离散周期与截止频率存在如下关系

ωcTs≤0.45

(12)

当离散噪声特征值与连续噪声特征值满足式(11)时，离散化周期Ts越小，对卡尔曼滤波器的性能影响也越小。当离散周期与截止频率满足式(12)时，工程上可认为离散卡尔曼滤波器的性能与Ts无关。

通过例子说明此性质的意义。若卡尔曼滤波器状态方程的噪声特征值qc为600，rc为3×10-12时，截止频率fc为38.5 Hz。以Ts为1 ms时加速度观测器的幅频响应为基准值，截止频率与离散周期的乘积ωcTs为0.242，由式(7)和式(9)可得到差分方程的噪声特征值qd、rd以及反馈系数矩阵Kd，对应的加速度观测器幅频特性曲线如图2所示。当离散时间Ts取不同的值且满足式(9)时，加速度观测器幅频特性曲线的相对误差如图3所示，加速度观测器频率延时曲线如图4所示。

图2　Ts =1 ms时加速度观测器的幅频特性曲线Fig.2　Magnitude-frequency characteristic curve of the acceleration observer at Ts=1 ms

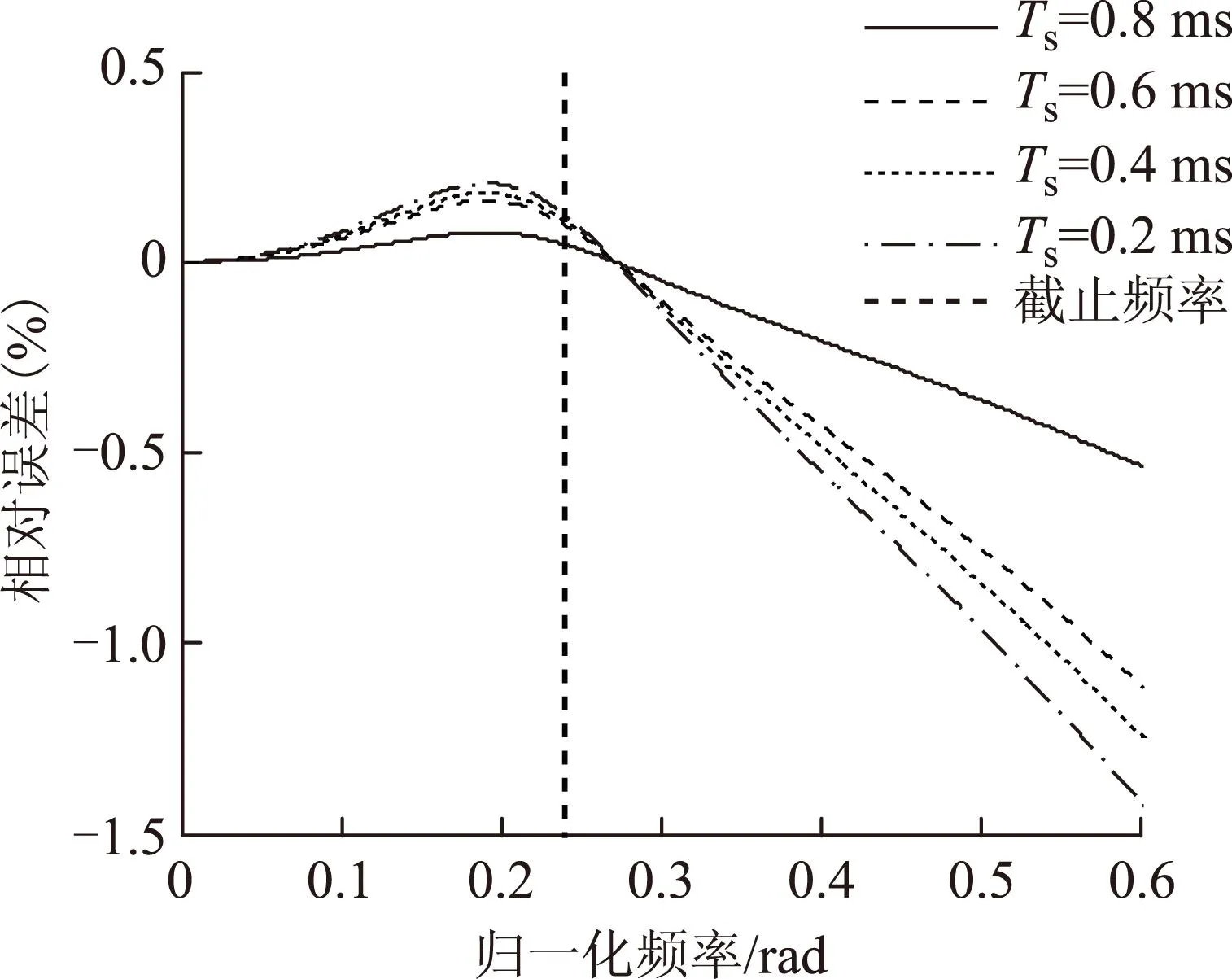
图3　不同离散时间下加速度观测器幅频特性曲线的相对误差Fig.3　The relative error of the Magnitude-frequency characteristic curves of the acceleration observer at different sampling periods

图4　不同离散时间下加速度观测器的延时-频率特性曲线Fig.4　The delay-frequency characteristic of the acceleration observer at different sampling periods

从图3和图4可看出，Ts取不同值时，加速度观测器的幅频特性曲线的相对误差在1.5%左右；频率延时曲线间的绝对误差约为0.4 ms，与基准频率延时特性曲线的相对误差在4%左右。以上分析可知，在离散频率与截止频率满足式(11)和式(12)约束时，Ts对离散卡尔曼滤波器性能的影响在设计要求内，即从工程实用的角度认为离散卡尔曼滤波器的性能与Ts无关。

2.2噪声特征值的整定步骤

传统积分链式卡尔曼滤波器的噪声特征值整定步骤为：

1)假设传感器测量噪声为均匀白噪声分布，求得测量参数噪声特征值rd。

2)任意给定qd初始值。

3)仿真和实验观测滤波器输出值，如果噪声过大，则执行步骤4，如果输出值的延时过长，则执行步骤5，如果符合要求，则停止整定进程。

4)减小qd，回到步骤3。

5)增大qd，回到步骤3。

基于IKF的加速度观测器的性质，本文提出一种根据截止频率来定量计算滤波器噪声特征值的方法，设计流程如图5所示，具体整定步骤如下：

1)由设计需求确定连续卡尔曼滤波器的截止频率ωc，选择离散周期Ts，使ωcTs的乘积满足式(12)。

2)连续卡尔曼滤波器的性能由qc/rc惟一决定，根据截止频率ωc与qc/rc满足式(7)，可求出qc/rc。

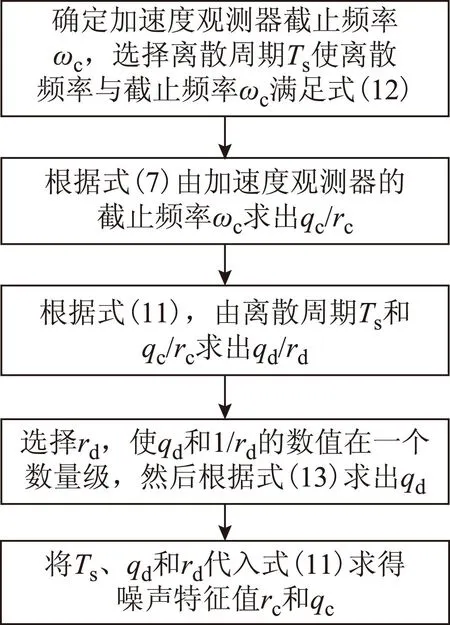
图5　噪声特征值整定流程Fig.5　Flow chart of the setting of the statistic characteristics of noises

3)将离散周期Ts和qc/rc代入式(11)，可计算得到qd/rd的值。

(13)

4)选择rd的值，使1/rd与qd在同一个数量级，然后求出qd的值。

(14)

5)将离散时间Ts、qd和rd代入式(11)得到连续卡尔曼滤波器的噪声特征值qc和rc。

3　仿真与实验验证

3.1仿真

根据本文所提出的方法，设计基于IKF的加速度观测器，使截止频率为45 Hz，计算过程如下：

根据截止频率fc为45 Hz，选择离散周期Ts为1 ms，截止频率与离散周期的乘积ωcTs为0.282 7，满足式(10)；将截止频率ωc代入式(12)，可求得qc/rc为5.11×1014；由qc/rc以及离散周期Ts可求得qd/rd为5.11×108；选取rd为2×10-5，此时，噪声特征值qd为1.022×104；将离散时间Ts、qd和rd代入式(7)可得到反馈系数矩阵稳定值Kd，此时，加速度观测器的离散传递函数为

上式的幅频特性曲线如图6所示，加速度观测器的截止频率为45 Hz，满足设计要求。

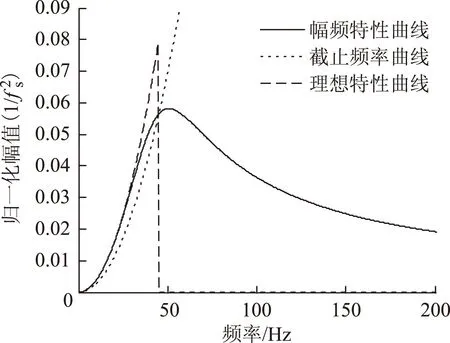
图6　幅频特性曲线Fig.6　Magnitude-frequency characteristic curve

当位置传感器为参数每周2000脉冲的光电编码器时，经过4倍频后编码器的分辨精度为0.27′，若输入10 Hz、幅值为11.5°的正弦波位置信号，基于IKF的角加速度观测器输出值如图7所示，位置信号直接二阶差分运算输出的观测加速度如图8所示。

图7　输入角加速度及卡尔曼滤波器观测的角加速度Fig.7　The input acceleration and the acceleration observed by the proposed Kalman filter

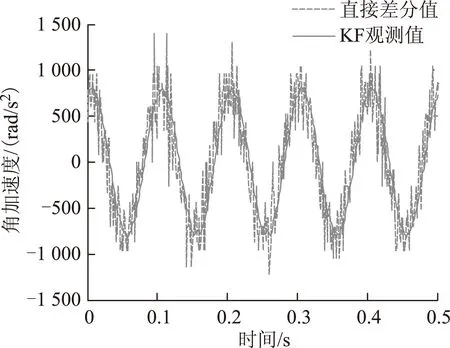
图8　直接二阶差分运算观测的角加速度Fig.8　The acceleration observed by the direct 2nd differential operation

图9　卡尔曼滤波器观测加速度及加速度误差Fig.9　The acceleration and the acceleration error observed by the proposed Kalman filter

从图7和图8可看出，当延时相近时，基于卡尔曼滤波器的加速度观测器相比直接差分运算拥有较好的噪声抑制能力。

实际输入加速度为±750 rad/s2的方波信号时，输入位置信号为二次多项式，角加速度观测值及观测误差如图9所示。从图中可看出，实际加速度出现阶跃变化时，观测加速度会在跃变瞬间出现误差，但很快就跟踪上实际加速度，且稳态输出误差为零，图中的噪声波动是由编码器的量化误差引起。

当参考加速度为三角波时，输入位置信号为三次多项式，加速度观测值及观测误差如图10所示。

图10　卡尔曼滤波器观测加速度及加速度误差Fig.10　The acceleration and the acceleration error observed by the proposed Kalman filter

从图10可看出，位置信号为三次多项式时，加速度观测器输出存在稳态误差，误差值与式(8)计算值相同。

仿真验证了本文所提的IKF的噪声特征值设计方法的正确性。当延时相近时，基于卡尔曼滤波器的加速度观测器相比直接差分运算拥有更好的噪声抑制能力；卡尔曼滤波器的加速度观测器的输出稳态误差与表3所示一致。

3.2实验

实验平台为类似PUMA工业机器人的第六臂，驱动器为松下伺服电机MSMD5AZS1，额定转矩为0.16 N·m，电机惯量为0.027×10-4kg·m2，负载率为1∶1时，额定加速度为2.963×104rad·s-2，输出轴连接有1∶100的谐波减速机，绝对位置编码器每周的编码数为217。

考虑到电机运行过程中的机械振动以及工频电源引入的干扰，设计加速度观测器的截止频率为20 Hz，离散周期Ts选择为0.5 ms，截止频率与离散周期的乘积ωcTs为0.062 8。根据本文所提的设计方法得到一组噪声特征值为

qd=qcTs≈5 907

当伺服电动机运行在恒定转速状态时，如图11所示，参考加速度为零，卡尔曼滤波器观测的加速度如图11b所示。

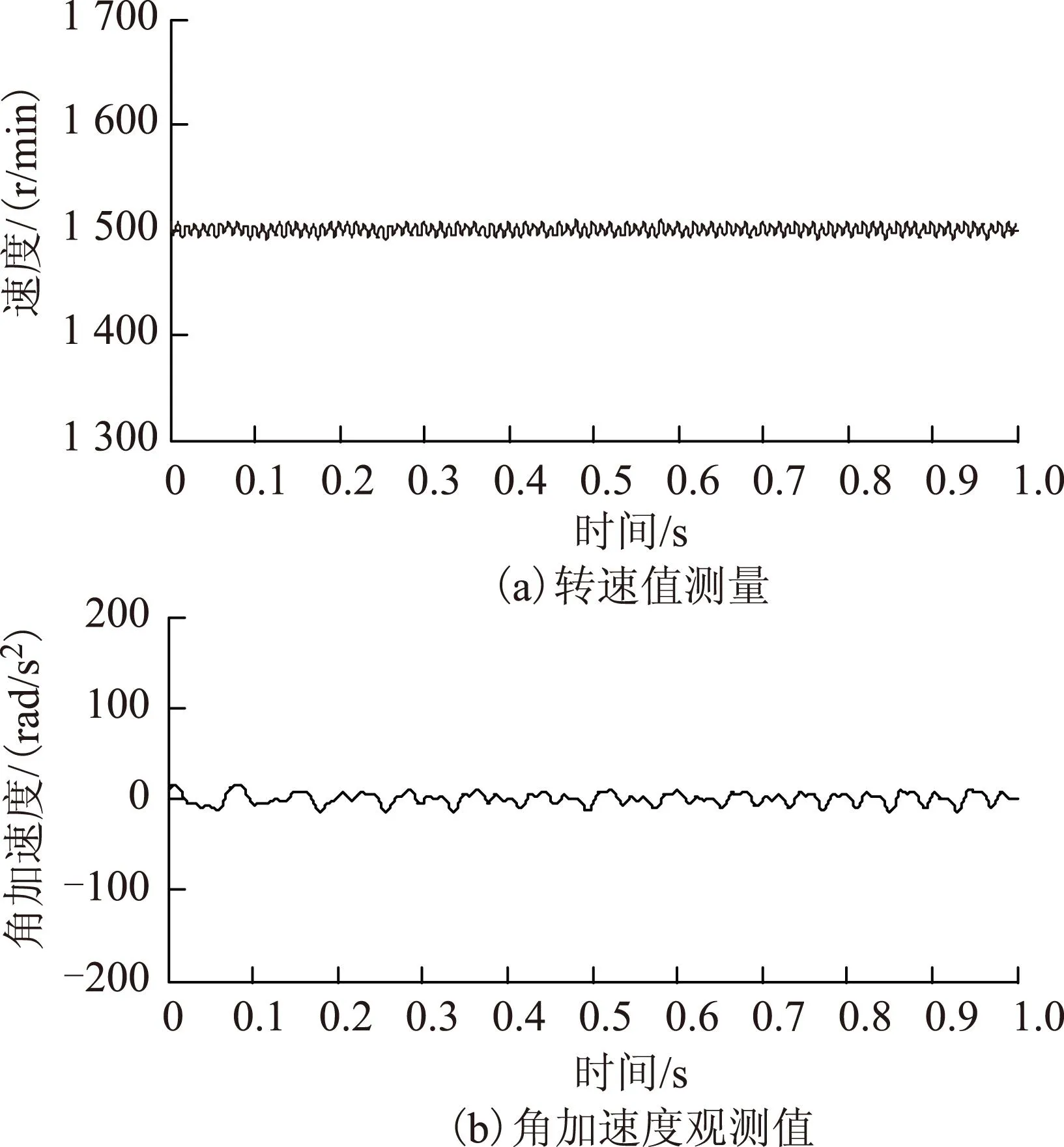
图11　恒转速条件下测量的转速及观测到的角加速度Fig.11　The measured speed and the observed acceleration at constant speed

从图11a可看出，速度的波动幅值为±5 r/min，相对误差在0.4%以内，说明速度的测量值中除了含有量化噪声外，还有其他周期噪声，观测加速度的输出如图11b所示，噪声引起的波动幅值为±15 rad/s2，相对额定值的绝对误差为0.05%。

当伺服电动机的转速呈梯形变化时，如图12a所示，卡尔曼滤波器观测的加速度如图12b所示。

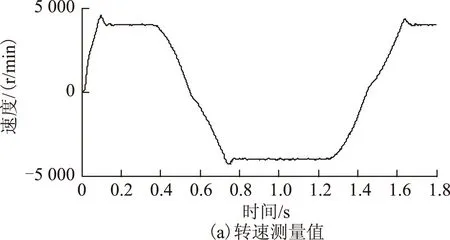
图12　变速条件下测量的转速及观测到的加速度Fig.12　The measured speed and the observed acceleration at varied speed

在图12b中，转速过零时，加速度存在幅值变小的阶跃，这是由于静摩擦力和减速器滞环的影响，图中，速度的波动幅值为±40 r/min，相对误差在1%以内，加速度观测值的波动幅值为±200 rad/s2，为加速度额定值的0.7%左右。

从图11和图12的速度波动幅值可看出，噪声特征值除了含有量化噪声外，还包括实际过程中引入的其他噪声，而从图中可看出，本文所提的噪声特征值设计方法，能一次性设计出符合要求的卡尔曼滤波器，而不需要像传统的设计方法一样，通过不断重复仿真-实验-调整流程来设计噪声特征值。

4　结论

本文针对基于IKF的角加速度观测器进行了研究。首先，由连续IKF的加速度观测器传递函数，得到了加速度观测器截止频率ωc与qc和rc的定量计算公式，在此基础上，分析了加速度观测器的ωc与稳态跟踪误差的关系；然后，通过对比简化后离散IKF和连续IKF的Riccati表达式，得到了截止频率ωc与qd和rd的关系以及截止频率ωc和离散时间Ts表示的离散IKF的Riccati表达式简化条件，获得了在不同离散时间Ts条件下，离散IKF的加速度观测器性能保持不变的关系；最后，在上述分析基础上，提出了一种根据截止频率定量设计噪声特征值的方法。

仿真分析和实验表明，本文所提的设计方法可一次性定量设计出指定性能的离散IKF噪声参数特征值，改变了以往通过不断重复仿真-实验-调整来设计噪声特征值的方法，克服了卡尔曼滤波器噪声特征值设计困难的问题，方便IKF角加速度观测器的广泛应用，同时也为研究基于IKF的速度观测器提供了新思路。

[1]Hori Y.Disturbance suppression on an acceleration control type DC servo system[C]//19th Annual IEEE Power Electronics Specialists Conference，Kyoto，Japan，1988，1：222-229

[2]Ohishi K，Matsuda S，Ohnishi K.DSP-based DC servo acceleration control without speed sensor[C]//Conference Record of the IEEE Industry Applications Society Annual Meeting，San Diego，CA，USA，1989，1：480- 485.

[3]Schmidt P B，Lorenz R D.Design principles and implementation of acceleration feedback to improve performance of DC drives[J].IEEE Transactions on Industry Applications，1992，28(3)：594-599.

[4]Xu W L，Han J D.Joint acceleration feedback control for robots：analysis，sensing and experiments[J].Robotics and Computer-Integrated Manufacturing，2000，16(5)：307-320.

[5]Dumetz E，Dieulot J Y，Barre P J，et al.Control of an industrial robot using acceleration feedback[J].Journal of Intelligent and Robotic Systems，2006，46(2)：111-128.

[6]Deur J，Peric N.A comparative study of servosystems with acceleration feedback[C]//Conference Record of the IEEE Industry Applications Conference，Rome，2000，3：1533-1540.

[7]于艾，杨耕，徐文立.具有扰动观测器调速系统的稳定性分析及转速环设计[J].清华大学学报(自然科学版).2005，45(4)：521-524.

Yu Ai，Yang Geng，Xu Wenli.Stability analysis and speed loop design of speed control system with disturbance observer[J].Journal of Tsinghua University(Science and Technology)，2005，45(4)：521-524.

[8]Katsura S，Irie K，Ohishi K.Wideband force control by position-acceleration integrated disturbance observer[J].IEEE Transactions on Industrial Electronics，2008，55(4)：1699-1706.

[9]Mitsantisuk C，Tran T P，Ohishi K，et al.Combining position and acceleration information for high performance of bilateral control using kalman-filter-based disturbance observer[C]//36th Annual Conference on IEEE Industrial Electronics Society，Glendale，AZ，2010：2069-2074.

[10]胡强晖，胡勤丰.全局滑模控制在永磁同步电机位置伺服中的应用[J].中国电机工程学报，2011，31(18)：61-66.

Hu Qianghui，Hu Qinfeng.Global sliding mode control for permanent magnet synchronous motor servo system[J].Proceedings of the CSEE，2011，31(18)：61-66.

[11]张晓光，孙力，赵克.基于负载转矩滑膜观测的永磁同步电机滑模控制[J].中国电机工程学服，2012，32(3)：111-116.

Zhang Xiaoguang，Sun Li，Zhao Ke.Sliding mode control of PMSM based on a novel load torque sliding mode observer[J].Proceedings of the CSEE，2012，32(3)：111-116.

[12]Corradini M L，Ippoliti G，Longhi S，et al.A quasi-sliding mode approach for robust control and speed estimation of PM synchronous motors[J].IEEE Transactions on Industrial Electronics，2012，59(2)：1096-1104.

[13]郑泽东，李永东，Maurice Fade，等.基于扩展Kalman滤波器的PMSM高性能控制系统[J].电工技术学报，2007，22(10)：18-23.

Zhen Zedong，Li Yongdong，Maurice Fadel，et al.High performance PMSM control system based on extended kalman filter[J].Transactions of China Electrotechnical Society，2007，22(10)：18-23.

[14]Ovaska S J，Valiviita S.Angular acceleration measurement：a review[J].IEEE Transactions on Instrumentation and Measurement，1998，47(5)：1211-1217.

[15]Lee S H，Song J B.Acceleration estimator for low-velocity and low-acceleration regions based on encoder position data[J].IEEE/ASME Transactions on Mechatronics，2001，6(1)：58-64.

[16]Lorenz R D，Pattern K W V.High-resolution velocity estimation for all-digital，AC servo drives[J].IEEE Transactions on Industrial Applications，1991，27(4)：701-705.

[17]纪科辉，沈建新.采用扰动转矩观测器的低速电机伺服系统[J].中国电机工程学报，2012，32(15)：100-106.

Ji Kehui，Shen Jianxin.A low speed servo motor drive system with disturbance torque observers[J].Proceedings of the CSEE，2012，32(15)：100-106.

[18]Väliviita S，Ovaska S J.Delayless recursive differentiator with efficient noise attenuation for control instrumentation[J].Signal Processing，1998，69(3)：267-280.

[19]Nagatomi H，Ohnishi K.Acceleration estimation method for motion control system with optical encoder[C]//IEEE International Conference on Industrial Technology，Mumbai，2006：1480-1485.

[20]Harrison A J，Mcmahon C A.Estimation of acceleration from data with quantization errors using control finite-difference methods[J].Proceedings of the Institution of Mechanical Engineers Part Ⅰ Journal of Systems & Control Engineering，1993，20(7)：77-86.

[21]Tian Dapeng，Shen Honghai，Dai Ming.Improving the rapidity of nonlinear tracking differentiator via feedforward[J].IEEE Transactions on Industrial Electronics，2014，61(7)：3736-3743.

[22]刘咔.角加速度控制系统研究[D].哈尔滨：哈尔滨工业大学，2008.

[23]Belanger P R，Dobrovolny P，Helmy A，et al.Estimation of angular velocity and acceleration from shaft-encoder measurements[J].The International Journal of Robotics Research，1998，17(11)：1225-1233.

[24]何玉庆，韩建达.基于卡尔曼滤波及牛顿预测的角加速度估计方法试验研究[J].机械工程学报，2006，24(2)：226-232.

He Yuqing，Han Jianda.Experimental study of angular acceleration estimation based on Kalman filter and Newton predictor[J].Chinese Journal of Mechanical Engineering，2006，24(2)：226-232.

[25]何玉庆，韩建达.一种新的角加速度估计方法及其应用[J].控制理论与应用，2007，24(1)：6-12.

He Yuqing，Han Jianda.A new angular acceleration estimation method and its application in acceleration feedback control[J].Control Theory and Applications，2007，24(1)：6-12.

[26]Ma Jie，Yao Yu.Angular acceleration estimator for a flight motion simulator：design and performance comparison[C]//17th Mediterranean Conference on Control and Automation，2009：606-609.

[27]Kalman R E.A new approach to linear filtering and prediction problems[J].Journal of Basic Engineering 1960，82(1)：35- 45.

[28]赵希梅，赵久威，李洪谊.基于GPC和DOB的直驱XY平台鲁棒跟踪控制[J].电工技术学报，2015，30(6)：150-154.

Zhao Ximei，Zhao Jiuwei，Li Hongyi.Robust tracking control for direct drive XY table based on GPC and DOB[J].Transactions of China Electrotechnical Society，2015，30(6)：150-154.

[29]陈松林，单梅林，王丽斌.基于干扰观测器的飞行仿真转台完全跟踪控制[J].电机与控制学报，2015，19(1)：113-118.

Chen Songlin，Shan Meilin，Wang Libin.Disturbance observer-based robust perfect tracking control for flight simulator[J].Electric Machines and Control，2015，19(1)：113-118.

[30]刘伯育.交流电机位置伺服系统的扰动补偿控制[J].机电工程，2014，31(1)：97-100.

Liu Boyu.Disturbance-rejection control of AC motor position servo systems[J].Journal of Mechanical and Electrical Engineering，2015，19(1)：113-118.

[31]郑泽东，李永东，肖曦，等.永磁同步电机负载转矩观测器[J].电工技术学报，2010，25(2)：30-36.

Zheng Zedong，Li Yongdong，Xiao Xi，et al.Load Torque observer of permanent magnet synchronous motor[J].Transactions of China Electrotechnical Society，2010，25(2)：30-36.

[32]郭鸿浩，周波，刘颖，等.永磁无刷直流电机角加速度估计[J].电工技术学报，2014，29(5)：93-103.

Guo Honghao，Zhou Bo，Liu Ying，et al.Angular acceleration estimation for a permanent magnet brushless DC motor[J].Transactions of China Electrotechnical Society，2014，29(5)：93-103.

[33]易伯瑜，康龙云，陶思念，等.基于两段卡尔曼滤波器的内置式永磁电机观测器设计[J].电工技术学报，2014，29(9)：110-118.

Yi Boyu，Kang Longyun，Tao Sinian，et al.Observer design of interior permanent magnet synchronous motors based on two-stage Kalman filter[J].Transactions of China Electrotechnical Society，2014，29(9)：110-118.

[34]刘艳莉，戴胜，程泽，等.基于有限差分扩展卡尔曼滤波的锂离子电池SOC估计[J].电工技术学报，2014，29(1)：110-118.

Liu Yanli，Dai Sheng，Cheng Ze，et al.Estimation of state of charge of lithium-ion battery based on finite difference extended Kalman filter[J].Transactions of China Electrotechnical Society，2014，29(1)：110-118.

Parameters Setting and Performance Research for the Angular Acceleration Observer Based on All-Integrator Model Kalman Filter

Qiu WenbinChai JianyunLu HaifengZeng YingyuSun Xudong

(State Key Laboratory of Control and Simulation of Power System and Generation Equipments Tsinghua UniversityBeijing100084China)

Obtaining the statistic characteristics of noises is the key point in the design of the all-integrator model Kalman filter (IKF).The setting of the statistic characteristics of noises has been studied in this paper.The function of the discrete statistic characteristics of noises and sampling period within the IKF has been derived.The tracking performance on the statistic characteristics of noises within the IKF has been quantitatively analyzed.On this basis，a method for calculating the statistic characteristics of noises by directly using roll-off frequency and discrete sampling period has been proposed，which overcomes the drawbacks of the traditional simulation-experiment-adjustment loop setting method and simplifies the design procedure.This proposed method is verified by simulations and experiments.

Kalman filter，angular acceleration，acceleration observer，tracking performance，statistic characteristics of noises

2015-04-28改稿日期2015-07-23

TM315

邱文彬男，1981年生，博士研究生，研究方向为伺服控制。

E-mail：qiuwb.hn@gmail.com(通信作者)

柴建云男，1961年生，教授，博士生导师，研究方向为风力发电、电机设计。

E-mail：chaijy@tsinghua.edu.cn