三相逆变电路的离线模型预测控制研究

韩建定　齐　蓉　雷晓犇　张东升

(1.西北工业大学自动化学院　西安　710129 2.空军工程大学航空航天工程学院　西安　710038)



三相逆变电路的离线模型预测控制研究

韩建定1齐蓉1雷晓犇2张东升2

(1.西北工业大学自动化学院西安710129 2.空军工程大学航空航天工程学院西安710038)

针对电力电子电路传统开关函数模型只描述电路的控制变迁而忽略了电路的条件变迁，可能导致电路动态信息丢失这一问题，建立了电力电子电路的混合逻辑动态模型，并将其作为预测模型。在此基础上，以电路可行解代替最优解，将可行解及移动闭塞的思想用于电路的模型预测控制(MPC)，可有效减少控制序列总数、降低开关频率，实现电路MPC的快速求解，克服了电路MPC的计算难题。详细研究了电力电子电路控制序列的求解算法及实现过程，并以三相逆变电路为例验证了控制方法的可行性与有效性。

模型预测控制混合逻辑动态建模逆变电路可行解移动闭塞

0　引言

模型预测控制(Model Predictive Control，MPC)是处理多变量系统和约束最优跟踪控制问题的有效方法之一[1]。近年来，已有大量文献对电力电子电路的MPC策略进行了研究。文献[2]通过建立DC-DC电路精确的混杂系统模型，设计了电路的受限MPC，使电压输出很好的跟踪电压给定，得到了良好的控制效果。文献[3]将5种不同方法用于DC-DC变换器的控制，通过分析MPC的现状，采用了一种离线优化、在线查表的MPC思路，有助于减少MPC的计算量。文献[4]从电压矢量的角度研究了两电平逆变电路的MPC，在每个采样时刻，通过优化目标函数选择最优电压矢量作为电路的控制信号。文献[5]建立了DC-DC电路的混杂系统预测模型和基于最小开关损耗的目标函数，研究了电路最小开关损耗的MPC策略。

目前电力电子电路MPC主要面临的难题是：由于电路逻辑变量的影响及求解混合整数线性规划问题的复杂性，在极短的采样时间内(一般为几十微秒)在线求解电路控制具有很大难度[6]。

本文建立了电力电子电路的混合逻辑动态模型(Mixed Logic Dynamic Model，MLD)，并将其作为MPC的预测模型，应用基于可行解及移动闭塞策略的MPC方法，以两电平逆变电路[7]为例，新的控制策略具有以下特征[8]：

1)运用了可行解的思想，以可行解代替最优解，不仅可降低开关频率，减少电路损耗，而且避免了寻找最优解的复杂计算过程，防止特殊条件下由于最优解不存在而导致电路出现不可控的情况。

2)引入移动闭塞策略，使功率管仅在电路采样时刻动作而忽略预测时域内功率管的动作，从而将电路控制序列总数从8N减少至8(N为预测时域)，降低了电路MPC的求解难度。

3)将电路k时刻的控制序列作为k-1时刻控制序列和k时刻电路状态的函数，离线预先求解电路k时刻的可行解，将求解结果以表格储存，电路工作时以查表形式在线实时得到电路的控制序列，从而克服了MPC需要在线求解混合整数线性规划问题的难题。

1　电力电子电路的混合逻辑动态模型

混杂系统是指由连续变量动态系统和离散事件动态系统相互混杂、相互作用的系统，因其具有良好的建模特性成为近年来研究的热点[9]。电力电子电路是一种典型的混杂系统[10]，可以利用混杂系统理论和方法分析研究电力电子电路精确的数学建模与控制方法。

MLD作为混杂系统建模方法中的一种，是将系统整个当作一个微分方程组来处理，离散事件以条件的方式嵌入微分方程组中。与电力电子电路传统开关函数模型[11]相比，MLD兼顾了电路的控制变迁和条件变迁，能更好的反映电路的特性[12]。

准确的数学模型是实现精确控制的基础，建立电力电子电路混合逻辑动态模型，并将其作为电路MPC的预测模型可提高控制的性能。

根据MLD理论，可以建立电力电子电路的混合逻辑动态模型为

x(k+1)=Ax(k)+B1u(k)+B2σ(k)+B3z(k)

y(k)=Cx(k)+D1u(k)+D2σ(k)+D3z(k)

E2σ(k)+E3z(k)≤E1u(k)+E4x(k)+E5

(1)

式中，x为状态变量，x=(xc，xl)T，其中连续状态xc∈Rnc， 离散状态xl∈(0，1)nl，n=nc+nl；y为输出变量，y=(yc，yl)T，其中连续输出yc∈Rpc， 离散输出yl∈(0，1)pl，p=pc+pl；u为输入变量，u=(uc，ul)T，其中连续输入uc∈Rmc， 离散输入ul∈(0，1)ml；σ和z分别为系统辅助逻辑变量和辅助连续变量。

2　电力电子电路基于可行解及移动闭塞策略的模型预测控制

2.1基本概念

有关MPC理论可参考文献[13]，本文不再详述。为了便于后文说明，首先给出有关可行解的两个定义：

定义1：能使被控变量Y=(y1，…，yi，…，ym)保持在设定界限以内的控制序列ui称为电路的可行解，可见电路的可行解并不惟一。

定义2：电路所有可行解组成的集合U={u1，…，ui，…，un}称为电路的可行解集。

电力电子电路的工作点给定，预测时域为N，设定被控变量Y的上、下界限Ymax及Ymin，建立预测模型如式(1)所示，电路控制的目标是寻找满足以下两个条件的控制序列：

1)必须是电路可行解，但不一定是最优解。

2)可行解集中使电路开关频率最小的解。

引入可行解的思想，以可行解代替最优解，可明显降低开关频率，减少电路损耗，避免寻找最优解的复杂计算[14]。

另外，如果每一步预测功率管都动作，电力电子电路的控制序列数目将非常巨大(如两电平逆变电路是8N，而三电平逆变电路则为27N)，从而较难或无法实现电路的MPC，因为电路需要在极短的采样时间内(一般为几十微秒)从所有的控制序列中选择能使开关频率最小的可行解。为此，本文引入移动闭塞的思想，使功率管仅在电路采样时刻动作而忽略预测时域内功率管的动作，从而将两电平逆变器的控制序列总数从8N减少至8，三电平逆变器的控制序列总数从27N减少至27，可极大的降低电路MPC的求解难度。

2.2求解算法及控制原理

本节对电力电子电路控制序列的求解算法及其MPC的具体实现进行详细介绍。为便于说明，首先给出如下定义，其中n为预测步数，n≤N。

k时刻电路状态向量为x(k)，X0为电路的状态向量空间，若

u(k)=u(k-1)

(2)

(3)

同时，将满足式(4)的电路状态向量集合称为电路的环。

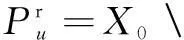
(4)

(5)

(6)

在以上电路求解算法的基础上，可得到电路控制的基本原理如图2所示，将k时刻电路的控制u(k)作为u(k-1)及状态变量x(k)的函数，应用图1算法预先计算电路的控制序列，将结果存于表格。电路工作时，通过实时观测电路k-1时刻的控制序列u(k-1)及k时刻电路的状态变量x(k)，经查表得到电路的控制u(k)。

图1　算法流程Fig.1　Flow chart of algorithm

图2　控制原理Fig.2　Diagram of control principle

3　逆变电路的模型预测控制

与DC-DC电路相比，两电平逆变电路[15]的被控变量是交变的，因而逆变电路的控制更为复杂，但更易于推广应用于其他电路[16]。因而本节以两电平逆变电路为例，如图3所示，通过MLD建立逆变电路的预测模型，按照图1所示控制序列求解算法及图3控制原理，设计逆变电路的控制器，验证以上控制方法的正确性及有效性。

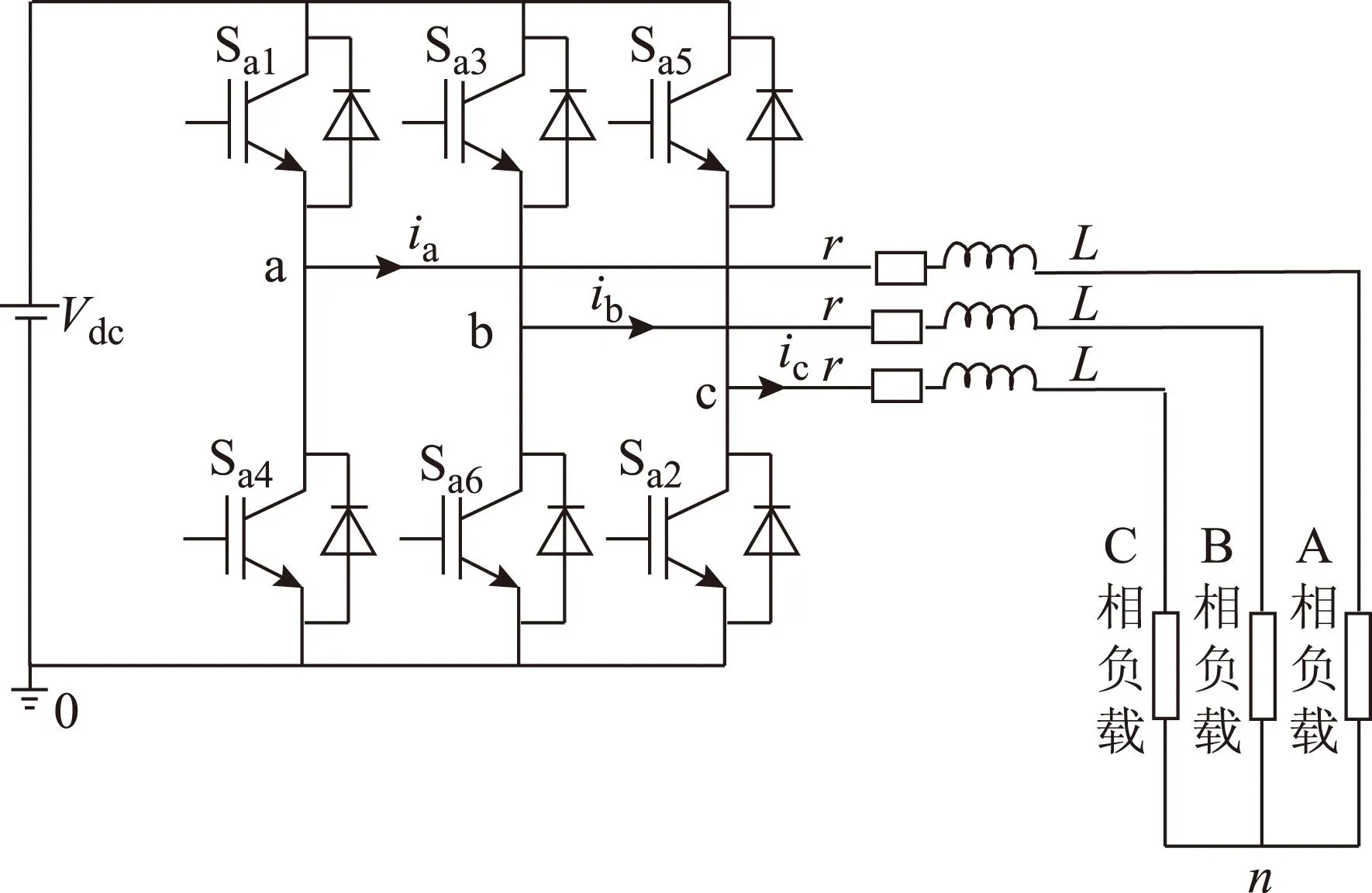
图3　三相逆变电路Fig.3　Three-phase inverter diagram

取功率管Sa1～Sa6的控制信号为s1～s6(“1”表示导通，“0”表示关断)，对于逆变电路a臂(b、c两臂类似)，定义电流ia流入滤波电感的方向为正，引入逻辑运算符[17，18]：“∨”表示析取、“Λ”表示合取、“～”表示取非、“↔”表示等价，引入逻辑变量如式(7)所示，将离散事件ia>0和ia<0分别用逻辑变量σa=1和σa=0表示，则有

(7)

对于三相逆变电路，根据其工作原理，可得到如下逻辑关系式

[s1=0， s4=1， σa=1]∨[s1=0， s4=0， σa=1]

∨[s1=0， s4=1， σa=0]↔[uao=0]

[s1=1， s4=0， σa=1]∨[s1=0， s4=0， σa=0]

∨[s1=1， s4=0， σa=0]↔[uao=Vdc]

(8)

由上述逻辑关系得到电压uao的数学描述为

(9)

式中，ua0表示a相输出端a与接地点0之间的电压。

假定电路滤波电阻值均为r，电感值为L，负载电阻值为R，uA、uB、uC分别为三相输出电压，得到逆变器的MLD向量模型为

y=Cx

(10)

式中

由式(10)可见，与电路传统开关函数模型相比，混合逻辑动态模型包含9个逻辑变量，分别是表示离散事件的逻辑变量δa、δb和δc以及功率管Sa1～Sa 6的控制信号s1～s6，因此混合逻辑动态模型具有更大的灵活性，为精确描述实际系统提供了方便，有助于实现电路高性能的控制。

将式(10)离散化

x(k+1)=A*x(k)+B*u(k)

y(k)=Cx(k)

(11)

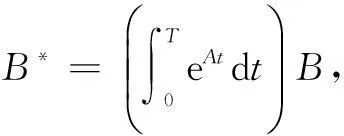
对于逆变电路a臂，引入开关函数sa如式(12)所示，以同样方式定义b、c两臂的开关函数sb、sc，从而电路的控制序列可表示为U=(sa，sb，sc)，共有8种不同的控制序列。引入的开关函数与功率管Sa1～Sa6的控制信号s1～s6间的关系如式(13)所示。

(12)

(13)

设定电路预测时域为N，被控输出变量的界限如式(14)所示，其中yref为电路参考输出，m为设定的允许带宽，采样周期为T，滤波电感的最大允许电流为imax，从而不等式组(15)构成了电路的状态空间X0，电流值为负时表示电流反向。

(14)

(15)

(16)

(17)

(18)

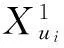
(19)

(20)

(21)

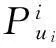
4　仿真与实验验证

如图3所示逆变器拓扑，基于Matlab搭建其仿真模型，仿真参数为：Vdc=270 V，滤波电感L=550 mH，滤波电阻R=25 mΩ，额定频率为400 Hz，采样周期T=25 μs，预测时域N=1。图4为电路的混合逻辑动态模型和传统开关函数模型的跟踪误差，可见混合逻辑动态模型能更精确的反映电路的特性。

图4　MLD与开关函数建模及其误差Fig.4　Diagram for MLD，switch function and error

将详细的电路状态变量集合信息存入表格，如图2所示，设计电路控制器，利用电路前一时刻控制序列信息、当前时刻状态信息及时间信息实时查表，得到电路当前时刻最佳控制序列，完成对电路输出电压的控制。图5为电路a相输出电压信号，与图6传统PID控制相比，在同一时段的250 μs内，MPC使电路开关频率得到了明显降低。

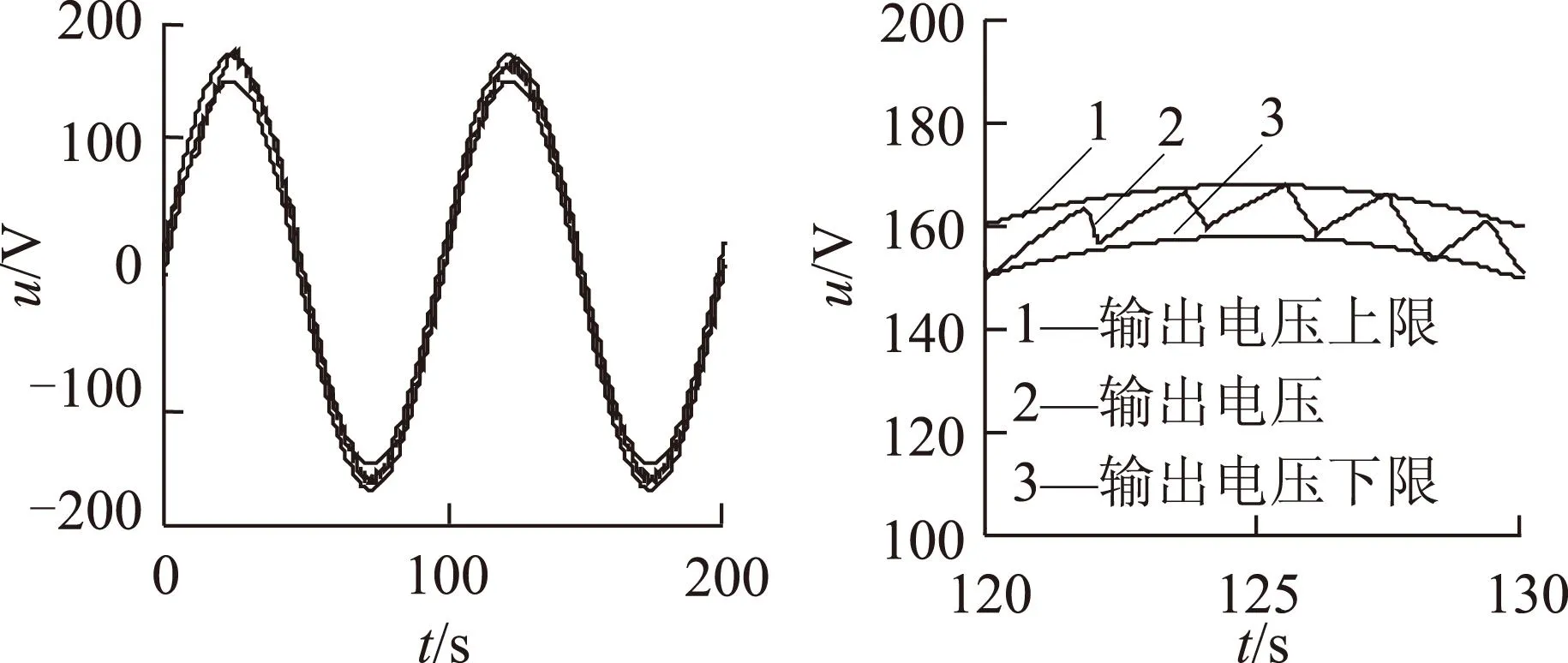
图5　电路MPC输出电压及开关频率Fig.5　Diagram for voltage and switch frequency of MPC

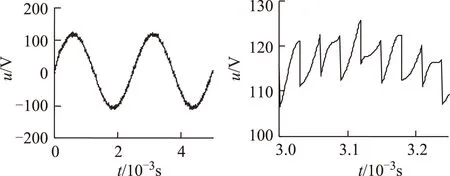
图6　电路PID控制输出电压及开关频率Fig.6　Diagram for voltage and switch frequency of PID

实验平台基于TMS320C6713，利用IRF620 MOSFET和RURP1560 二极管搭建电路。实验结果如图7和图8所示，图7为电路的三相输出电压波形，可以看出，输出电压波形具有较大的纹波，这是由于电路功率开关管只在输出电压值超出允许带宽时动作，与传统控制方法相比，开关频率较低造成的。通过对输出电压进行傅里叶分析，基波幅值为154.5 V，而总谐波含量为3.34%，能够满足航空领域对中频逆变电路的要求。图8为电路由空载到满载的实验波形，可以看出，满载后电路具有较大的纹波，因为开关频率较低，满载后电压基波幅值为153.7 V，而总谐波含量为4.09%，满足航空要求，可见控制策略暂态性能良好。

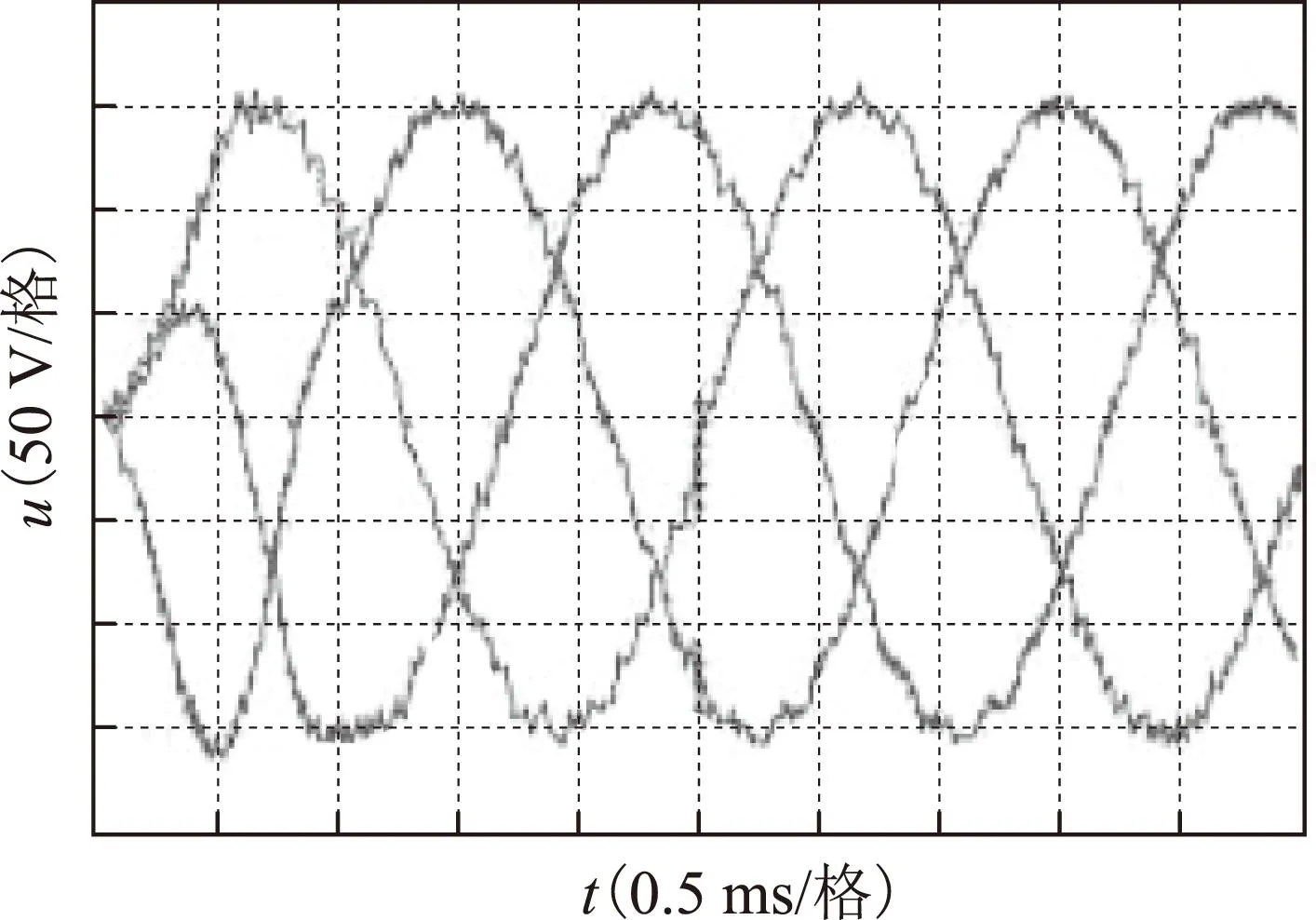
图7　电路输出电压波形Fig.7　Diagram for output voltage

图8　空载-满载时电路输出电压波形Fig.8　Diagram for output voltage from no-load to full-load

5　结论

本文针对电力电子电路MPC的计算难题，应用了可行解及移动闭塞的思路，通过电路MLD，研究了电力电子电路MPC的求解算法及控制原理，以两电平逆变电路为例，验证了所提方法的正确性和有效性，与传统控制方法相比，新的控制方法在保证控制性能的同时使电路具有较小的开关频率，为其他电力电子电路的控制提供了参考。

[1]郑雪生，李春文，戎袁杰.DC/AC变换器的混杂系统建模及预测控制[J].电工技术学报，2009，24(7)：87-92.

Zheng Xuesheng，Li Chunwen，Rong Yuanjie.Hybrid dynamic modeling and model predictive control for DC/AC converter[J].Transactions of China Electrotechnical Society，2009，24(7)：87-92.

[2]Geyer T，Papafotiou G，Frasca R，et al.Constrained optimal control of the step-down DC-DC converter[J].IEEE Transactions on Power Electronics，2008，23(5)：2454-2464.

[3]Mariethoz S，Almer S，Baja M，et al.Comparison of Hybrid control techniques for buck and boost DC-DC converters[J].IEEE Transactions on Control Systems Technology，2010，18(5)：1126-1142.

[4]Cortes P，Ortiz G，Yuz J I，et al.Model predictive control of an inverter with output LC filter for UPS applications[J].IEEE Transactions on Industrial Electronics，2009，56(6)：1875-1883.

[5]Fischer C，Mariethoz S，Morari M.Multisampled hybrid model predictive control for pulse-width modulated systems[C]//50th IEEE Conference on Decision and Control and European Control Conference，Orlando，FL，2011：3074-3079.

[6]Papafotiou G，Geyer T，Morari M.A hybrid model predictive control approach to the direct torque control problem of induction motors[J].International Journal of Robust and Nonlinear Control，2007，17(7)：1572-1589.

[7]刘苗，洪峰，尹培培，等.复合型级联双Buck飞跨电容五电平逆变器[J].电工技术学报，2015，30(18)：35- 42.

Liu Miao，Hong Feng，Yin Peipei，et al.A hybrid cascaded dual Buck flying-capacitor five-kevel inverter[J].Transactions of China Electrotechnical Society，2015，30(18)：35- 42.

[8]魏永清，贺慧英，向东，等.交流传动系统的混合型逆变器控制技术研究[J].电工技术学报，2015，30(14)：320-324.

Wei Yongqing，He Huiying，Xiang Dong，et al.Control technology of hybrid inverters for AC drive system[J].Transactions of China Electrotechnical Society，2015，30(14)：320-324.

[9]李宁，李颖晖，朱喜华，等.混杂系统理论及其在三相逆变电路开路故障诊断中的应用[J].电工技术学报，2014，29(6)：114-119.

Li Ning，Li Yinghui，Zhu Xihua，et al.Fault diagnosis for power electronic circuits based on mixed logic dynamic model and incident identification vector[J].Transactions of China Electrotechnical Society，2014，29(6)：114-119.

[10]袁佳歆，薛钢，赵震，等.三相逆变器无死区最优矢量控制研究[J].电力系统保护与控制，2014，42(24)：18-24.

Yuan Jiaxin，Xue Gang，Zhao Zhen，et al.New optimal dead-time elimination for three-phase voltage source inverters[J].Power System Protection and Control，2014，42(24)：18-24.

[11]王晓刚，张杰.基于开关电感的增强型Z源三电平逆变器[J].电力系统保护与控制，2015，43(16)：65-72.

Wang Xiaogang，Zhang Jie.Enhanced Z-source three-level inverter based on switched-inductor[J].Power System Protection and Control，2015，43(16)：65-72.

[12]张志学，马皓，毛兴云.基于混杂系统模型和事件辨识的电力电子电路故障诊断[J].中国电机工程学报，2005，25(3)：49-53.

Zhang Zhixue，Ma Hao，Mao Xingyun.Fault diagnosis for power electronic circuits based on hybrid system theory and event identification[J].Proceedings of the CSEE，2005，25(3)：49-53.

[13]李宁，李颖晖，朱喜华，等.新型逆变器的混杂系统建模与故障诊断[J].电机与控制学报，2012，16(9)：51-58.

Li Ning，Li Yinghui，Zhu Xihua，et al.Hybrid system modeling and fault diagnosis of fault tolerant inverter [J].Electric Machines and Control，2012，16(9)：51-58.

[14]方辉，宋文胜，冯晓云，等.三电平SVPWM与CBPWM算法的内在联系研究[J].电工技术学报，2014，29(10)：19-26.

Fang Hui，Song Wensheng，Feng Xiaoyun，et al.Relationship between three-level SVPWM and CBPWM[J].Transactions of China Electrotechnical Society，2014，29(10)：19-26.

[15]李素非，李国杰，翟登辉，等.级联型多电平逆变器最小总谐波失真阶梯调制策略研究[J].电力系统保护与控制，2014，42(19)：8-17.

Li Sufei，Li Guojie，Zhai Denghui，et al.Staircase modulation strategy with minimum total harmonic distortion for cascaded multilevel inverters[J].Power System Protection and Control，2014，42(19)：8-17.

[16]Geyer T，Papafotiou G.Direct torque control for induction motor drives：a model predictive control approach based on feasibility[J].Hybrid Systems：Computation and Control，2005，274-290.

[17]李宁，李颖晖，韩建定，等.基于混合逻辑动态模型的三相逆变电路有限控制集模型预测控制策略[J].电网技术，2014，38(2)：375-380.

Li Ning，Li Yinghui，Han Jianding，et al.FCS-MPC strategy for inverters based on MLD model[J].Power System Technology，2014，38(2)：375-380.

[18]王萌，施艳艳，沈明辉，等.三相电压型整流器模型电压预测控制[J].电工技术学报，2015，30(16)：49-55.

Wang Meng，Shi Yanyan，Shen Minghui，et al.Model voltage predictive control for three-phase voltage source rectifier[J].Transactions of China Electrotechnical Society，2015，30(16)：49-55.

The Off-Line Model Predictive Control for Three-Phase Inverter

Han Jianding1Qi Rong1Lei Xiaoben2Zhang Dongsheng2

(1.School of AutomationNorthwestern Polytechnical UniversityXi’an710129China 2.Aeronautics and Astronautics Engineering CollegeAir Force Engineering UniversityXi’an710038China)

Traditional switch function model for power electronics circuits only describes the control changes of circuits rather than their conditional changes，which may cause a loss of their dynamic information.Considering this fact，this paper establishes a mixed logic dynamic (MLD) model for power electronic circuits as a predictive model.Based on it，the optimal solution will be replaced by the feasibility solution which，together with the move blocking principle，will be applied to the circuit model predictive control (MPC) so as to effectively reduce the total number of control sequence and the switch frequency，and realize the fast solution of circuits，which offers a solution to the hard problem of calculating circuit MPC.The paper elaborates the algorithm and realization procedure of the control sequence of power electronic circuits and verifies the feasibility and validity of the algorithm by the three-phase inverter circuit.

Model predictive control，mixed logic dynamic model，inverter，feasibility，move blocking

2015-04-19改稿日期2015-10-29

TM46

韩建定男，1971年生，博士研究生，研究方向为新型电能变换技术。

E-mail：hanjiandinghjd@sina.com(通信作者)

齐蓉女，1962年生，教授，博士生导师，研究方向为现代电力电子与电力传动技术。

E-mail：lhqr@nwpu.edu.cn

国家自然科学基金(61074007)和陕西省自然科学基金(2012JM8016)资助项目。