某低矮模型房屋实测风场和风压的相关性研究*1

李正农，余　蜜，吴红华，史文海

(1.湖南大学 建筑安全与节能教育部重点试验室，湖南 长沙　410082;2.温州大学 建筑工程学院，浙江 温州　325035)



某低矮模型房屋实测风场和风压的相关性研究*1

李正农1†，余蜜1，吴红华1，史文海2

(1.湖南大学 建筑安全与节能教育部重点试验室，湖南 长沙410082;2.温州大学 建筑工程学院，浙江 温州325035)

基于台风“菲特”影响下温州某低矮房屋的环境风场实测数据及该建筑物屋盖上的风压实测数据，对于风场特性和屋盖风压特性参数进行了计算分析.分析结果表明：随着平均时距的减小，平均风速最大值增大；湍流度随着平均风速的增大呈逐渐减小的趋势；建筑物屋面及屋面屋脊边缘处的平均风压均为较大的负压且脉动较大；根据风速和风压的变化趋势可以看出，风场风速与建筑物屋盖上风压呈现明显的相关性，进而在不同的时距条件下对风场风速与屋盖风压的相关性进行了分析，发现取5min为基本时距时风速与风压的相关性系数值较高，说明在确定结构的风荷载时取基本时距为5min更为合理.

低矮房屋；风场；风压；相关性

通过研究各国的建筑设计规范可知[1-2],在计算结构的风荷载时首先需要确定的是结构可能遭遇的最大平均风速，而平均风速是根据在一定的时间段内实测得到的多个瞬时风速测量值通过平均计算得出的.各国建筑设计规范所规定的计算平均风速时所确定时间段的长度(即基本时距)是不尽相同的,国际上许多国家( 包括中国) 将平均风速计算时距值取为 10min(即在10min实测获得多个瞬时风速值，然后计算平均风速值，但也有国家取为1h( 如加拿大等) ,甚至有的国家取为3～5s时距的瞬时风速( 如美国规范取为3s) .显然在风荷载计算时，取不同的时距得到的平均风速结果是不同的.对于高层建筑而言, 究竟时距长度取何值时最为适宜, 已有学者进行了分析[3]，但对于低矮建筑是否有相同规律尚无定论[4-8].本文主要通过对一幢足尺低矮房屋模型实验房在台风“菲特”影响温州期间，对登陆时的风场及其屋盖迎、背风面风压的实测数据进行了相关性分析, 研究了在不同时距条件下对风场和风压的相关性大小的影响, 从而确定在低矮建筑风荷载计算时最为合理的基本时距.

1　实验房概况

本课题组于2012年4月经过精心设计与选址，在温州滨海园区建造了一幢足尺低矮实验房用于抗风研究.实验房所在地为海涂围垦地形，平坦、开阔，东南面距离东海约1.3km，实验房地理位置如图1所示.该实验房为一幢两层板房，主体受力结构为钢骨架，基础为整体现浇钢筋混凝土.实验房总高6.7m，长7.6m，宽4.95m，为前后对称的双坡屋顶(屋面角为20°)，屋面开洞30个，用于安装屋面风压传感器，其布置详图如图2所示.在实验房东北面6m处架设了一座可自由升降的10m高测风塔，分别在3.5m，6.8m和10m塔高处安装了3台R.M.YOUNG05103V型螺旋桨式风速、风向传感器进行观测风场，采用优泰32通道动态数据采集分析系统对风场数据进行同步采集，采样频率为25.6Hz.实测足尺模型实验房及测风塔整体图如图3所示.

2　风场特性分析

2.1平均风速和风向

在2013年第23号台风“菲特”(Fitow)登陆期间开展了实测研究,获得了大量的风场实测数据.本文在具体分析时选取了地面以上10m高度处10月6日17:45～19:25时间段内的风场(风速风向)数据进行了分析.

图2　风压传感器布置Fig.2　The arrangement of wind pressure sensors

图3　实验房及测风塔整体图Fig.3　Instrumented building and anemometer tower

在实测时，将风向角定义正北风为θ=0°，正南风为θ=180°，角度按顺时针递增，风速则可以根据式(1),(2)分解为两个分量：

ux(t)=u(5)cosθ(t)，

(1)

uy(t)=u(t)sinθ(t)．

(2)

式中：ux为南北向分量；uy为东西向分量.在具体计算分析时若取t为基本时距，则主风速u和主风向φ为：

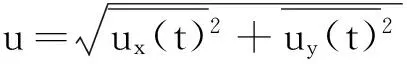
(3)

(4)

式中：

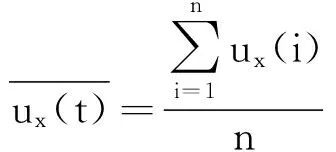
(5)

(6)

表示t时距样本的二维风速平均值.式中n为t时距段内的采样个数.

分别以10min，5min，30s和10s为基本时距，测得的水平向平均风速和风向数据分别如图4(a)和4(b)所示，时间段长度为100min.从图4看出，以10min为基本时距所测得的平均风速为7～12m/s，平均风向位于10°～35°之间.对于其他的时间间距，取相对应的数值进行计算，即可得到对应于时间间距的平均风速和风向.

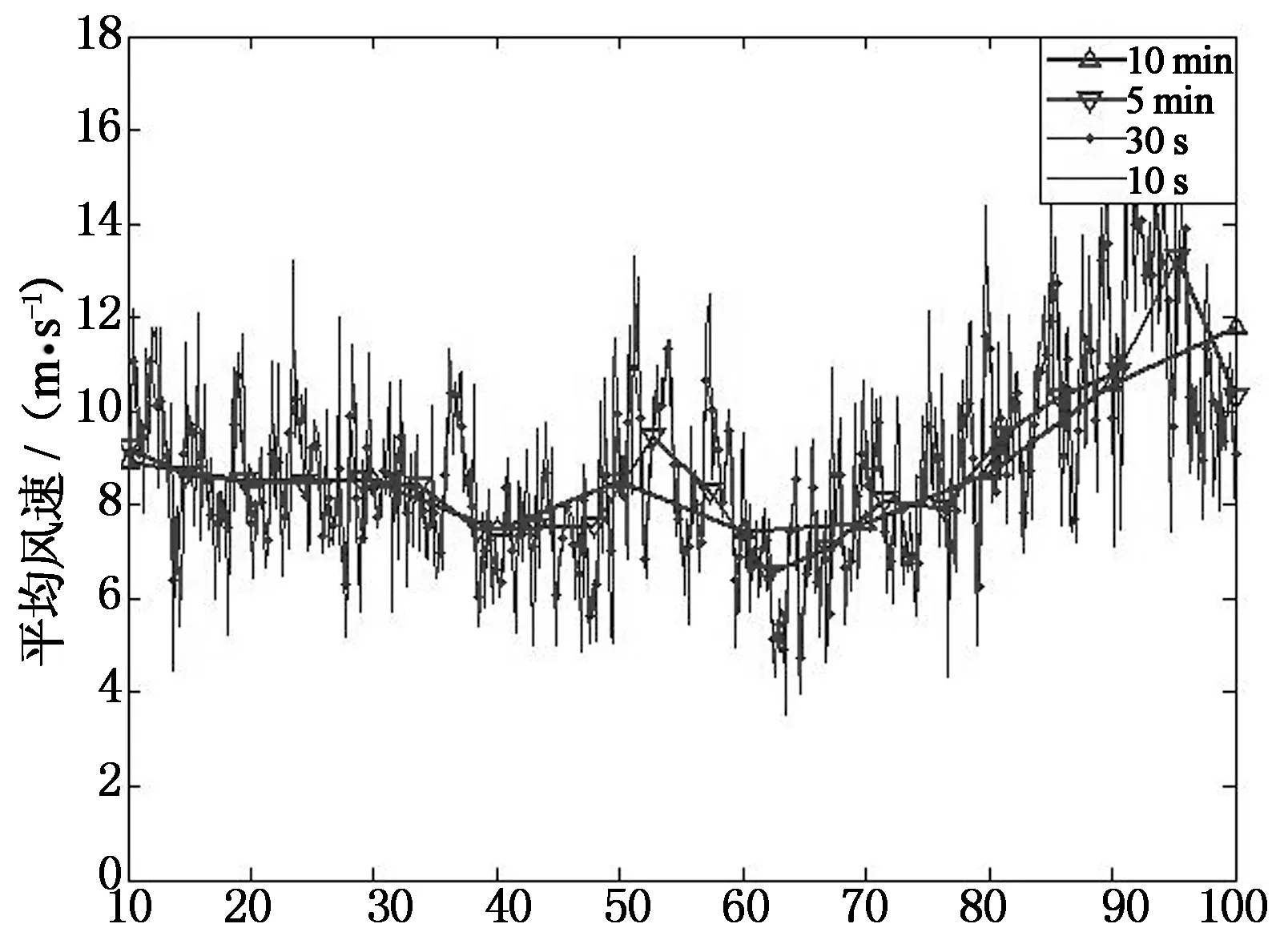
t/min(a)平均风速变化历程

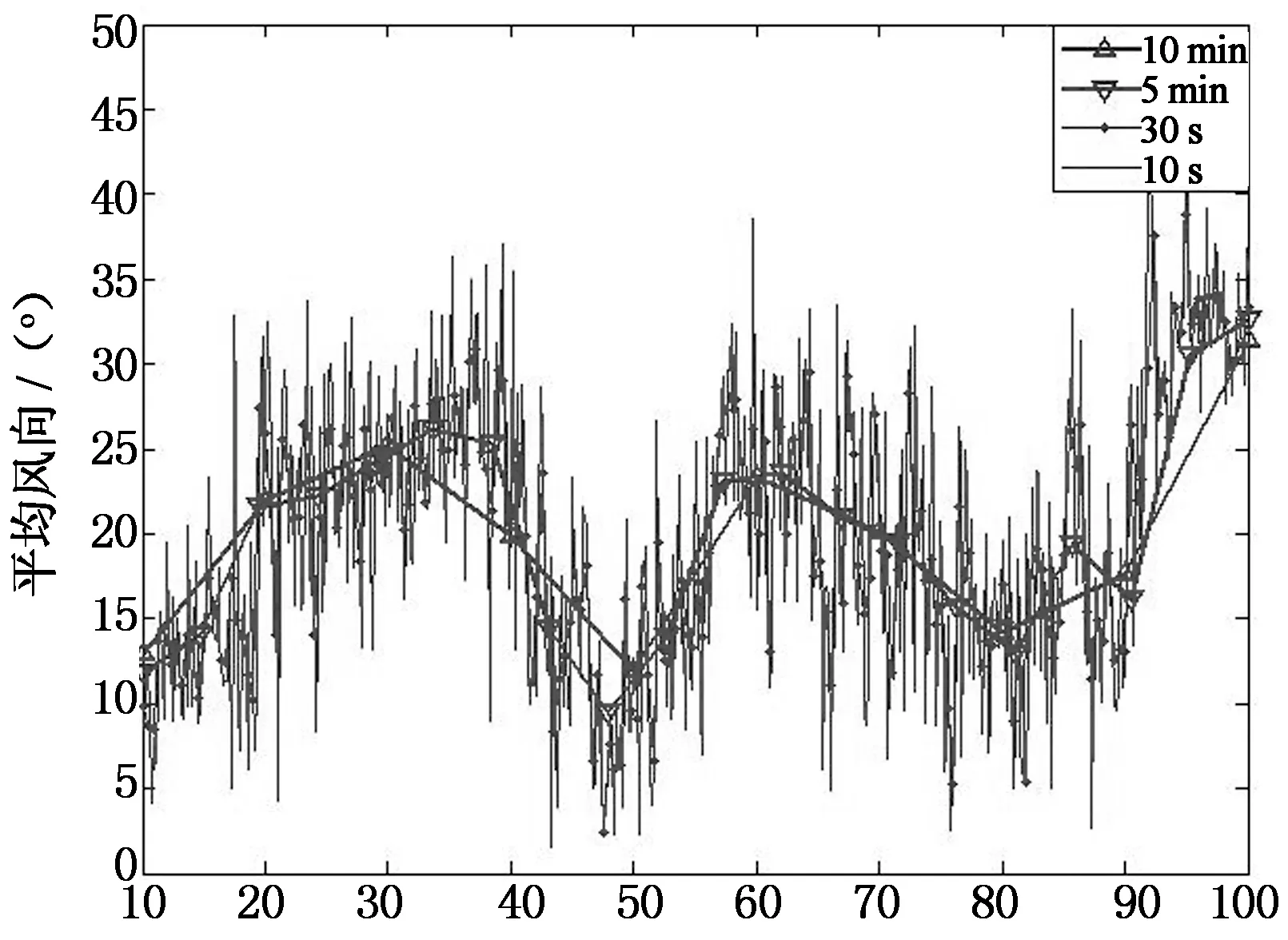
t/min(b)平均风向变化历程图4　平均风速、风向角变化历程Fig.4　Variation of average wind speed, wind direction

2.2脉动风速

在t时距内，顺风向脉动风速u(t)和横风向脉动风速v(t)可根据式(7)，(8)计算：

u(t)=ux(t)cosφ+uy(t)sinφ-u，

(7)

v(t)=-ux(t)sinφ+uy(t)cosφ．

(8)

式中：ux(t),uy(t)的含义及计算方法见2.1节.

以10min为基本时距，选择顺风向和横风向脉动风速均方根值为脉动风速的代表值，脉动风速均方根值σi(i=u,v)定义公式如下：

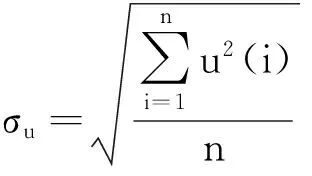
(9)

(10)

其随时间变化历程如图5所示.从图5中可以看出，在100min的脉动风速均方根值的变化历程中，脉动风速均方根值总体呈上升趋势，顺风向和横风向脉动风速均方根值有相似的变化趋势,且顺风向脉动风速均方根值比横风向脉动风速均方根值略大.

2.3湍流度

湍流度反映了风的脉动强度，是确定结构所受脉动风荷载的关键参数.一般而言，湍流度常定义为T时距的脉动风速标准方差与水平平均风速的比值．

(11)

式中：σi分别表示u(t)和v(t)的均方根.

分别以10min,5min,30s,10s为基本时距，计算得到的顺风向和横风向湍流强度随时间变化历程如图6所示，其总的时间长度为100min.从图6可以看出，在该段时间内，湍流度变化趋势大致与脉动风速相似，顺风向湍流强度比横风向略大且变化均随基本时距的增大而更为平缓.若取用其他的时间段时，也可采用相似的方法进行计算分析.

3　实测风压特性

跟风速一样，风压也可以提取一系列代表风压的特征值，如平均风压，脉动风压等.本文以平均风压和脉动风压均方根值作为代表风压的特征值.

该段时间内风主要从东偏北方向吹向实验房，屋盖所在面为东南面和西北面，东南屋盖为背风屋盖，布置测点为W1～W9；西北屋盖为迎风屋盖，布置测点为W10～W18(其中测点W13，W18所测数据无效)．其中，测点W6,W9,W12,和W15受风荷载影响最为明显，所以本文即取这4个测点的风压测值具体分析.由图7屋盖两面各测点的实测风压时程可知，屋盖两面边缘处的各测点均呈现较大的负压.又因为台风影响期间往往伴随着降雨，雨滴对传感器实测风压有些影响，主要表现在雨滴落在传感器表面时可能导致实测风压瞬间大幅变化，在分析平均风压时，因其影响较小，可以忽略不计,但其对瞬时分析结果影响较大.为使分析结果更加准确，本文在分析时均将其作为奇异值剔除.

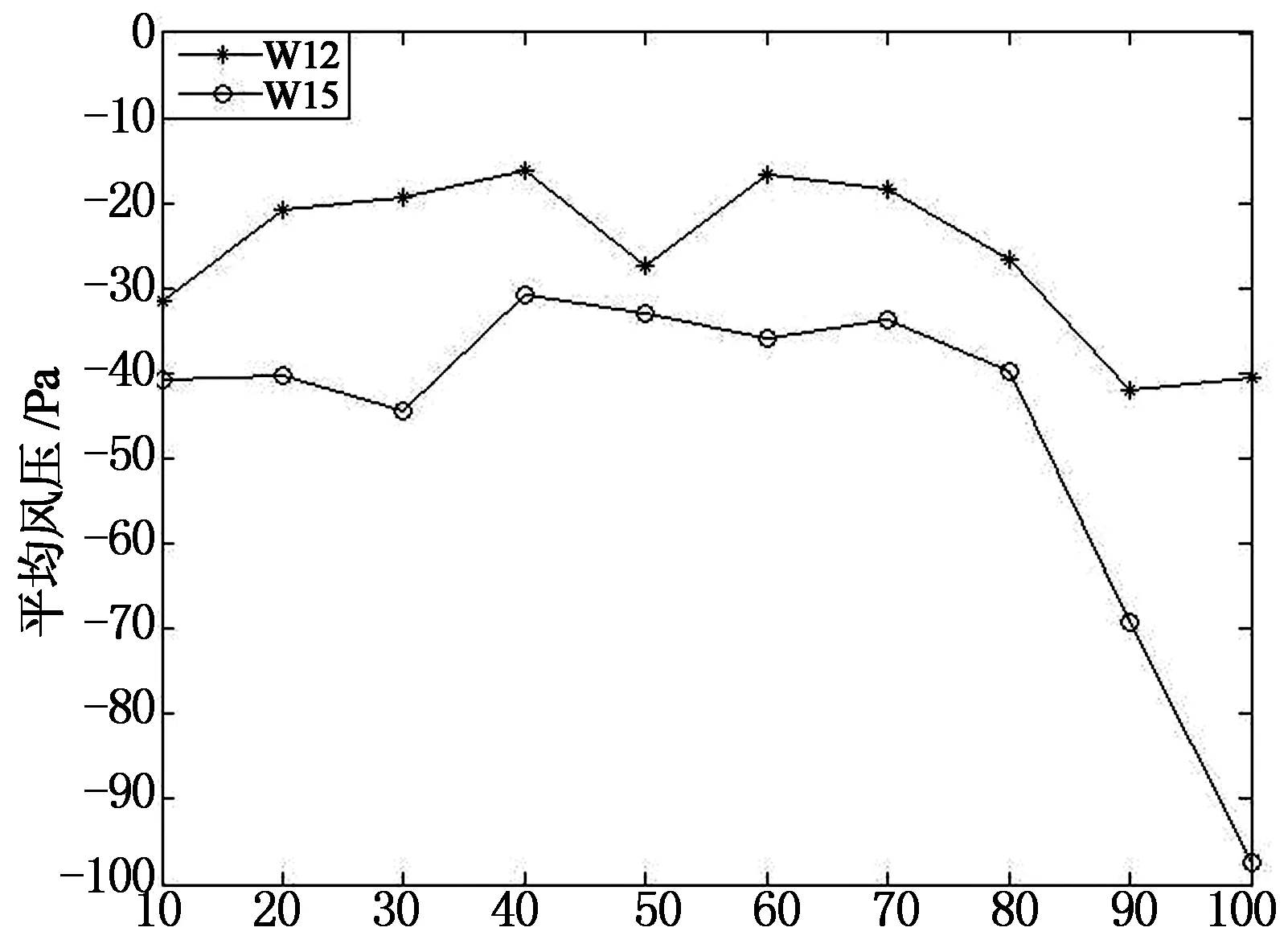
图8，图9所示平均风压和脉动风压均方根值变化历程均为基本时距为10min时计算所得.综合以上屋盖风压变化历程可以看出,当风从角部吹向房屋时，屋盖风压均为较大的负值，脉动风压整体呈上升趋势.

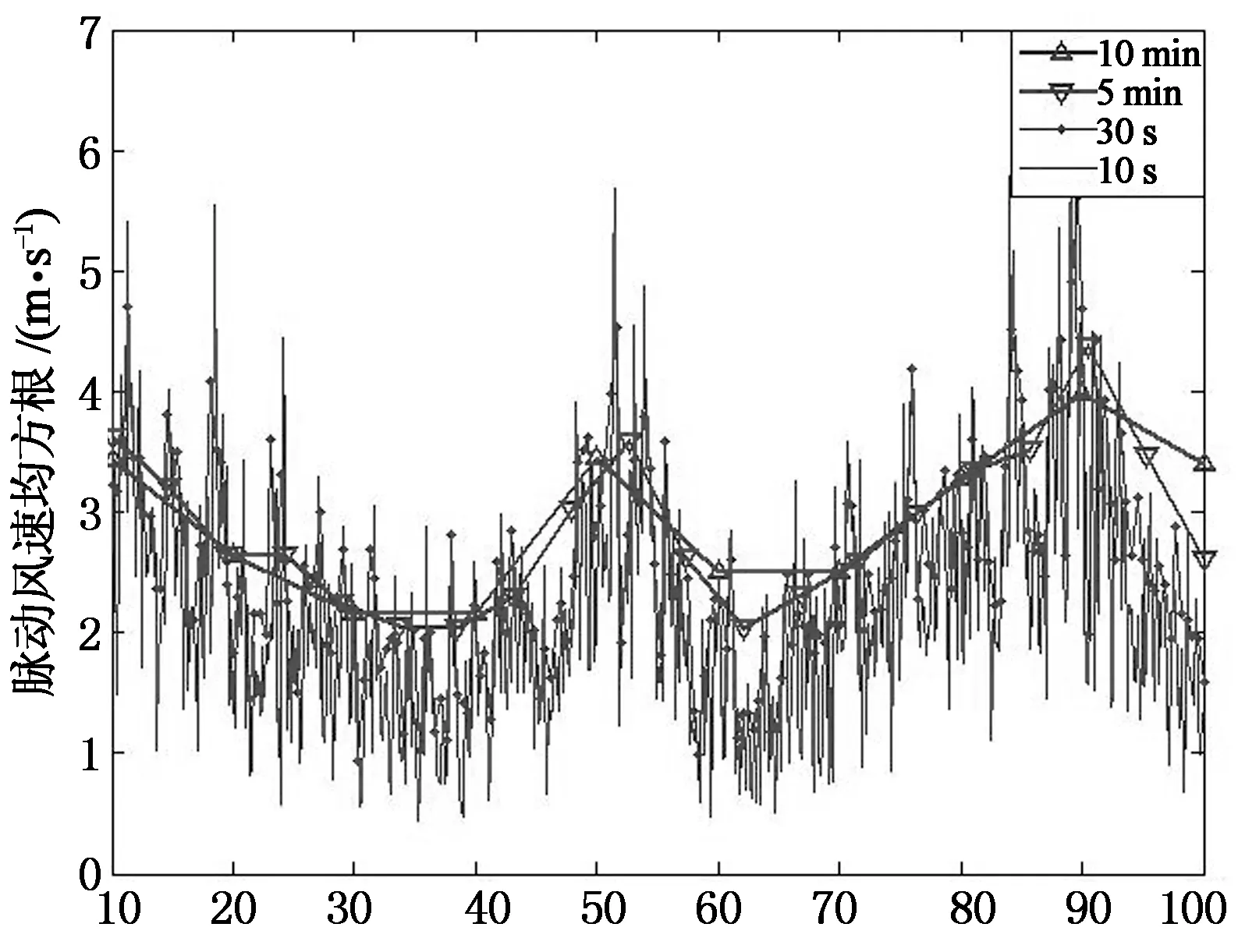
t/min(a)顺风向脉动风速均方根值

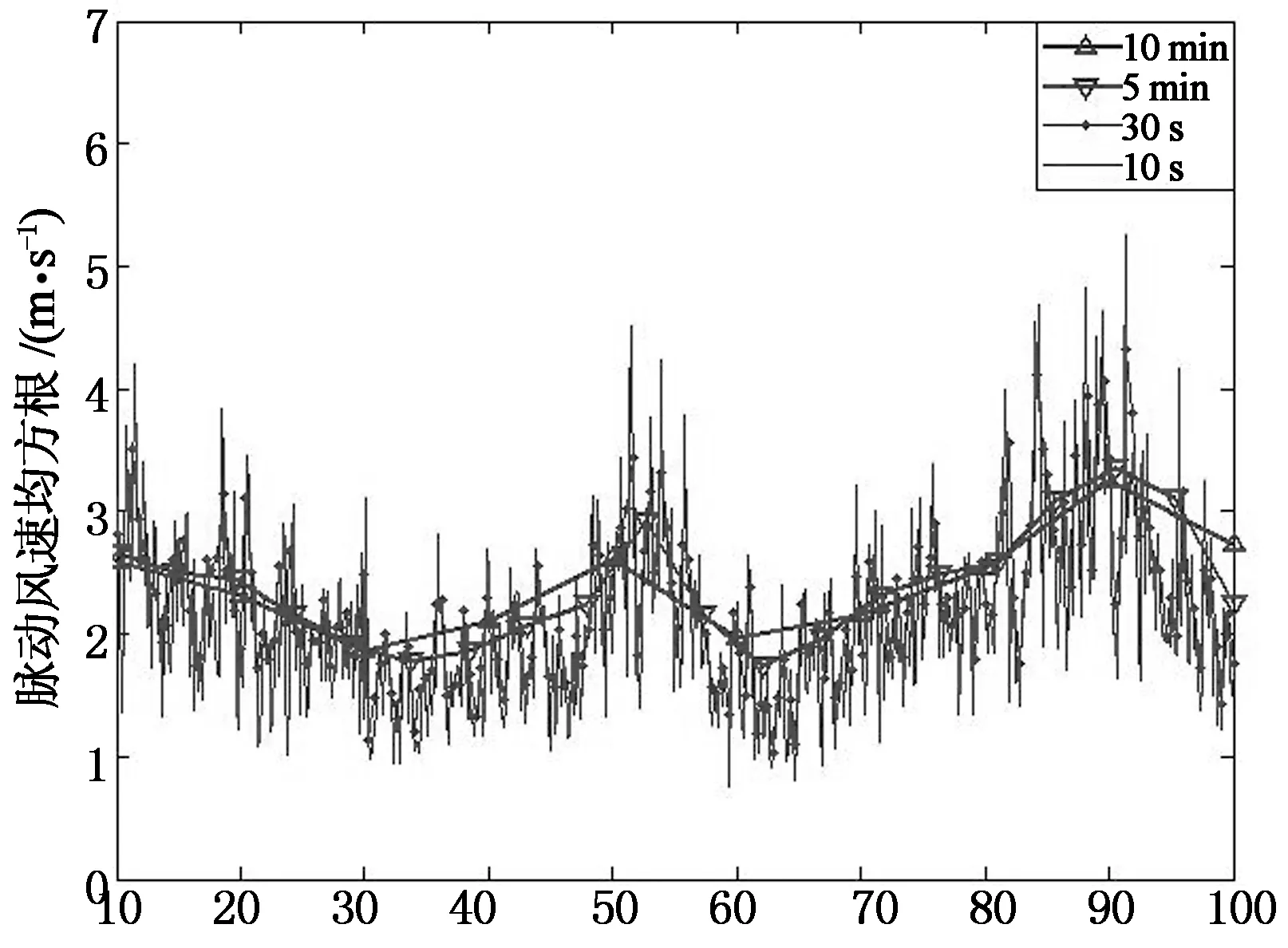
t/min(b)横风向脉动风速均方根值图5　脉动风速均方根值变化历程Fig.5　Variation of root-mean-square value of fluctuating wind speed

t/min(a)顺风向湍流度变化历程

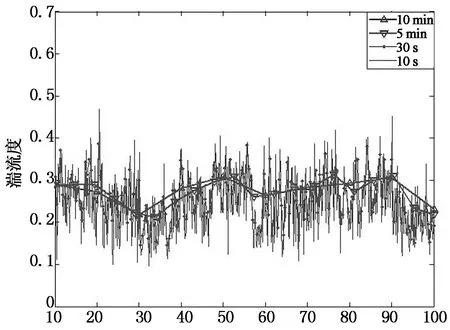
t/min(b)横风向湍流度变化历程图6　湍流度变化历程Fig.6　Variation of turbulence intensity

t/min(a) W6实测风压时程

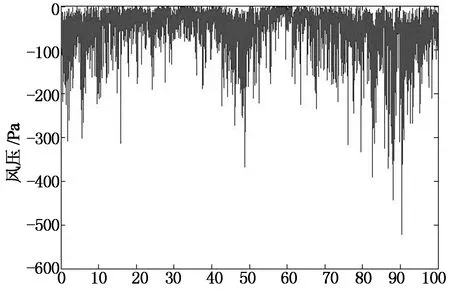
t/min(b) W9实测风压时程

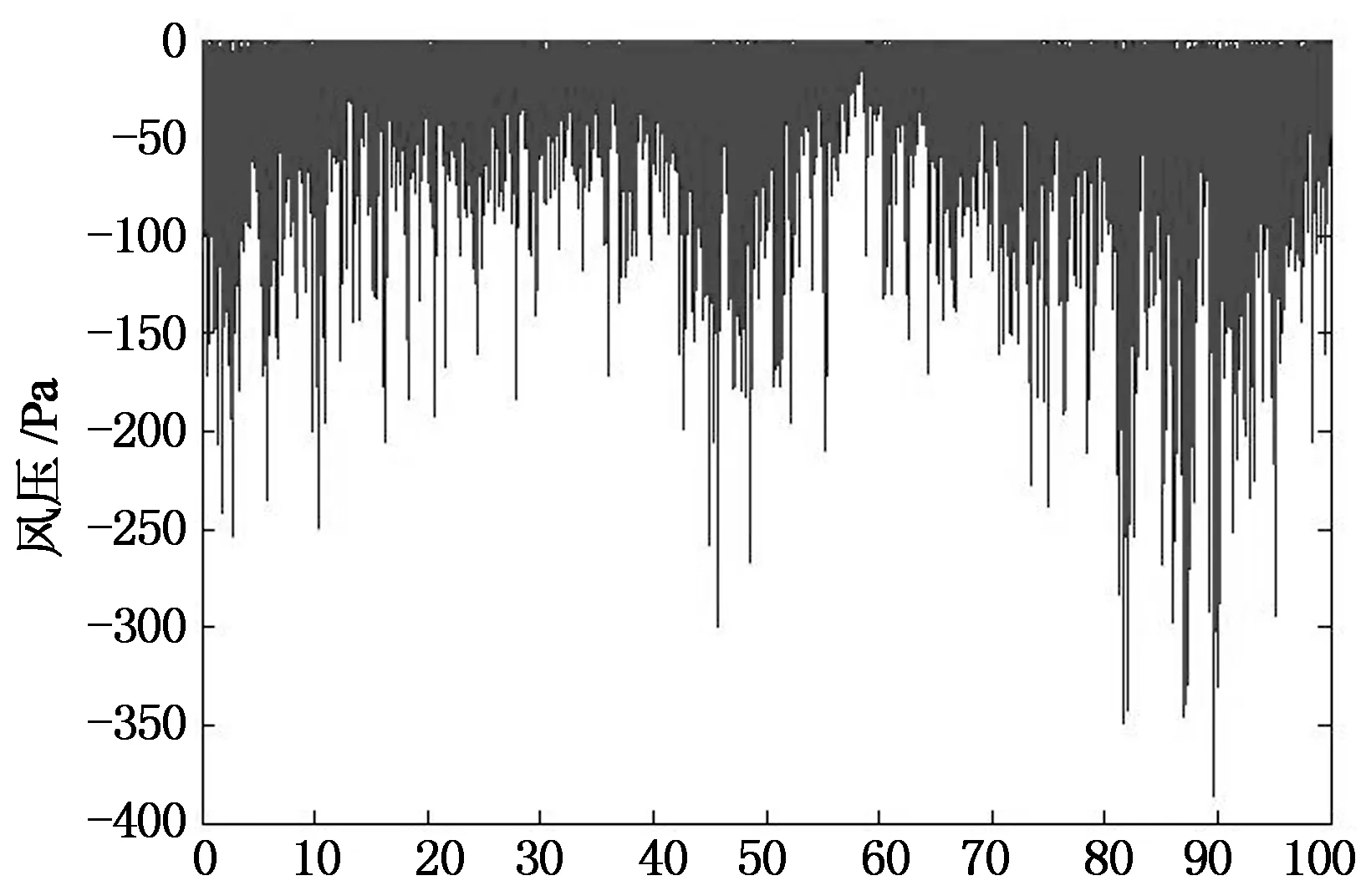
t/min(c) W12实测风压时程

t/min(d) W15实测风压时程图7　 W6,W9,W12和W15实测风压时程Fig.7　Time series of measured wind pressure for W6,W9,W12,W15

t/min(a)平均风压变化历程

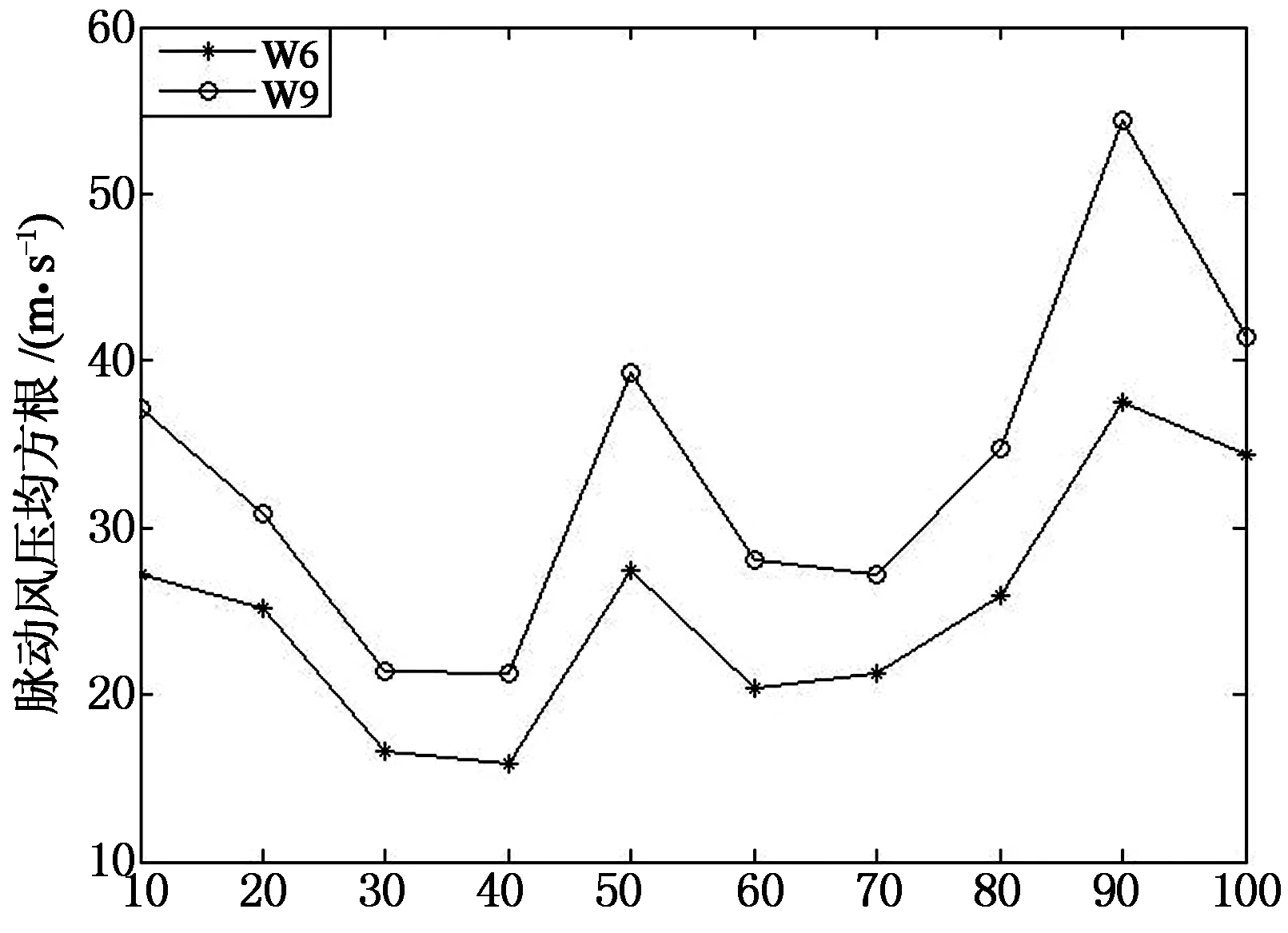
t/min(b)脉动风压均方根值变化历程图8　东南屋盖测点W6，W9平均风压和脉动风压均方根值变化历程Fig.8　Time series of average wind pressure and the root-mean-square value of fluctuatingwind pressure for W6，W9 on the southeast of the roof

t/min(a)平均风压变化历程

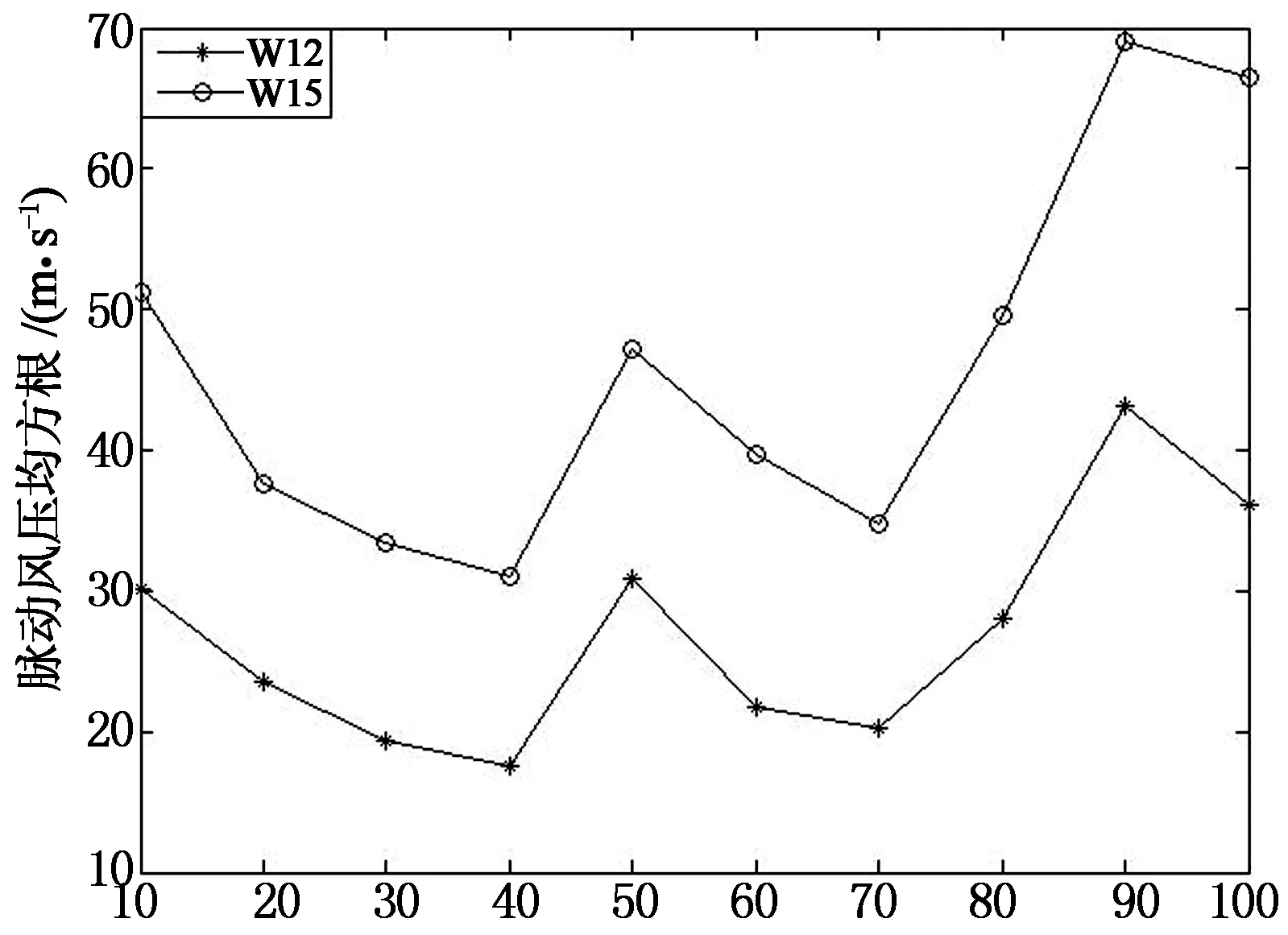
t/min(b)脉动风压均方根值变化历程图9　西北屋盖测点W12，W15平均风压和脉动风压均方根值变化历程Fig.9　Time series of average wind pressure and the root-mean-square value of fluctuating wind pressurefor W12，W15 on the northwest of the roof

4　相关性分析

为了寻找在确定低矮建筑的风压特性和计算体型系数时所适宜的基本时距, 根据前述实测所获得的风场数据和风压场数据,通过相关性分析的方法研究在不同的时距条件下两者之间的相关性，进而确定计算低矮结构的风荷载时最适宜的基本时距.本文采用数理统计和概率论对相关度的定义，求两个符合条件的变量之间的相关性[9].

4.1相关性及其计算

对于一组复杂数据可以使用一定的数学手段生成一个相对简单的类结构，进行“相关性”或 “相似性”分析[10]，最常用的是使用相似系数Cxy来表示指标x和指标y之间的相似关系.Cxy的取值在 -1～1 之间 ,当其绝对值越接近1，表示指标x和指标y之间的关系越密切，当其绝对值越接近0，表示指标x和指标y之间的关系越疏远.对于两条曲线形状变化规律之间的间隔尺度，常用的相似系数有夹角余弦和相关系数.

1)夹角余弦:这是受相似形的启发而来，对于两条曲线，如果长度不一，但是形状相似，当长度不是主要矛盾时，可以定义一种相似系数来表示两条曲线之间的比较密切的相似关系从而加以描述.通常用夹角余弦来描述这种关系，其定义为：

(12)

式中：vkx,vky为所要研究的两个指标向量，在本文研究分析中，vkx分别对应于平均风速和脉动风速均方根值；vky分别对应于平均风压和脉动风压均方根值，k为指标向量的第k个元素，n为指标向量中元素的个数.

2)相关系数:相关系数Cxy就是求将数据标准化 (将指标向量的每个元素减去指标向量元素平均值) 后的夹角余弦.为了简便,在计算分析时,相关系数取计算各指标向量之间的夹角余弦的绝对值.

4.2相关性分析结果

在研究不同时距下，风场与建筑物屋面风压场的相关性的关系时，集中考虑并计算了在不同时距下风速同风压、脉动风速同脉动风压的平均值、最大值、最小值以及均方根值的相关性.计算结果表明，在取用最大值或最小值作为代表值分析时，各时距条件下，相关性系数变化趋势大致相同，但相关性系数普遍较小，所以本文取平均值来分析相关性可能更加合理.

在总的采样时间长度相同，不同平均时距条件下所划分的数据段个数显然是不同的，平均风时距越大所划分的数据段个数越少，而采用上述相关性分析方法，数据段个数的多少直接会影响到计算得到的相关系数值.因此，为了体现最后结果的一般性，分别取等时间长度(取计算总时长为100min)和等数据段个数两种情况进行分析.选取了在时距为1s，2s，3s，5s，10s，0.5min，1min，3min，5min，10min10 个基本时距下的数据进行相关性分析.

1)等时间长度时的相关度

取计算的时间长度为100min，在此条件下，计算得出了在不同时距条件下，平均风速同平均风压以及顺、横方向脉动风速均方根与脉动风压均方根值的相关性.具体计算结果如图10，图11所示.

基本时距/s(a)平均风压和平均风速的相关性

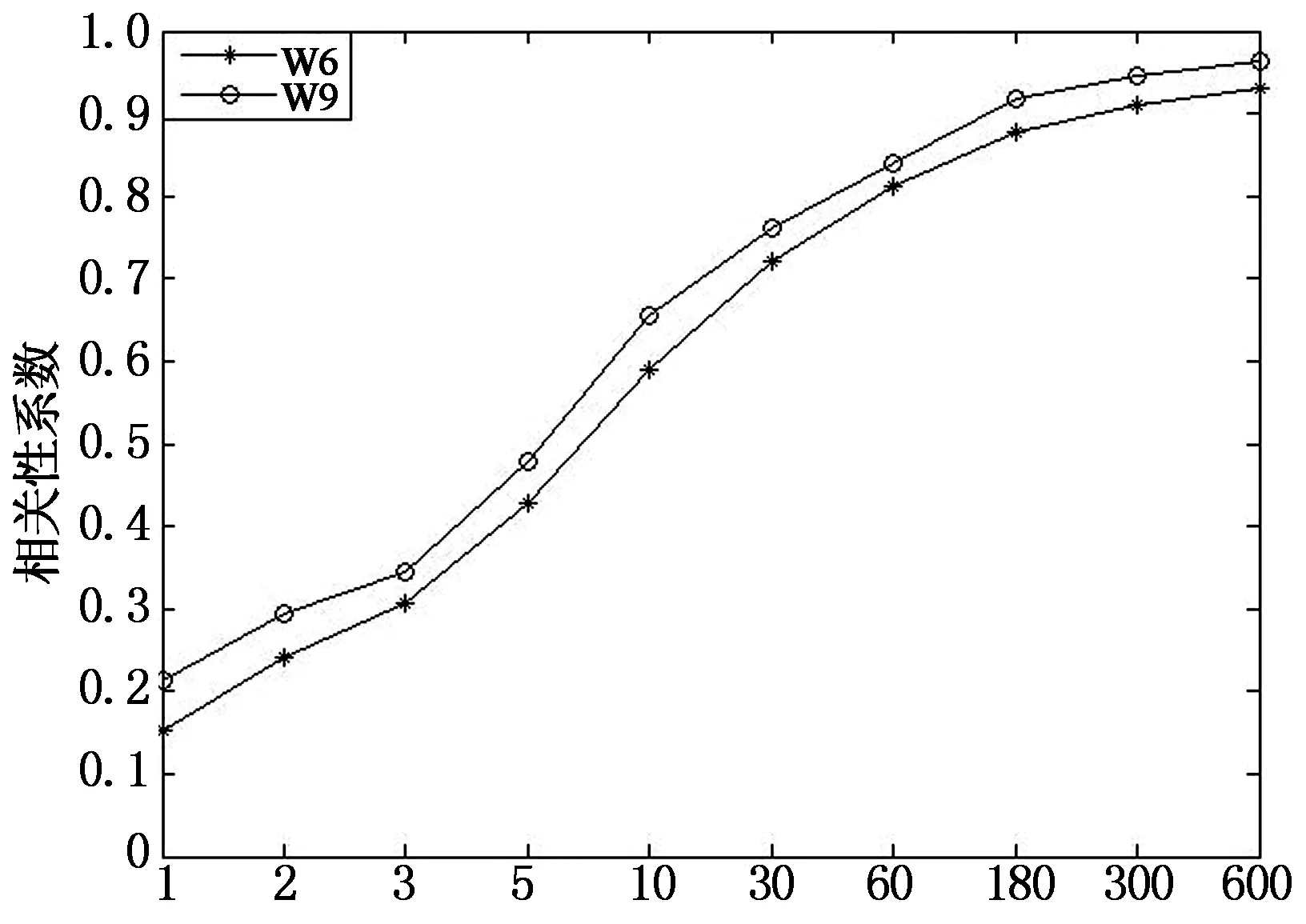
基本时距/s(b)脉动风压均方根和顺风向脉动风速均方根的相关性

基本时距/s(c)脉动风压均方根和横风向脉动风速均方根的相关性图10　东南屋盖风速和风压的相关性Fig.10　Correlation between wind speed andwind pressure on the southeast of the roof

由图10，图11可以看出，随着基本时距的增大，数据段的个数越来越少，风场和风压场各标量之间的相关性系数的值越来越大，当基本时距为1s时相关性非常小，在取基本时距为10min时，相关性系数最大，但在基本时距为3min后相关性系数特别是平均风速与平均风压的相关性系数与之相比差别较小，通过具体分析可以发现，这主要是由参与相关性计算的数据个数不同所引起的，当取计算时间长度为100min时，若取不同的时距计算，则所取的数据个数不同，如假定取基本时距为10min时，则参与计算的数据个数为10个，而取基本时距为1s时，参与计算的数据个数为6 000个.在进行相关性分析时，相关性系数所描述得是两条曲线变化趋势之间的相似性程度，对于每条曲线而言，特征点取得越多，则对曲线的变化趋势描述得越详细，也就越能描述两条曲线的差别.因此在进行相关性系数的计算时，相关性计算结果除与曲线变化趋势有关，还与参与计算的数据个数密切相关.

基本时距/s(a)平均风压和平均风速的相关性

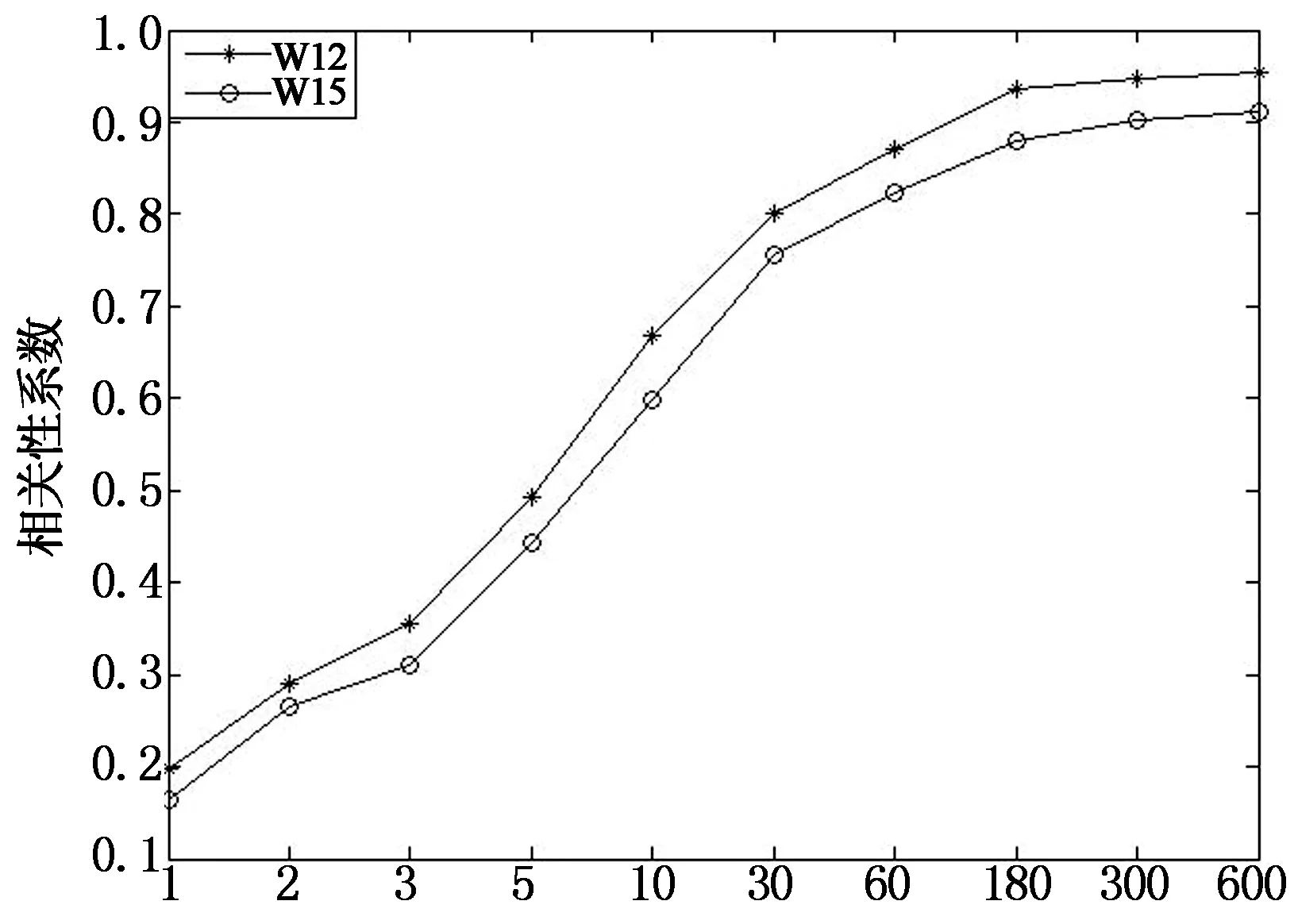
基本时距/s(b)脉动风压均方根和顺风向脉动风速均方根的相关性

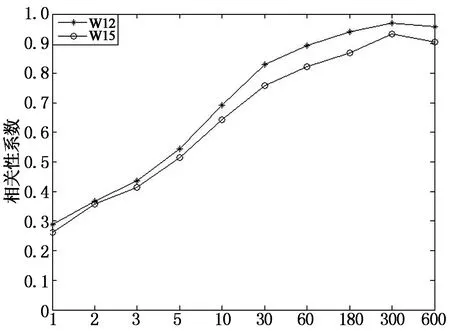
基本时距/s(c)脉动风压均方根和横风向脉动风速均方根的相关性图11　西北屋盖风速和风压的相关性Fig.11　Correlation between wind speed and windpressure on the northwest of the roof

2)等数据个数时相关性结果

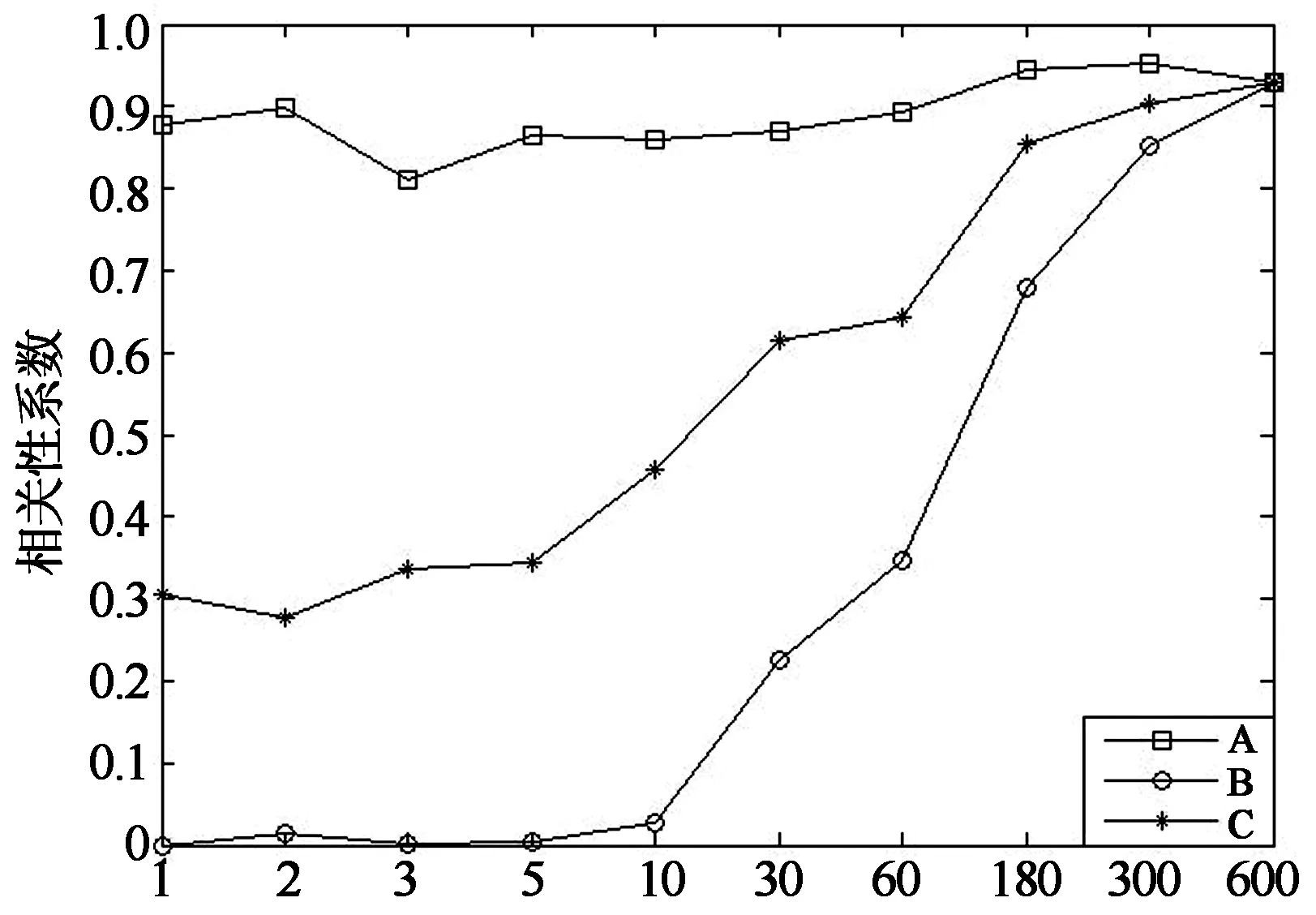
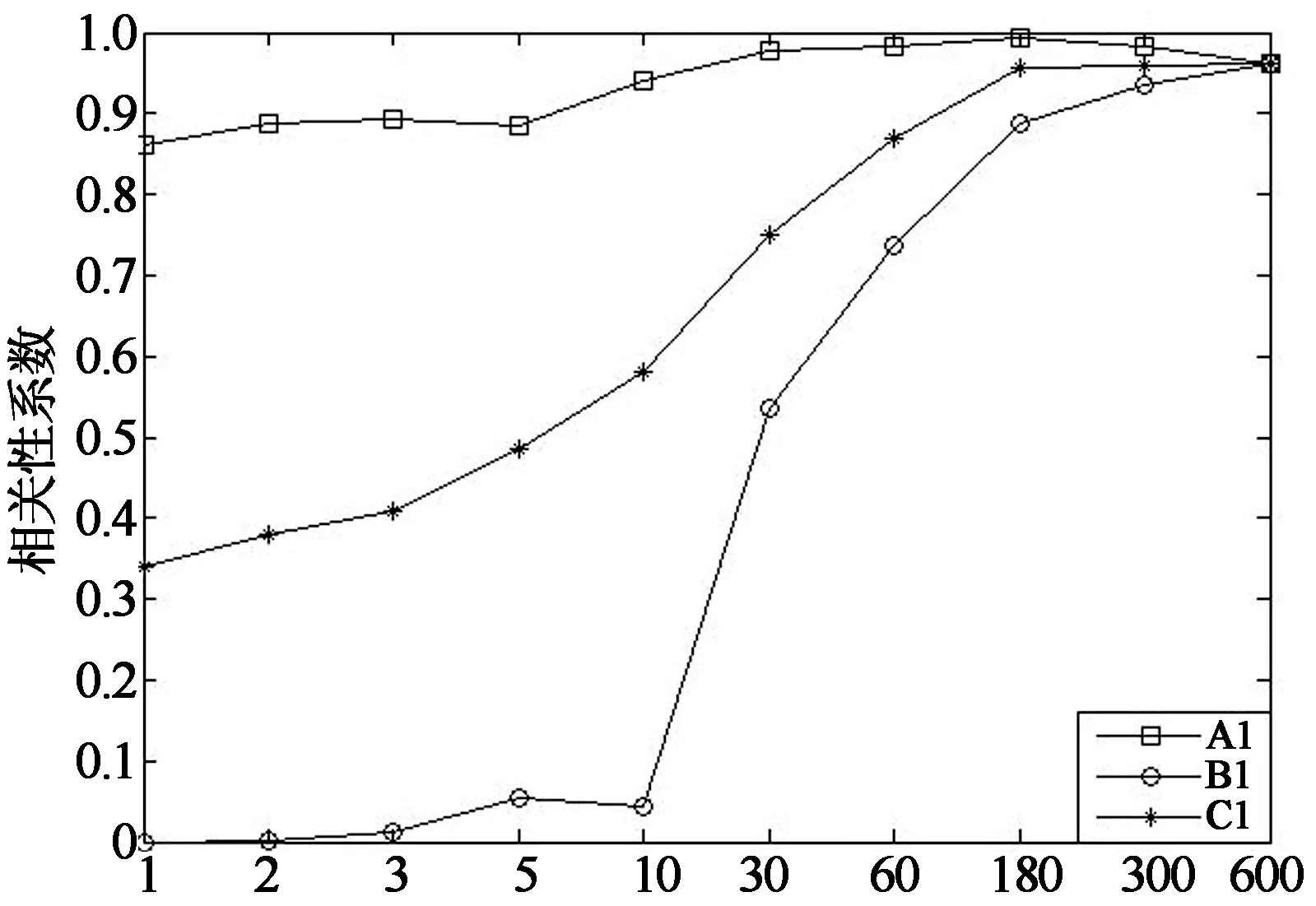
为消除变量个数对计算数学模型的影响，对应不同基本时距取相对应的时间长度，保证在进行相关性系数计算时，在不同的时间间距条件下参与计算的变量数据个数均为10个.例如基本时距为10min时，对应的时间长度为100min，基本时距为1s时，对应的时间长度为10s.进一步考虑到风场数据的脉动性，当基本时距较短时，所取10个数据不能精确地代表所有数据，所以以基本时距为1s时为例，本文计算了100min内测点W6及测点W15全部600个10s数据的相关性，然后就这600个相关性系数的最大值、最小值以及平均值分别与其他时距条件下的相应值进行对比.具体计算结果见图12，图13. 图中,“A”，“B”和“C”分别表示测点W6的相关性系数最大值、最小值以及平均值，“A1～C1”则表示测点W15的相应值.

由图12，图13可以看出，平均风压和平均风速的相关性以及脉动风压均方根和脉动风速均方根的相关性系数变化趋势基本一致.就相关性系数最大值的变化来说，随着基本时距的增大，其变化相对比较平缓，其中基本时距为3min和5min时的相关性系数均比基本时距为10min时的大，且其间差别较小；就相关性系数最小值的变化来说，当基本时距小于10s时，相关性系数近乎为0，当基本时距位于10s～3min时，相关性系数呈现陡增的趋势，当基本时距大于3min时，相关性系数则变化相对平稳，呈小幅递增趋势.西北屋盖的脉动风压均方根和脉动风速均方根的相关性系数变化曲线在基本时距为5min时出现了极值；就相关性系数平均值的变化来说，其变化幅度居于最大值和最小值之间.当基本时距为1s时，相关性系数最小，当基本时距位于1s～3min时，相关性系数呈现稳步递增趋势，当基本时距大于3min时，对于东南屋盖的脉动风压均方根和脉动风速均方根的相关性，相关性系数仍有小幅增加，但变化则相对平缓．对于平均风压和平均风速的相关性以及西北屋盖脉动风压均方根和脉动风速均方根的相关性，相关性系数也有所增加，且均在基本时距为5min时取得了最大值.

综上所述，在进行相关性系数计算时，取相应的不同时间长度保证参与计算相关性系数的数据个数相同时，时距对相关性系数的影响很大，其中，当基本时距为10min和5min时，相关性系数相对较大，且其间差别较小.因为在取较短的时间间距进行分析时，包含更多较大风速的影响，对应于这一时距的最大平均风速将增大[11]，而结构所受风荷载相对而言，较大风速的影响要大一些，所以相对较短的时间间距相关性系数要大一些，且工程结构的风致灾害往往由较大阵风引起，因此取5min为基本时距进行计算更加合理[12-13].

基本时距/s(a)平均风压和平均风速的相关性

基本时距/s(b)脉动风压均方根和顺风向脉动风速均方根的相关性

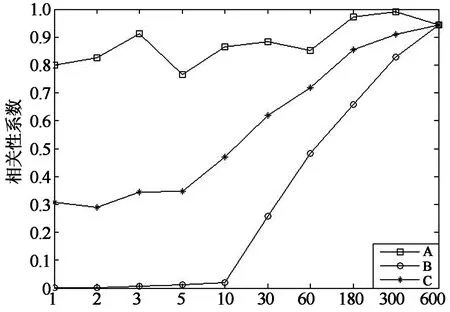
基本时距/s(c)脉动风压均方根和横风向脉动风速均方根的相关性图12　东南屋盖W6测点风速和风压的相关性Fig.12　Correlation between wind speed and windpressure for W6 on the southeast of the roof

基本时距/s(a)平均风压和平均风速的相关性

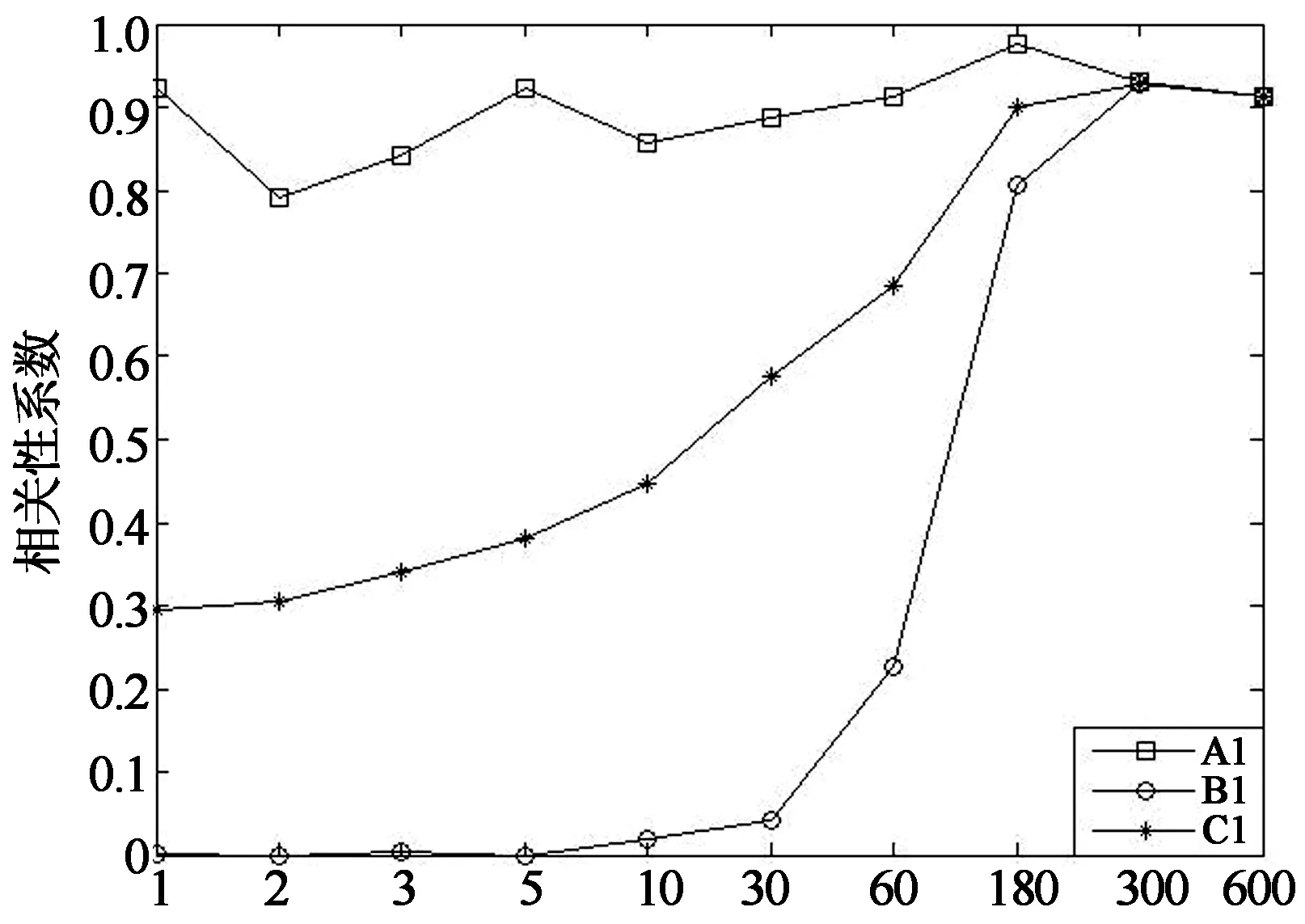
基本时距/s(b)脉动风压均方根和顺风向脉动风速均方根的相关性

基本时距/s(c)脉动风压均方根和横风向脉动风速均方根的相关性图13　西北屋盖W15测点风速和风压的相关性Fig.13　Correlation between wind speed and windpressure for W15 on the northwest of the roof

5　结　论

通过上述对所取时间段内风场和建筑物屋盖风压实测数据及风场参数和风压场参数的相似性分析得到的结果，得出以下结论：

1) 通过对风场特性及风压特性实测数据的分析，风速和风向变化较为平稳；随着平均时距的减小，平均风速最大值增大；湍流度随着平均风速的增大呈逐渐减小的趋势；屋面各测点尤其是西北屋面边缘处的测点W15以及东南屋面屋脊边缘处的测点W9均出现了较大的平均风压和脉动风压.

2)通过对风场参数与风压参数的相关性分析，当取等时长100min进行分析时，由于不同时距条件下，参与分析的数据个数不同，随着基本时距的增大，数据段个数越来越少，所呈现的相关性也越来越大，呈逐步递增趋势，基本时距为10min时，相关性系数最大.

3)取相同的数据个数进行分析时，其中基本时距为5min时，相关性最高.通过对在不同时距条件下相关性系数的最大值、最小值以及平均值的变化趋势进行分析可以看出，在确定风场同风压的相关性时，取5min为基本时距更加合理.

4)综合对相同时间段和相同数据两种情况下的相关性分析,当取基本时距为5min时,风场同风压的相关性较高且比较合理.但是需要指出的是,该结果是根据特定台风下的实测数据分析得出的,在进行相关性分析时取样数据较少,此结论是否具有普遍性有待于进一步研究.

[1]GB50009—2001建筑结构荷载规范[S]．北京:中国建筑工业出版社，2002:30-33.

GB50009—2001Loadcodeforthedesignofbuildingstructures[S]．Beijing:ChinaArchitecture&BuildingPress, 2002: 30-33. (InChinese)

[2]杨庆山, 黄韬颖. 中美澳三国风荷载规范简介及其关于设计风速规定之比较[C]//第十三届全国结构风工程学术会议论文集 (下册).北京：中国土木工程学会, 2007:1110-1118.

YANGQing-shan,HUANGTao-ying.BriefintroductionabouttheloadcodesandcomparisonsbetweendefinitionsaboutdesignedwindspeedinChina,AmericaandAustralia[C] //TheVolumeofEssayoftheThirteenthNationalStructureWindEngineeringConference(Volume2).Beijing:ChinaCivilEngineeringSociety,2007:1110-1118. (InChinese)

[3]LIQS，WUJR，LIANGSG，et al.Full-scalemeasurementsandnumericalevaluationofwind-inducedvibrationofa63-storyreinforcedconcretesupertallbuilding[J].EngineeringStructures,2004,26(12):1779-1794.

[4]黄鹏，戴银桃，王旭，等.华东地区近地台风不同时距特性研究[J].建筑结构学报,2013,34(6):39-45.

HUANGPeng,DAIYin-tao,WANGXu,et al.FieldmeasurementoftyphoonwindsneargroundcharacteristicsatdifferentsegmentlengthsinEastChina[J].JournalofBuildingStructures,2013,34(6):39-45.(InChinese)

[5]UEMATSUY,ISYUMOVN.Windpressuresactingonlowrisebuildings[J].JournalofWindEngineeringandIndustrialAerodynamics, 1999, 82(5):1-25.

[6]MEHTAKC,LEVITANML.Roofcornerpressuresmeasuresinthefieldonalowbuilding[J].JournalofWindEngineeringandIndustrialAerodynamics,1992,41/44(10):181-192.

[7]李秋胜，胡尚瑜，李正农,等. 低矮房屋风荷载实测研究(Ⅱ)——双坡屋面风压特征分析[J].土木工程学报 ,2009, 45(4):1-8.

LIQiu-sheng,HUShang-yu,LIZheng-nong,et al.Fieldmeasurementsofwindloadsonalow-risebuilding——PartⅡ:Windpressuredistributioncharacteristicsongableroof[J].ChinaCivilEngineeringJournal,2009, 45(4)：1-8.(InChinese)

[8]戴益民，李秋胜，李正农，等.低矮房屋屋面风压特性的实测研[J].土木工程学报 2008, 41(6):9-13.

DAIYi-min,LIQiu-sheng,LIZheng-nong,et al.Experimentalstudyofwindpressuresonalow-risefull-scalebuilding[J].ChinaCivilEngineeringJournal,2008, 41(6):9-13.(InChinese)

[9]李正农, 宋克, 李秋胜, 等. 广州中信广场台风特性与结构应的相关性分析[J].实验流体力学, 2009, 23(4): 21-27.

LIZheng-nong,SONGKe,LIQiu-shen，et al.Correlationanalysisofwindcharacteristicandwind-inducedresponseofCITICPlaza[J].JournalofExperimentsinFluidMechanics, 2009,23(4): 21-27.(InChinese)

[10]何晓群. 多元统计分析[M]．3版 . 北京: 中国人民大学出版社，2012:12-17.

HEXiao-qun.Multivariatestatisticalanalysis[M] ．3rded.Beijing:ChinaRenminUniversityPress, 2012:12-17. (InChinese)

[11]张相庭. 结构风工程理论、规范、实践 [M].北京：中国建筑工业出版社, 2005:45-46.

ZHANGXiang-ting.Theory,codeandpracticeofstructuralwindengineering[M].Beijing:ChinaArchitecture&BuildingPress,2005:45-46. (InChinese)

[12]李寿科，李寿英，陈政清，等.大跨屋盖风压场的本征正交分解重构适应性研究[J].湖南大学学报：自然科学版，2011,38(6)：20-26.

LIShou-ke,LIShou-ying,CHENZhen-qing,et al.Properorthogonaldecompositionandreconstructionofwindfieldforlarge-spanroofs[J].JournalofHunanUniversity:NaturalSciences,2011,38(6):20-26．(InChinese)

[13]李秋胜，王云杰，李建成，等.屋盖角部开孔的低矮房屋屋面风载特性研究[J].湖南大学学报：自然科学版，2014,41(6)：1-8.

LIQiu-sheng,WANGYun-jie,LIJian-cheng,et al.Studyofthewindinducedroofpressurecharacteristicsofalow-risebuildingwithholesonitsroofcorner[J].JournalofHunanUniversity:NaturalSciences,2014,41(6):1-8.(InChinese)

Correlation Research of the Measured Wind Field and Wind Pressure of a Low-rise Building

LI Zheng-nong1†, YU Mi1, WU Hong-hua1, SHI Wen-hai2

(1.Key Laboratory of Building Safety and Efficiency of the Ministry of Education, Hunan Univ, Changsha, Hunan410082, China; 2.College of Civil Engineering and Architectural ,Wenzhou Univ, Wenzhou, Zhejiang325035, China)

Thispaperpresentedtheanalysisresultsofthewindfieldcharacteristicsandwindpressureoftheroofonthebasisofthemeasurementdataoftheroofobtainedinaninstrumentedlow-risebuilding,whichsitsinWenzhouandwasaffectedbythetyphoonFitow.Theresultsrevealthat,withthedecreaseoftheaverageinterval,themaximalaveragewindvelocityincreases;theturbulenceintensitytendstodecreasewithanincreasingaveragewindvelocity.Furthermore,theaveragewindpressureattheedgeofthebuildingroofandridgeisnegativewithlargefluctuation.Thevariationtendenciesofwindvelocityandwindpressureshowtheobviouscorrelationbetweenthevelocityinwindfieldandwindpressureontheroof.Thecorrelationanalysisbetweenthewindfieldcharacteristicsandwindpressureontheroofwasthenconductedwithindifferenttimeintervals.Theanalysisresultsshowthatthewindvelocityandwindpressurearecorrelatedwellatanaverageintervalof5minutes,whichindicatesthattheaverageintervalof5minutescanbereasonablyusedtocalculatethewindload.

low-risebuilding;windfield;windpressure;correlation

1674-2974(2016)05-0070-09

2015-06-18

国家自然科学基金资助项目(51278190， 51178180, 51478179，51478366),National Natural Science Foundation of China(51278190， 51178180, 51478179，51478366)

李正农(1962-)，男，湖北武汉人，湖南大学教授，博士生导师

†通讯联系人，E-mail:zhn88@263.net

TU312．1

A